 |
Вычисления с комплексными числами в MathCAD
|
|
|
|
В MathCAD определена мнимая единица j: 
, 
и, следовательно, определены комплексные числа и операции с ними. Для того, чтобы ввести в MathCAD мнимую единицу, следует набрать на клавиатуре < 1 >< j > (в рабочем документе будет отображен символ i, который MathCAD при таком способе ввода воспринимает как мнимую единицу).
Комплексные числа записывают в MathCAD в общепринятой математической нотации. Это означает, что выражение z = a + bj, где а и b – действительные числа, воспринимается как комплексное число, действительная часть которого равна а, а мнимая – b.
В MathCAD можно определять комплексные числа в алгебраической, тригонометрической и показательной форме; однако при символьных вычислениях (с помощью знака символьных преобразований ® или ключевого слова complex) комплексное число все равно отображается в алгебраической форме.
Для вычислений с комплексными числами в MathCAD определены все арифметические операции, а также специфические для комплексной арифметики операции:
u Re(z) – действительная часть комплексного числа z;
u Im(z) – мнимая часть комплексного числа z;
u аrg(z) – главное значение аргумента комплексного числа z;
u 
– модуль 
комплексного числа Z;
u 
= a - jb – число, комплексно сопряженное к числу z.
В MathCAD можно вычислять значения элементарных функций, как действительного, так и комплексного аргумента. Однако при вычислении значений многозначных функций вычисляются только главные значения. Для того, чтобы вычислить все значения многозначных функций, пользователь должен определить их в рабочем документе соответствующими выражениями.
Если уравнение имеет комплексные корни, то MathCAD вычисляет не только действительные, но и комплексные корни.
|
|
|
Расчет электрических цепей с трансформаторами
Уравнения двухобмоточного трансформатора
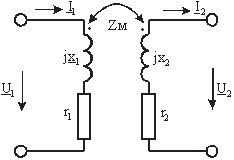
Рис. 3.14
могут быть представлены в виде уравнений четырехполюсника в Z-форме:
(3.26)
При выбранном направлении токов и напряжений
.
Цепь с каскадным соединением трансформаторов
Если известно сопротивление вторичной цепи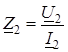 
, можно из второго уравнения (3.26) выразить I 2 через I 1 и таким образом пересчитать сопротивление вторичной цепи в первичную:
. (3.27)
Пересчет сопротивления Z 2 из вторичной цепи в первичную дает возможность при известном напряжении на входе трансформатора определить ток первичной цепи. Для определения тока и напряжения вторичной цепи можно воспользоваться уравнением четырехполюсника в В-форме:
, (3.28)
Литература
1. Теоретические основы электротехники: В 3 т. Учебник для вузов. Том 1, 2. – 4-е изд. / К.С. Демирчян, Л.Р. Нейман, Н.В. Коровкин, В.Л. Чечурин. – СПБ Питер, 2004. – 463, 576 с.
2. Основы теории цепей: Учебник для вузов. Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. – 5-е изд., перераб. – М.: Энергоатомиздат, 1989. – 528 с.
3. К.С. Демирчян, П.А. Бутырин. «Моделирование и машинный расчет электрических цепей». – М.: ВШ., 1988. – 335 с.
4. И. Влах, К. Сингхал. Машинные методы анализа и проектирование электронных схем. – М.: Радиосвязь, 1988. – 560 с.
5. Данилов Л.В. и др. Теория нелинейных электрических цепей (Л.В. Данилов, П.Н. Матханов, Е.С. Филиппов). – Л.: Энергоатомиздат, Ленинград. отд-ие, 1999. – 256 с.
6. Леон О. Чуа и Пен-Мин Лиин. Машинный анализ электронных схем (алгоритмы и вычислительные методы). – М.: Энергия, 1980. – 640 с.
7. Плис А.И., Сливина Н.А. MathCAD. Математический практикум для инженеров и экономистов: учеб. Пособие – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2003. – 656 с.
|
|
|
8. Шабалин В.Д. Машинное моделирование электрических цепей. – Кострома: Изд. Костромской ГСХА, 200. – 80 с.
9. Шабалин В.Д. Пересчет сопротивления нагрузки трехфазной цепи, содержащей трансформатор. / Актуальные проблемы науки в агропромышленном комплексе: материалы 58-й международной научно-практической конференции: в 3 т. Т. 3. – Кострома: КГСХА, 2007. с. 184–185.
|
|
|
