 |
6. Второй закон термодинамики.
|
|
|
|
6. Второй закон термодинамики.
Работоспособность газов
Энтропия
Аналогично внутренней энергии и энтальпии энтропия S является функцией состояния термодинамической системы; это также экстенсивная (аддитивная) величина. Понятие энтропии и второго закона термодинамики, аналитическое выражение которого
dS ³ dQ/T (Дж/К),
неразрывно связаны.
Для обратимых процессов (и только)
dS = dQ/T,
для любого обратимого цикла
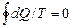(интеграл Клаузиуса),
т. е. dS является полным дифференциалом в отличие от dQ. Подставляя в (4. 1) и (4. 2) dq=Tds (Дж/кг) в удельных (массовых) величинах, получаем (s – удельная энтропия, Дж/(кг. К))
dh=Tds+vdP, du=Tds–Pdv (Дж/кг). (6. 1)
Каждое из этих уравнений является аналитическим выражением объединенных первого и второго законов термодинамики для обратимых процессов.
Идеальный газ (Pv=RT, du=cvdT, dh=cpdT, cp–cv=R). В этом случае из уравнений (6. 1) следует (Ds =s2 – s1)
ds=cvdT/T+Rdv/v, ® Ds=cvln(T2/T1)+Rln(v2/v1), (6. 2)
ds=cpdT/T–RdP/P, ® Ds=cpln(T2/T1)–Rln(P2/P1), (6. 3)
ds=cvdP/P+cp dv/v, ® Ds=cv ln(P2/P1) + cp ln(v2/v1). (6. 4)
а). Изохорный процесс (v=const), dq=cvdT.
ds=cvdT/T ® Ds=cv ln(T2/T1)= cv ln(P2/P1).
б). Изобарный процесс (P=const), dq=cpdT.
ds=cpdT/T ® Ds=cp ln(T2/T1)= cp ln(v2/v1).
в). Изотермический процесс (T=const), du=cvdT=dh= cpdT=0.
T=Pv/R; dq=Pdv=–vdP, ds=Rdv/v=–RdP/P,
® Ds=R ln(v2/v1)= R ln(P1/P2).
г). Адиабатный процесс (dq=0), ds=0(для обратимых процессов) Ds=0, s=const® изоэнтропийный процесс.
д). Политропный процесс (dq=cп dT, cп =const),
ds=cпdT/T ® Ds=cп ln(T2/T1)= cv(n–k)/(n–1) ln(T2/T1).
Для этого процесса T2/T1=(v1/v2)n–1=(P2/P1)(n–1)/n.
Замечание 1. Аддитивна энтропия S системы, удельная энтропия s – неаддитивная (интенсивная) величина, как и все удельные величины.
Пример. Два изолированных объема жидкости массой M1 и М2 разделены адиабатной (нетеплопроводной) перегородкой. Жидкости имеют одно и то же давление и температуры T1 и T2 соответственно. Определить изменение энтропии DS этой системы после того, как перегородка убирается и жидкости смешиваются. Жидкость считать несжимаемой, теплоемкости с1 и с2 заданы и постоянны.
|
|
|
Решение
а). Температура, которая установится в системе (Tсм – температура смешения), определяется из уравнений теплового баланса
с1M1(Tсм–T1)=DQ1, с2M2(Tсм–T2)=DQ2, DQ1+DQ2=0.
Решение этих уравнений: Tсм=(с1M1T1 + с2M2T2) / (с1M1+ с2M2).
б). Для каждой жидкости dq=cdT и ds=cdT/T. Отсюда
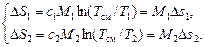
В силу экстенсивности энтропии (полной, а не удельной) из этих равенств окончательно получаем
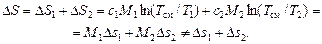
Замечание 2. Следует иметь в виду, что табличные значения внутренней энергии, энтальпии, энтропии (uт, hт, sт), представленные в таблицах теплофизических свойств и соответствующих диаграммах состояния для различных веществ, в действительности представляют собой их приращения (Dh, Du, Ds) относительно некоторого характерного для этого вещества (одного из многих) термодинамического состояния (P0, V0, T0).
Например,
hт(P1, V1, T1)= h(P1, V1, T)– h0(P0, V0, T0)
и, очевидно,
Dh= h(P2, V2, T2)– h(P1, V1, T1)= hт(P1, V1, T1)= Dhт.
Для воды обычно полагают, что uт = hт = sт =0 в «тройной точке». Иногда полагают, что uт = hт = sт =0 при нормальных физических условиях. Для каждого вещества нулевые точки разные, и здесь всегда требуется уточнение.
Эксергия рабочего тела
Под эксергией рабочего тела (ex) понимают максимальную полезную работу (работоспособность), которую можно получить от изолированной системы, состоящей из рабочего тела (источник работы) и окружающей среды, имеющей заданные фиксированные значения давления P0 и температуры T0. Для рабочего тела
ex=(u–u0)–T0(s–s0)+P0(v–v0) (Дж/кг), (6. 5)
где u, s, v – удельные внутренняя энергия, энтропия и объем рабочего тела в начальном неравновесном с окружающей средой состоянии; u0 , s0, v0 – те же величины в конечном равновесном с окружающей средой состоянии.
|
|
|
Эксергия потока вещества (рабочего тела)
ex=(h–h0)–T0(s–s0) (Дж/кг), (6. 6)
где h=u+Pv – энтальпия. Для идеального газа du=cvdT, dh=cpdT.
Эксергия теплоты. Максимальное количество полезной работы, которую можно получить в термодинамическом цикле за счет теплоты, сообщаемой рабочему телу горячим источником Q1, при заданных температурах горячего T1 и холодного T2 < T1 источников теплоты Q2, называется эксергией (работоспособностью) теплоты. Ее величина определяется по формуле
ех = Q1(1–T2/T1) = Q1ht ,
где ht – термический к. п. д. цикла Карно.
|
|
|
