 |
Задачи. 4. Первый закон термодинамики
|
|
|
|
Задачи
3. 1. Смесь 10 кг кислорода и 15 кг азота имеет давление 0, 3 МПа и температуру 27º C. Определить мольные доли zi каждого газа в смеси, кажущуюся молярную массу смеси, газовую постоянную, общий объем смеси, парциальные давления и объемы газов.
3. 2. Определить газовую постоянную смеси газов, состоящей из 1 м3 генераторного газа и 1, 5 м3 воздуха, взятых при нормальных физических условиях, и найти парциальные давления составляющих смеси. Плотность генераторного газа принять равной 1, 2 кг/м3.
3. 3. Газ коксовых печей имеет следующий объемный состав: H2=57%, CH4=23%, СО=6%, CO2=2%, N2=12%. Определить кажущуюся молярную массу смеси, массовые доли составляющий смеси, газовую постоянную, плотность смеси, парциальные давления газов при 15º C и 1 бар.
3. 4. Воздух объемом 0, 3 м3 смешивается с 0, 5 кг углекислого газа. Оба газа до смешения имели параметры P=0, 6 МПа, t=45º C. Определить парциальное давление углекислого газа после смешения.
3. 5. Определить удельный объем пара натрия при P=1 МПа, t=927º C, если известно, что при этих параметрах пар натрия является смесью одноатомных и двухатомных молекул мольного состава: r(Na)= 0, 8628, r(Na2)=0, 1372. Найти парциальные давления одно- и двухатомных паров натрия. Вычислить, как велика была бы ошибка в значении удельного объема, если бы пар натрия считался одноатомным. Молярная масса μ =23 кг/кмоль.
3. 6. В энергетических установках, работающие по парогазовому циклу, в качестве рабочего тела используется смесь водяного пара и горячих продуктов сгорания топлива. Массовая доля продуктов сгорания g=0, 7. Принять, что продукты сгорания обладают свойствами воздуха. Определить теплоемкость смеси cp при температуре 500 и 800º C, а также удельный объем смеси при P=0, 1 МПа и t=500º C.
|
|
|
3. 7. В сосуде находится смесь газов, образовавшаяся в результате смешения 10 кг азота, 13 кг аргона и 27 кг двуокиси углерода. Определить мольный состав смеси, ее удельный объем при нормальных условиях, кажущуюся молярную массу смеси и газовую постоянную, отнесенную к 1 м3 при нормальных условиях.
3. 8. Влажный воздух представляет собой смесь сухого воздуха и перегретого водяного пара. Известно, что на каждый килограмм сухого воздуха во влажном воздухе приходится d граммов водяного пара. Определить массовые и объемные доли сухого воздуха и водяного пара, плотность при нормальных условиях, газовую постоянную и кажущуюся молярную массу смеси, если d=10 г/кг сухого воздуха.
3. 9. Смесь газов, образовавшаяся при сжигании 1 кг мазута в топке парового котла, имеет состав, определенный парциальными объемами составляющих V(CO2)=1, 85 м3, V(O2)=0, 77 м3, V(N2)=12, 78 м3. Определить массовые доли и парциальные давления составляющих, если общее давление P=1 бар.
3. 10. Сосуд разделен перегородкой на две части, объемы которых V1=1, 5 м3, V2=1, 0 м3. В части объемом V1 содержится двуокись углерода при P1=0, 5 МПа и t1=30º C, а в части объемом V2 – кислород при P2=0, 2 МПа и t2=57º C. Определить массовые и объемные доли двуокиси углерода и кислорода, кажущуюся молярную массу смеси и ее газовую постоянную после того, как перегородка будет убрана и процесс смешения закончится.
3. 11. Горючий газ, полученный при подземной газификации угля, имеет следующий объемный состав: N2=63, 6%, H2=14, 5%, СО=10, 0%, СO2=9, 5%, H2S=0, 6%, CH4=1, 8%. Рассчитать приведенный к нормальным условиям объем воздуха, теоретически необходимый для сгорания 1 м3 газа, взятого также при нормальных условиях.
3. 12. 2 м3 воздуха при давлении 5 бар и температуре 50º C смешивается с 10 м3 воздуха при давлении 2 бар и температуре 100 º C. Определить давление и температуру смеси.
|
|
|
3. 13. В двух разобщенных между собой сосудах A и B содержатся следующие газы: в сосуде А – 50 л азота при P1 = 20 бар и t1 = 200º C; в сосуде В – 200 л углекислого газа при P2 = 5 бар и t2 = 600º C. Определить давление и температуру, которые установятся после соединения сосудов. Теплообменом с окружающей средой пренебречь.
3. 14. Три разобщенных между собой сосуда A, B, C заполнены различными газами. В сосуде А, имеющем объем 10 л, находится сернистый ангидрид SO2 при давлении 60 бар и температуре 100º C, в сосуде B объемом 5 л – азот при давлении 4 бар и температуре 200º C и в сосуде C объемом 5 л – азот при давлении 2 МПа и температуре 300º C. Определить давление и температуру, которые установятся после соединения сосудов между собой. Считать, что теплообмен со средой отсутствует.
3. 15. В сборном газоходе котельной смешиваются уходящие газы трех котлов, имеющих атмосферное давление. Для упрощения принимается, что эти газы имеют одинаковый массовый состав, а именно: CO2=11, 8%, O2=6, 8%, N2=75, 6%, H2O=5, 8%. Часовые расходы газов составляют Q1=7100 м3/ч, Q2=2600 м3/ч, Q3=11200 м3/ч, а температуры газов соответственно равны t1=170º C, t2=220º C, t3=120º C. Определить температуру газов после смешения и их объемный расход через дымовую трубу при этой температуре.
3. 16. Определить средние объемную, мольную и массовую теплоемкости для смеси газов, состоящих из CO2 – 9%, CO – 1%, N2 – 81%, O2 – 9%. Давление смеси равно 1, 5 бар, а температура 560º F.
3. 17. Определить парциальное давление кислорода, находящегося в смеси следующего объемного состава: Ar – 25%, CO2 – 39%, O2 – 36%. Смесь находится под давлением 1, 5 атм при температуре 275º R. Определить также плотность смеси.
3. 18. В первом сосуде объемом 5 м3 содержится смесь газов N2 – 81%, O2 – 19%, давление в сосуде равно 15 МПа. Во втором сосуде объемом 150 л содержится He при температуре 137º C и давлении 10 МПа. Определить, какое давление и температура установятся в системе из двух сосудов, если их соединить между собой.
4. Первый закон термодинамики
Подведенная к телу теплота Q расходуется на увеличение его внутренней энергии U и на совершение работы L. В дифференциальной форме уравнение первого закона (начала) термодинамики (в отсутствие обмена веществом) имеет вид
|
|
|
dQ = dU + dL.
Правило знаков. Теплота, подведенная к телу, считается положительной, а отведенная – отрицательной. Работа, произведенная телом, считается положительной, а работа, совершенная над телом, – отрицательной.
В СИ единицей измерения энергии является Джоуль (Дж = Н·м). Теплота и работа как формы передачи энергии имеют ту же единицу измерения.
Внутренняя энергия является функцией состояния. Ее изменение в ходе любого термодинамического процесса, переводящего тело (термодинамическую систему) из одного равновесного состояния в другое равновесное состояние, определяется лишь ее значениями в начальном и конечном состояниях, т. е. DU = U2–U1. Это означает, что dU является полным дифференциалом (dQ и dL таким свойством не обладают). Энергия – величина экстенсивная (аддитивная), т. е. энергия системы равна сумме энергий составляющих частей системы.
В случае, когда тело совершает работу только против сил внешнего давления, dL = PdV (работа расширения). Соответственно, уравнение первого закона термодинамики для удельных (массовых) величин с учетом правила знаков имеет вид
du = dq – Pdv. (4. 1)
Здесь u=U/M (Дж/кг), q=Q/M (Дж/кг), v=V/M (м3/кг).
Энтальпия H=U+PV (Дж) так же, как и внутренняя энергия, является функцией состояния, т. к. P, V – параметры состояния. Поскольку du=dh–Pdv–vdP, уравнение первого закона в удельных величинах может быть записано в форме
dh = dq + vdP (Дж/кг). (4. 2)
Произведение vdP называется располагаемой работой.
Идеальный газ. Согласно закону Джоуля внутренняя энергия идеального газа зависит только от температуры. Так как для идеального газа Pv=RT, то этим свойством обладает и энтальпия идеального газа. Прямым следствием закона Джоуля являются равенства
(Дж/кг).
сv, cp (Дж/кг K) – удельные теплоемкости в процессах подвода тепла при постоянном объеме и постоянном давлении соответственно.
|
|
|
Таким образом, для идеального газа уравнения (4. 1) и (4. 2) имеют вид
(4. 3)
Вычитая из первого уравнения второе, получим для удельных массовых теплоемкостей
(Дж/(кг K))
и, т. к. R=R0/m,
(формула Р. Майера).
Отсюда для удельных молярных (мольных) теплоемкостей
(Дж/кмоль K).
Удельная объемная теплоемкость для газов (с*) приводится к объему при нормальных физических условиях (Vн):
с*=μ с/22, 41 (Дж/м3 с)
и
сp*– сv*=R0/22, 41 (Дж/м3 K).
Для каждого вещества значения теплоемкостей определяются экспериментально и представлены в справочной литературе. Для оценочных расчетов можно принимать значения молярных теплоемкостей для разреженных газов (кДж/кмоль K), приведенные в табл. 4. 1.
Таблица 4. 1
| Газ | 
| 
| – теория
|
| Одноатомный | 12, 56 | 20, 93 |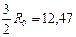 
|
| Двухатомный | 20, 93 | 29, 31 |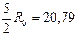 
|
| Трехатомный | 29, 31 | 37, 68 | 
|
Следует различать истинную и среднюю теплоемкости.
По определению истинная теплоемкость c=dq/dT. Это функция температуры и процесса. Средняя теплоемкость связана с температурным интервалом: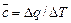 
, 
. Очевидно,
что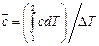 
. Подведенное тепло (энергия в форме тепла) рассчитывается обычно с использованием средних значений теплоемкостей:
.
Обычно знак усреднения (черта) опускается при использовании этих формул.
Замечание 1. С целью унификации таблиц и диаграмм принято считать, что внутренняя энергия равна нулю в «тройной» точке воды:
P = 610, 8 Па; T = 273, 16К=0, 01º C; v = 0, 0010002 м3/кг.
В этой точке h = 0, 611 Дж/кг.
Замечание 2. В силу исторических причин в энергетике также используется (вне системы единиц СИ) как единица энергии калория:
международная – 1 кал =4, 1868 Дж;
15-градусная – 1 кал=4, 1858 Дж;
термохимическая – 1 кал = 4, 1840 Дж.
Иногда энергию измеряют в «лошадиных силах в час»:
1 л. с. ч = 75 кгс·м/с·3600 с = 75·9, 8065 Н·м/c·3600 с ≈ 2648 кДж.
1 л. с. ≈ 736 Дж/с = 736 Вт.
|
|
|
