3. Смеси идеальных газов. Уравнение состояния отдельной компоненты газа в смеси. Уравнение состояния смеси. Теплоемкость смеси идеальных газов

3. Смеси идеальных газов

 

Физической моделью идеального газа, приводящей к уравнению Менделеева - Клапейрона, является система материальных точек, взаимодействующих только путем упругих соударений; другие механизмы взаимодействия отсутствуют. В отсутствие химического взаимодействия смесь одноатомных или многоатомных идеальных газов также является идеальным газом, для которого справедливо уравнение Менделеева-Клапейрона.

 

Уравнение состояния отдельной компоненты газа в смеси

Ввиду отсутствия сил взаимодействия каждый газ «не чувствует» присутствия других компонент смеси и занимает весь объем сосуда (V_см). В силу термодинамической равновесности температура (T) компонент и смеси одна и та же. Следовательно, давление (P_j), оказываемое на стенки сосуда только j-й компонентой k-компонентной смеси, определяется из уравнения

                    (3. 1)

Здесь n_j – количество киломолей  j-й компоненты в смеси. Эти давления называют парциальными.

Уравнение состояния смеси

В соответствии с законом Дальтона (закон парциальных давлений) полное давление рассматриваемой смеси газов равно сумме парциальных давлений:

.

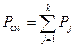Суммируя отдельно левые и правые части уравнений (3. 1) по j, получим

Здесь  – масса смеси; M_j/M_см=g_j – массовая доля j-й компоненты в смеси. Это и есть уравнение состояния смеси идеальных газов (Менделеева-Клапейрона). С учетом закона Дальтона оно имеет вид

 – эффективная или кажущаяся молярная масса газовой смеси.

Вне смеси любой газ при заданном давлении и температуре смеси (P_см, T) занимал бы объем V_j, определяемый из уравнения

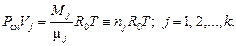                          (3. 2)

Эти условные для смеси объемы называют парциальными объемами. Из уравнений (3. 1), (3. 2) ввиду равенства их правых частей следует, что

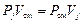 или .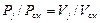

Суммируя это уравнение по j, с учетом закона Дальтона получаем

.

Эффективную молярную массу смеси можно рассчитать, если известны объемные доли компонентов смеси r_i=V_j/V_см. Перепишем уравнение (3. 2) в виде

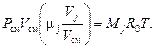
Суммируя по j левые и правые части этого уравнения, с учетом вида уравнения состояния газовой смеси находим

.

Замечание 1. Выше было получено, что . Из уравнения (3. 1) и уравнения состояния смеси следует, что , т. е. объемные и молярные (n_j / n) доли совпадают:

.

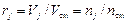Замечание 2. Реальными величинами газовой смеси являются количества молекул каждой компоненты смеси (N_j). Общее количество молекул смеси . Поскольку каждый киломоль любого вещества по определению содержит одно и то же число молекул (N_A), то общее число киломолей в смеси равно сумме киломолей компонент смеси (n_j):

.

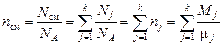По определению μ _см:

a)

б)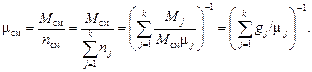

Теплоемкость смеси идеальных газов

Удельная теплоемкость вещества определяется как теплоемкость:

а) единицы его массы (кг) – массовая удельная теплоемкость, с_m [Дж/(кг·K)];

б) единицы его количества (кмоль) – молярная (мольная) удельная теплоемкость, с_μ [Дж/(кмоль·K)];

в) единицы его объема (м³) – объемная удельная теплоемкость, с* [Дж/(м³·K)].

Для смеси идеальных газов или любой другой ее компоненты, имеющей массу M (кг), содержащей n киломолей и занимающей объем V (м³), изменение количества тепла DQ и соответствующее изменение температуры DT связаны уравнениями (с_m, с_μ , с* – средние значения)

DQ= с_m·M·DT= с_μ ·n·DT= с*·V_н·DT.

Здесь V_н – объем, который занимает газ массой M при нормальных физических условиях: P₀=101325 Па, T₀=273, 15 К. Отсюда получаем соотношения:

Для смеси 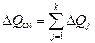, следовательно,

,

,

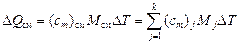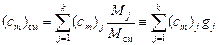Если смесь задана объемными долями, то

и

Здесь V_j – парциальные объемы.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: