 |
Модуль 1. Вероятностное пространство с не более чем счетным множеством элементарных исходов
|
|
|
|
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственное образовательное учреждение
Высшего профессионального образования
«Южный Федеральный университет»
Факультет математики, механики и компьютерных наук
УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС
Учебной дисциплины
«Теория вероятностей и математическая статистика»
Для бакалавров
Вузовского компонентного цикла ОПД
По специальности 010501
«Прикладная математика и информатика»
Рассмотрено и рекомендовано УТВЕРЖДАЮ
на заседании кафедры Декан факультета
теории функций и
функционального анализа ЮФУ
Протокол №____ _________________
«___»________2008 г.
«___»________2008 г.
Зав кафедрой ____________ (Кондаков В.П.)
Составитель:
Доцент кафедры Луценко А.И.
Ростов-на-Дону
2008
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
I. Цели и задачи дисциплины, ее место в учебном процессе
I.1 Цели преподавания дисциплины
Курс «Теория вероятностей и математическая статистика» - общеобразовательная математическая дисциплина, объектом изучения которой является большая область математики, связанная понятиями случайности событий, измерением степени возможности появления этих событий, проведением экспериментальных исследований и математической обработкой их результатов, формулировкой полученных результатов.
Курс «Теория вероятностей и математическая статистика» читается студентам специальности “прикладная математика и информатика” в VI и VII семестрах. Цель преподавания – ознакомить студентов с задачами и методами теории вероятностей и математической статистики в объёме, достаточном для успешного практического использования полученных знаний в дальнейшей работе по специальности, а также для самостоятельного изучения соответствующей научной литературы.
|
|
|
I.2 Задачи изучения дисциплины
В результате изучения настоящего курса студент должен:
1) овладеть основами теории вероятностей, усвоив понятия множества элементарных исходов, алгебры случайных событий, вероятностной функции как числовой функции множеств, случайной величины, функции распределения случайной величины и числовых характеристик случайной величины;
2) ознакомится с методами и результатами решения классической предельной проблемы теории вероятностей, а также с применением этих результатов к решению задач статистической оценки значений числовых характеристик случайных величин и векторов и статистической проверки гипотез, построению простейших регрессионных моделей;
3) приобрести навыки практического решения вероятностных задач, постановки задач проведения статистического эксперимента, научится приёмам и методам статистической обработки экспериментальных данных и формулированию обоснованных выводов по результатам этой обработки.
I.3 Перечень дисциплин с указанием разделов (тем), знание которых необходимо для изучения теории вероятностей и математической статистики
1) Элементы теории множеств (операции над множествами, конечные и бесконечные множества, сравнение бесконечных множеств по мощности, алгебра множеств);
2) Математический анализ (теория пределов, непрерывные и дифференцируемые функции, ряды, преобразование Фурье);
3) Теория функций и функциональный анализ (понятия меры и измеримости множеств, интеграла Лебега, гильбертова пространства, различных видов сходимости последовательностей).
Согласно государственного образовательного стандарта высшего профессионального образования от 14 апреля 2000 года на изучение дисциплины «Теория вероятностей и математическая статистика» отведено 280 часов (70 часов лекционных + 35 часов практических аудиторных занятий + 175 часов самостоятельной работы) и предусмотрены следующие формы отчётности: 1 экзамен, 1 зачёт, 3 контрольных работы и 1 зачётное индивидуальное задание по математической статистике.
|
|
|
II. Рабочая программа курса
Модуль 1. Вероятностное пространство с не более чем счетным множеством элементарных исходов
Основные понятия: Элементарный исход. Множество элементарных исходов. Алгебра событий. Вероятностная функция. Условная вероятность.
Вероятностное пространство < W, A, P >
| Множество элементарных исходов W | Алгебра событий A | Вероятностная функция P |
| Примеры | Операции над событиями | Простейшие свойства |
1. Классическая модель:  ;
;
(Урновая схема, различные способы организации выборок).
2. Биномиальная модель (Схема Бернулли): 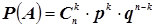 ;
;
(Полиномиальная модель).
3. Геометрическая модель:  ;
;
(Отрицательное биномиальное распределение).
Условная вероятность. Попарная независимость событий и независимость событий в совокупности.
Формула полной вероятности. Формула Байеса. (7 часов)
|
|
|


