 |
VI. Индивидуальные задания по математической статистике
|
|
|
|
Методические указания
Для лучшего усвоения приёмов и методов математической статистики каждый студент получает индивидуальное задание.
Это задание представляет собой наборы статистических данных, полученных экспериментальным путём, и являются выборками значений двумерных случайных величин. В ходе выполнения работы студент должен выполнить следующие пять заданий, соответствующим пяти модулям теоретического курса.
Первичная обработка статистических данных.
Необходимо построить вариационные ряды. Построить гистограммы. Определить значения точечных оценок числовых характеристик случайных величин.
Интервальные оценки числовых характеристик случайных величин.
Построение доверительных интервалов для математических ожиданий и дисперсий. Приобретение навыков работы с таблицами специальных распределений математической статистики.
Статистическая проверка гипотез.
Решаются три задачи. Проверка гипотез о равенстве значений числовых характеристик некоторому фиксированному числу. Проверка гипотез о совпадении значений одноимённых числовых характеристик двух случайных величин.
Проверка гипотезы о виде закона распределения исследуемой случайной величины.
Критерий «согласия» Пирсона. Проверка гипотезы о совпадении законов распределения двух случайных величин.
Корреляционный анализ.
Оценка силы статистической связи между случайными величинами. Определение методом наименьших квадратов статистических оценок коэффициентов функции регрессии. Построение соответствующей геометрической иллюстрации.
Все задания выполняются последовательно по мере накопления теоретического материала. Студент представляет для зачёта каждое выполненное задание. Выполнение заданий предполагает использование персонального компьютера. Все задания представляются в распечатанном виде. После получения зачёта выполненные задания остаются у студента и могут в дальнейшем быть использованы как руководства по математической обработке статистических материалов.
|
|
|
Образцы статистических данных для выполнения индивидуальных заданий
Вариант № образец
Двумерная случайная величина дискретного типа
Длина слова (выборки  и
и 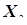 ) и количество гласных в этом слове (выборки
) и количество гласных в этом слове (выборки 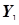 и
и 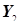 ) в орфографическом словаре русского языка.
) в орфографическом словаре русского языка.
| № | 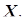
| 
| 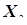
| 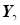
| № | 
| 
| 
| 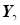
|
| 1 | 6 | 3 | 4 | 2 | 51 | 9 | 3 | 7 | 3 |
| 2 | 16 | 7 | 7 | 3 | 52 | 8 | 3 | 8 | 3 |
| 3 | 4 | 2 | 9 | 4 | 53 | 9 | 3 | 6 | 2 |
| 4 | 8 | 4 | 7 | 3 | 54 | 9 | 3 | 8 | 4 |
| 5 | 5 | 2 | 6 | 2 | 55 | 11 | 5 | 7 | 2 |
| 6 | 9 | 3 | 6 | 2 | 56 | 15 | 7 | 8 | 2 |
| 7 | 12 | 6 | 7 | 3 | 57 | 8 | 2 | 3 | 1 |
| 8 | 11 | 6 | 8 | 3 | 58 | 10 | 4 | 7 | 3 |
| 9 | 9 | 5 | 6 | 3 | 59 | 6 | 2 | 9 | 4 |
| 10 | 7 | 3 | 5 | 3 | 60 | 7 | 2 | 7 | 3 |
| 11 | 8 | 3 | 7 | 3 | 61 | 8 | 3 | 7 | 3 |
| 12 | 8 | 4 | 7 | 3 | 62 | 6 | 4 | 11 | 5 |
| 13 | 6 | 3 | 5 | 2 | 63 | 5 | 2 | 9 | 4 |
| 14 | 9 | 5 | 8 | 3 | 64 | 7 | 3 | 7 | 3 |
| 15 | 5 | 2 | 5 | 2 | 65 | 5 | 2 | 7 | 3 |
| 16 | 7 | 4 | 12 | 4 | 66 | 5 | 2 | 6 | 2 |
| 17 | 10 | 6 | 5 | 2 | 67 | 7 | 2 | 8 | 3 |
| 18 | 9 | 4 | 5 | 2 | 68 | 9 | 5 | 8 | 3 |
| 19 | 10 | 5 | 8 | 3 | 69 | 7 | 3 | 9 | 5 |
| 20 | 14 | 7 | 9 | 3 | 70 | 5 | 2 | 6 | 3 |
| 21 | 12 | 5 | 5 | 2 | 71 | 8 | 3 | 7 | 3 |
| 22 | 7 | 3 | 7 | 3 | 72 | 7 | 3 | 6 | 2 |
| 23 | 7 | 3 | 5 | 2 | 73 | 10 | 5 | 5 | 2 |
| 24 | 6 | 3 | 3 | 1 | 74 | 8 | 4 | 8 | 3 |
| 25 | 7 | 4 | 4 | 2 | 75 | 8 | 3 | 8 | 4 |
| 26 | 12 | 6 | 7 | 2 | 76 | 8 | 3 | 5 | 2 |
| 27 | 12 | 6 | 8 | 3 | 77 | 5 | 2 | 12 | 4 |
| 28 | 8 | 5 | 5 | 2 | 78 | 12 | 5 | 11 | 6 |
| 29 | 9 | 4 | 7 | 3 | 79 | 15 | 6 | 5 | 2 |
| 30 | 7 | 3 | 5 | 2 | 80 | 9 | 4 | 6 | 2 |
| 31 | 12 | 7 | 3 | 1 | 81 | 7 | 3 | 4 | 1 |
| 32 | 7 | 3 | 6 | 2 | 82 | 8 | 4 | 7 | 3 |
| 33 | 8 | 4 | 6 | 2 | 83 | 10 | 4 | 7 | 2 |
| 34 | 5 | 2 | 7 | 3 | 84 | 4 | 2 | 10 | 4 |
| 35 | 8 | 3 | 8 | 3 | 85 | 9 | 4 | 6 | 2 |
| 36 | 7 | 4 | 5 | 2 | 86 | 6 | 4 | 14 | 7 |
| 37 | 11 | 5 | 8 | 3 | 87 | 5 | 2 | 12 | 5 |
| 38 | 6 | 3 | 6 | 2 | 88 | 5 | 2 | 8 | 3 |
| 39 | 5 | 2 | 6 | 2 | 89 | 6 | 2 | 8 | 3 |
| 40 | 7 | 3 | 9 | 3 | 90 | 10 | 4 | 5 | 2 |
| 41 | 9 | 4 | 7 | 2 | 91 | 5 | 3 | 7 | 3 |
| 42 | 5 | 2 | 3 | 1 | 92 | 8 | 5 | 5 | 2 |
| 43 | 6 | 2 | 8 | 3 | 93 | 17 | 8 | 6 | 2 |
| 44 | 10 | 4 | 10 | 4 | 94 | 18 | 7 | 15 | 7 |
| 45 | 10 | 4 | 7 | 4 | 95 | 7 | 5 | 10 | 4 |
| 46 | 7 | 3 | 5 | 2 | 96 | 7 | 4 | 10 | 4 |
| 47 | 17 | 9 | 7 | 4 | 97 | 5 | 3 | 8 | 4 |
| 48 | 10 | 4 | 5 | 2 | 98 | 6 | 3 | 6 | 3 |
| 49 | 10 | 4 | 10 | 4 | 99 | 10 | 5 | 6 | 2 |
| 50 | 9 | 5 | 7 | 3 | 100 | 7 | 4 | 11 | 3 |
|
|
|
Вариант № образец
Двумерная случайная величина непрерывного типа
Рост (см) (выборки  и
и 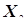 ) и Длина окружности грудной клетки (см) (выборки
) и Длина окружности грудной клетки (см) (выборки  и
и  ) двух групп обследованных юношей-призывников.
) двух групп обследованных юношей-призывников.
| № | 
| 
| 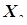
| 
| № | 
| 
| 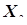
| 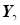
|
| 1 | 157,5 | 84,0 | 159,5 | 85,0 | 51 | 162,5 | 87,5 | 170,0 | 88,5 |
| 2 | 165,0 | 89,5 | 169,5 | 88,0 | 52 | 168,0 | 86,5 | 161,5 | 87,5 |
| 3 | 160,0 | 82,5 | 155,5 | 81,5 | 53 | 157,0 | 80,5 | 166,5 | 88,0 |
| 4 | 164,0 | 85,0 | 164,5 | 88,5 | 54 | 163,5 | 90,0 | 154,0 | 80,0 |
| 5 | 162,0 | 84,5 | 173,0 | 83,5 | 55 | 160,5 | 87,0 | 168,5 | 83,0 |
| 6 | 165,5 | 85,0 | 158,5 | 86,5 | 56 | 169,5 | 86,5 | 162,5 | 89,0 |
| 7 | 169,5 | 87,0 | 173,5 | 91,5 | 57 | 166,5 | 84,0 | 165,0 | 86,0 |
| 8 | 155,5 | 78,0 | 165,5 | 81,5 | 58 | 164,0 | 87,0 | 160,0 | 84,0 |
| 9 | 172,5 | 83,5 | 161,5 | 78,0 | 59 | 175,0 | 83,5 | 177,0 | 90,0 |
| 10 | 163,0 | 83,0 | 166,5 | 89,5 | 60 | 158,0 | 84,5 | 164,0 | 87,5 |
| 11 | 158,5 | 83,0 | 152,0 | 81,5 | 61 | 162,0 | 88,0 | 174,5 | 90,0 |
| 12 | 166,0 | 90,0 | 166,0 | 87,0 | 62 | 158,5 | 89,5 | 158,5 | 81,5 |
| 13 | 168,5 | 91,5 | 163,0 | 84,5 | 63 | 174,5 | 88,5 | 166,0 | 90,0 |
| 14 | 161,0 | 80,0 | 167,0 | 86,5 | 64 | 166,5 | 88,0 | 167,0 | 88,5 |
| 15 | 167,0 | 84,5 | 157,5 | 79,5 | 65 | 163,0 | 86,0 | 160,0 | 81,5 |
| 16 | 153,0 | 79,5 | 167,5 | 81,0 | 66 | 165,5 | 83,5 | 168,5 | 85,5 |
| 17 | 164,5 | 79,0 | 162,0 | 79,5 | 67 | 170,5 | 86,0 | 162,5 | 83,5 |
| 18 | 165,5 | 88,5 | 164,5 | 79,0 | 68 | 160,0 | 86,0 | 163,5 | 91,5 |
| 19 | 160,0 | 88,0 | 169,0 | 87,0 | 69 | 163,5 | 80,5 | 167,5 | 85,0 |
| 20 | 167,5 | 79,5 | 160,5 | 81,0 | 70 | 176,5 | 87,5 | 157,0 | 85,5 |
| 21 | 162,5 | 79,0 | 170,5 | 81,5 | 71 | 154,5 | 85,0 | 172,5 | 92,0 |
| 22 | 171,0 | 85,5 | 162,5 | 85,0 | 72 | 172,0 | 91,5 | 164,5 | 88,0 |
| 23 | 158,0 | 77,5 | 164,0 | 93,0 | 73 | 162,5 | 83,5 | 160,0 | 90,0 |
| 24 | 168,0 | 89,0 | 171,5 | 85,0 | 74 | 169,0 | 85,5 | 175,0 | 89,5 |
| 25 | 163,5 | 84,5 | 153,5 | 79,5 | 75 | 156,5 | 82,0 | 166,0 | 86,0 |
| 26 | 170,0 | 91,0 | 170,5 | 91,0 | 76 | 164,0 | 86,0 | 161,0 | 86,0 |
| 27 | 161,0 | 80,5 | 165,5 | 83,5 | 77 | 168,0 | 85,0 | 170,5 | 83,5 |
| 28 | 172,5 | 89,5 | 163,0 | 83,5 | 78 | 159,5 | 84,5 | 162,5 | 82,5 |
| 29 | 162,0 | 85,0 | 163,0 | 84,0 | 79 | 165,0 | 81,5 | 174,5 | 87,5 |
| 30 | 164,0 | 91,5 | 166,5 | 91,5 | 80 | 171,0 | 83,5 | 161,0 | 86,5 |
| 31 | 156,0 | 78,5 | 158,0 | 83,0 | 81 | 161,0 | 79,5 | 167,5 | 84,5 |
| 32 | 165,0 | 86,5 | 165,0 | 86,5 | 82 | 174,0 | 87,0 | 165,0 | 81,0 |
| 33 | 169,0 | 93,5 | 168,0 | 90,0 | 83 | 158,5 | 87,5 | 153,0 | 83,5 |
| 34 | 160,0 | 83,0 | 169,5 | 84,5 | 84 | 166,0 | 81,5 | 169,0 | 93,5 |
| 35 | 164,5 | 77,5 | 164,5 | 89,0 | 85 | 169,5 | 87,0 | 163,5 | 89,5 |
| 36 | 173,0 | 85,5 | 169,0 | 81,5 | 86 | 162,5 | 89,5 | 162,0 | 80,0 |
| 37 | 154,0 | 79,5 | 156,0 | 82,0 | 87 | 172,5 | 86,5 | 161,0 | 82,0 |
| 38 | 167,0 | 87,5 | 167,0 | 84,0 | 88 | 152,0 | 84,0 | 167,0 | 85,0 |
| 39 | 161,5 | 80,5 | 163,5 | 87 | 89 | 168,5 | 83,0 | 171,0 | 85,5 |
| 40 | 168,5 | 81,5 | 169,5 | 90,5 | 90 | 160,5 | 83,5 | 156,5 | 83,5 |
| 41 | 165,5 | 79,5 | 157,5 | 86,5 | 91 | 157,5 | 80,0 | 164,5 | 81,5 |
| 42 | 169,0 | 80,5 | 171,0 | 89,0 | 92 | 170,5 | 87,5 | 169,0 | 86,5 |
| 43 | 166,0 | 85,5 | 161,5 | 80,5 | 93 | 162,0 | 84,0 | 159,5 | 82,5 |
| 44 | 170,0 | 79,5 | 173,0 | 85,5 | 94 | 165,0 | 91,0 | 168,0 | 83,5 |
| 45 | 163,0 | 82,5 | 165,5 | 87,5 | 95 | 157,0 | 84,5 | 166,0 | 89,0 |
| 46 | 166,5 | 81,5 | 156,5 | 87,0 | 96 | 163,5 | 83,0 | 156,0 | 85,0 |
| 47 | 150,0 | 83,0 | 172,0 | 87,0 | 97 | 167,5 | 90,0 | 166,5 | 93,5 |
| 48 | 167,5 | 84,5 | 162,5 | 86,5 | 98 | 160,0 | 81,0 | 168,0 | 87,5 |
| 49 | 159,5 | 89,5 | 174,0 | 85,5 | 99 | 167,0 | 86,5 | 160,5 | 88,0 |
| 50 | 171,5 | 89,5 | 159,0 | 83,5 | 100 | 164,0 | 87,5 | 168,5 | 87,0 |
|
|
|
VII. ГЛОССАРИЙ
А
Аддитивная функция – функция  множеств- элементов алгебры A, для которой из условия
множеств- элементов алгебры A, для которой из условия 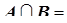 ø следует, что
ø следует, что 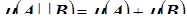 .
.
Алгебра множеств – система подмножеств A множества W, элементы которой удовлетворяют следующим требованиям:
а)  A; б) для любых A и B, принадлежащих A, следует, что
A; б) для любых A и B, принадлежащих A, следует, что  A и
A и 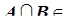 A; в) если
A; в) если 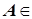 A, то
A, то  A.
A.
Б
Борелевская алгебра множеств B (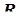 ) – система подмножеств множества действительных чисел R, получающаяся путём применения операций объединения, пересечения и дополнения к элементам системы
) – система подмножеств множества действительных чисел R, получающаяся путём применения операций объединения, пересечения и дополнения к элементам системы  , где a и b – произвольные действительные числа.
, где a и b – произвольные действительные числа.
В
Вероятностное пространство < W, A, P > - тройка объектов, где
W - множество элементарных исходов;
A -  -алгебра случайных событий;
-алгебра случайных событий;
P – вероятностная функция.
Д
Дискретная случайная величина – случайная величина, областью возможных значений которой является не более чем счётное множество D действительных чисел  . Закон распределения вероятностей дискретной случайной величины задаётся путём определения набора положительных чисел
. Закон распределения вероятностей дискретной случайной величины задаётся путём определения набора положительных чисел  , таких, что
, таких, что 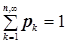 . Здесь:
. Здесь:  .
.
Дисперсия случайной величины 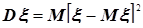 - мера разброса значений случайной величины около её математического ожидания.
- мера разброса значений случайной величины около её математического ожидания.
Доверительный интервал  - интервал, в котором с вероятностью, не меньшей чем
- интервал, в котором с вероятностью, не меньшей чем  , находится значение неизвестной числовой характеристики
, находится значение неизвестной числовой характеристики  , то есть интервал, для которого справедливо:
, то есть интервал, для которого справедливо: 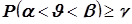 .
.
З
Закон больших чисел (ЗБЧ) – совокупность теорем, в которых на последовательность случайных величин  , налагаются условия, при которых их среднее арифметическое
, налагаются условия, при которых их среднее арифметическое  сходится по вероятности к постоянной величине – среднему арифметическому их математических ожиданий:
сходится по вероятности к постоянной величине – среднему арифметическому их математических ожиданий: 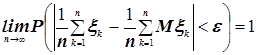 .
.
И
Измеримое пространство < W, A> - пара объектов, где W - множество элементарных исходов, A - алгебра случайных событий, на которой вводится числовая функция множеств  , которая при выполнении условий нормированности и аддитивности, называется вероятностной мерой множества A.
, которая при выполнении условий нормированности и аддитивности, называется вероятностной мерой множества A.
К
Классическое определение вероятности – определение вероятности наступления случайного события, основанное на равновозможности реализации элементарных исходов конечного множества элементарных исходов W. Если мощность множества W равна 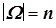 , а мощность подмножества A, являющегося случайным событием, равна
, а мощность подмножества A, являющегося случайным событием, равна  , то по классическому определению вероятности вероятность наступления случайного события A будет равна
, то по классическому определению вероятности вероятность наступления случайного события A будет равна  .
.
|
|
|
Ковариационный момент – смешанный центральный момент второго порядка  двумерной случайной величины:
двумерной случайной величины:
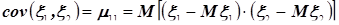 .
.
Компонента случайного вектора – скалярная случайная величина  , являющаяся проекцией случайного вектора
, являющаяся проекцией случайного вектора 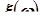 на k -тую координатную ось
на k -тую координатную ось  . То есть, если
. То есть, если  и
и  - проектор, отображающий
- проектор, отображающий 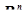 в
в  , то
, то  является композицией отображений:
является композицией отображений:
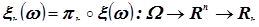 .
.
Коэффициент линейной корреляции – мера статистической силы связи между случайными величинами. Вычисляется по формуле  . Применяется в тех случаях, когда статистическая связь имеет линейный характер.
. Применяется в тех случаях, когда статистическая связь имеет линейный характер.
Критерий проверки основной гипотезы – случайная величина, статистика элементов выборки, закон распределения вероятностей которой зависит от предполагаемой гипотезы.
М
Математическое ожидание – числовая характеристика случайной величины, 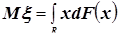 . Математическое ожидание есть среднее значение случайной величины
. Математическое ожидание есть среднее значение случайной величины  . Интерпретируется как координата центра тяжести единичной массы распределённой на числовой оси.
. Интерпретируется как координата центра тяжести единичной массы распределённой на числовой оси.
Множество элементарных исходов – множество, элементами, которого является все возможные элементарные исходы. В результате проведения испытания всегда реализуется один, и только один элементарный исход.
Н
Начальный момент k -того порядка – числовая характеристика случайной величины, являющаяся значением абсолютно сходящегося несобственного интеграла от функции 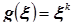 по функции распределения случайной величины, то есть:
по функции распределения случайной величины, то есть:  .
.
Независимость случайных величин. Случайные величины 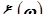 и
и  называются независимыми, если закон распределения вероятностей одной из них не зависит от другой случайной величины.
называются независимыми, если закон распределения вероятностей одной из них не зависит от другой случайной величины.
Точнее: пусть случайные величины 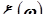 и
и  являются компонентами двумерной случайной величины
являются компонентами двумерной случайной величины  , принимающей значения в
, принимающей значения в  . Эти компоненты называются независимыми, если для любого множества B,
. Эти компоненты называются независимыми, если для любого множества B,  B(
B(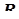 2), представимого как декартово произведение
2), представимого как декартово произведение  ,
,  и
и 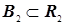 , будет справедливо:
, будет справедливо:
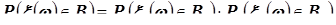 ,
,
Где 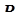 и
и  - частные вероятностные функции компонент.
- частные вероятностные функции компонент.
Независимость случайных величин непрерывного типа – Случайные величины непрерывного типа 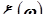 и
и  (компоненты двумерного случайного вектора) будут независимыми тогда, только тогда, когда для любой пары
(компоненты двумерного случайного вектора) будут независимыми тогда, только тогда, когда для любой пары  выполняется равенство
выполняется равенство 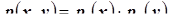 , где
, где 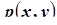 - плотность вероятности двумерного случайного вектора
- плотность вероятности двумерного случайного вектора  , а
, а 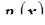 и
и  - плотности вероятностей его компонент
- плотности вероятностей его компонент 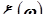 и
и  .
.
|
|
|
Независимость случайных величин дискретного типа – Случайные величины дискретного типа 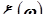 и
и  (компоненты двумерного случайного вектора) будут независимыми тогда, только тогда, когда для любой пары
(компоненты двумерного случайного вектора) будут независимыми тогда, только тогда, когда для любой пары 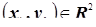 выполняется равенство
выполняется равенство  , где
, где  , а
, а  и
и  .
.
Независимость случайных событий. Случайные события называются независимыми, если условная вероятность наступления любого из них равна его безусловной вероятности: 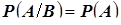 или
или 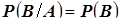 .
.
Непрерывная случайная величина – случайная величина, областью возможных значений которой является множество D мощности континуум и положительной меры Лебега. Закон распределения вероятностей непрерывной случайной величины задаётся путём определения на этом множестве плотности вероятности  - кусочно-непрерывной, неотрицательной функции, такой что
- кусочно-непрерывной, неотрицательной функции, такой что  .
.
Несмещённость точечной оценки. Точечная оценка 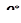 числовой характеристики
числовой характеристики  называется несмещённой, если
называется несмещённой, если  .
.
О
Остаточная дисперсия – мера разброса значений одной из компонент (например 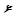 ) двумерной случайной величины
) двумерной случайной величины  около её математического ожидания, вызванного внутренними свойствами этой компоненты. При линейном виде статистической связи между компонентами величина остаточной дисперсии компоненты
около её математического ожидания, вызванного внутренними свойствами этой компоненты. При линейном виде статистической связи между компонентами величина остаточной дисперсии компоненты 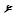 равна
равна 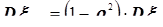 , где
, где  - коэффициент линейной корреляции между компонентами
- коэффициент линейной корреляции между компонентами  и
и 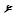 .
.
Ошибка I рода – отклонение верной гипотезы  . Возникает в том случае, когда при справедливости в реальности гипотезы
. Возникает в том случае, когда при справедливости в реальности гипотезы  наблюдаемое значение критерия
наблюдаемое значение критерия 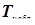 попадает в критическую область
попадает в критическую область 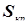 . Вероятность ошибки I рода равна
. Вероятность ошибки I рода равна  .
.
Ошибка II рода – принятие неверной гипотезы  . Возникает в том случае, когда при справедливости в реальности гипотезы
. Возникает в том случае, когда при справедливости в реальности гипотезы 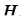 наблюдаемое значение критерия
наблюдаемое значение критерия 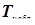 попадает в область допустимых значений
попадает в область допустимых значений  . Вероятность ошибки II рода равна
. Вероятность ошибки II рода равна  .
.
П
Повторные независимые испытания – серия одинаковых испытаний, в каждом из которых с постоянными вероятностями p и q может произойти только одно из взаимно противоположных событий A или  .
.
Плотность вероятности – неотрицательная, кусочно-непрерывная функция, удовлетворяющая условию: 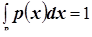 . Плотность вероятности описывает распределение вероятностей случайной величины
. Плотность вероятности описывает распределение вероятностей случайной величины 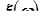 непрерывного типа.
непрерывного типа.
Р
Распределение 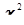 - (распределение Пирсона) распределение вероятностей случайной величины
- (распределение Пирсона) распределение вероятностей случайной величины 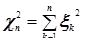 , где все
, где все  независимые случайные величины, имеющие нормальное распределение вероятностей N(0;1).
независимые случайные величины, имеющие нормальное распределение вероятностей N(0;1).
Распределение Стьюдента – (t -распределение) распределение вероятностей случайной величины  , где все
, где все 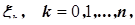 независимые случайные величины, имеющие нормальное распределение вероятностей N(0;1).
независимые случайные величины, имеющие нормальное распределение вероятностей N(0;1).
Распределение Фишера-Снедекора – (F -распределение) распределение вероятностей случайной величины 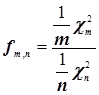 .
.
Ряд распределения – таблица, состоящая из двух строк, с помощью которой задаётся закон распределения дискретной случайной величины:
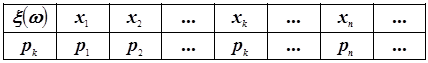 .
.
Где  или
или 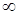 ;
;  . Всегда
. Всегда 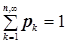 .
.
С
Свёртка функций распределения – несобственный интеграл, определяющий функцию распределения случайной величины, являющейся суммой независимых случайных величин. Если  , то функция распределения
, то функция распределения  будет равна:
будет равна: 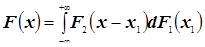 , где
, где  и
и  - функции распределения случайных величин-слагаемых.
- функции распределения случайных величин-слагаемых.
Состоятельность точечной оценки. Точечная оценка 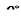 числовой характеристики
числовой характеристики  называется состоятельной, если она сходится по вероятности к этой точечной оценке, то есть:
называется состоятельной, если она сходится по вероятности к этой точечной оценке, то есть: 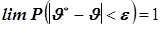 .
.
Статистика – любая функция элементов выборки  :
:  .
.
Сходимость по вероятности. Последовательность случайных величин 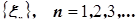 сходится по вероятности к случайной величине
сходится по вероятности к случайной величине  (обозначение:
(обозначение: 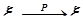 ), если выполняется условие
), если выполняется условие  .
.
Сходимость по распределению. Последовательность случайных величин 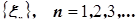 сходится по распределению к случайной величине
сходится по распределению к случайной величине  (обозначение:
(обозначение: 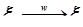 ), если соответствующая последовательность функций распределения
), если соответствующая последовательность функций распределения  слабо сходится к функции распределения
слабо сходится к функции распределения 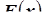 случайной величины
случайной величины  (
(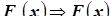 ).
).
У
Условная вероятность  - вероятность наступления случайного события A, вычисленная при предположении, что случайное событие B произошло. Определяется по формуле:
- вероятность наступления случайного события A, вычисленная при предположении, что случайное событие B произошло. Определяется по формуле:  .
.
Условная плотность вероятности  - плотность вероятности условной случайной величины
- плотность вероятности условной случайной величины 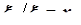 , является законом распределения вероятностей второй компоненты при любом фиксированном значении первой компоненты. Определяется по формуле:
, является законом распределения вероятностей второй компоненты при любом фиксированном значении первой компоненты. Определяется по формуле:  , где
, где  - плотность вероятности двумерной случайной величины
- плотность вероятности двумерной случайной величины  ,
,  - частная плотность вероятности первой компоненты
- частная плотность вероятности первой компоненты  .
.
Ф
Функция распределения – функция 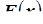 , описывающая изменение вероятности случайного события
, описывающая изменение вероятности случайного события 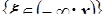 при изменении x, то есть
при изменении x, то есть 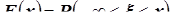 . Определяя функцию распределения
. Определяя функцию распределения  , мы задаём закон распределения вероятностей случайной величины
, мы задаём закон распределения вероятностей случайной величины  .
.
Функция распределения вектора - функция  , описывающая изменение вероятности случайного события
, описывающая изменение вероятности случайного события  , где
, где  , при изменении
, при изменении  , то есть
, то есть  . Определяя функцию распределения
. Определяя функцию распределения  , мы задаём закон распределения вероятностей случайного вектора
, мы задаём закон распределения вероятностей случайного вектора  .
.
Функция регрессии – функция, описывающая зависимость значений условных математических ожиданий одной из компонент двумерной случайной величины от другой компоненты. Функция 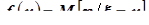 - функция регрессии компоненты
- функция регрессии компоненты  на изменение компоненты
на изменение компоненты  . Функция
. Функция  - функция регрессии компоненты
- функция регрессии компоненты  на изменение компоненты
на изменение компоненты  .
.
Х
Характеристическая функция – комплексно-значная функция действительного аргумента, являющаяся математическим ожиданием функции  случайной величины
случайной величины  , где
, где  , то есть:
, то есть: 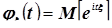 .
.
Ч
Частная функция распределения – функция распределения любой k -той компоненты  вектора
вектора  . Определение частной функции распределения основано на свойстве согласованности функции распределения многомерной случайной величины, например, если n =2, то
. Определение частной функции распределения основано на свойстве согласованности функции распределения многомерной случайной величины, например, если n =2, то  и
и 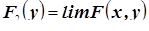 .
.
Частные распределения компонент случайного вектора - распределения вероятностей компонент вектора, являющихся скалярными случайными величинами. Частное распределение каждой компоненты получается как проекция вероятностной функции вектора на соответствующую координатную ось. Если 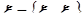 и P вероятностная функция вектора, то частное распределение
и P вероятностная функция вектора, то частное распределение  компоненты
компоненты 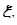 определяется равенством:
определяется равенством: 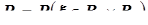 , где
, где  B (
B ( ). Аналогично, частное распределение
). Аналогично, частное распределение  компоненты
компоненты  определяется равенством:
определяется равенством: 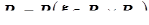 , где
, где 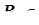 B (
B ( ).
).
Ц
Центральная предельная теорема (ЦПТ) – совокупность теорем, в которых на последовательность случайных величин 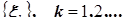 , налагаются условия, при которых их центрированная и нормированная сумма
, налагаются условия, при которых их центрированная и нормированная сумма 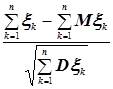 сходится по рас
сходится по рас
|
|
|


