Модуль 3. Случайные величины и векторы

Цель модуля: На основе понятия функции, как правиле отображения одного множества в другое, ознакомиться с понятием случайной величины. Понять универсальность использования случайной величины в решении различных практических задач. Изучить типы случайных величин и наиболее часто встречающиеся на практике законы распределения вероятностей.

Решая конкретную задачу по теории вероятностей, мы, прежде всего, определяем чёткое название элементарного исхода. Все возможные элементарные исходы объединяются во множество элементарных исходов W. Формулируя названия различных подмножеств множества элементарных исходов, определяем алгебру случайных событий A. На измеримом пространстве < W, A, > Разумным способом определяем вероятностную функцию P. То есть, при решении задачи строится вероятностное пространство < W, A, P >. Значения вероятностной функции на каждом случайном событии мы трактуем как вероятность наступления этого случайного события.

Элементарными исходами, образующими множество W, могут быть объекты любой природы: наборы шаров различных цветов, наборы деталей различного качества, наборы карт различных номиналов, полученные каким-либо способом, определяемым условием испытания; последовательности событий A и , наступающих при проведении одинаковых испытаний по какому-либо правилу. Введение понятия случайной величины позволяет каждому элементарному исходу, независимо от его природы/ поставить в соответствие некоторый элемент (точку) из пространства .

Случайная величина  – это измеримое отображение множества элементарных исходов W в пространство , то есть . Измеримость отображения означает, что для любого борелевского множества B,  B(), вероятность случайного события  равна вероятности случайного события A, где событие A, являющееся элементом алгебры А A, есть полный прообраз множества В. То есть, , где .

В соответствии с типом вероятностной функции P, описывающей распределение вероятностей значений случайной величины , рассматриваются два типа случайных величин: дискретный и непрерывный.

Для любого испытания, определяющего элементарные исходы как объекты некоторой природы (наборы карт, выборки шаров, извлеченные детали и т.п.), мы можем теперь, с помощью понятия случайной величины, случайные события трактовать как числовые, борелевские множества в пространстве .

Переход к трактовке случайных событий, независимо от содержания условия задачи, как числовых множеств точек в , являющихся борелевскими множествами, позволяет ввести определение функции распределения случайной величины.

Для любой точки  пространства  множество, точек принадлежащих интервалу , обозначим  Ясно, что - борелевское множество. Случайное событие  можно трактовать так: случайная величина  принимает числовые значения меньшие, чем x, т.е.: 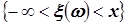. Для каждого x мы можем определить вероятность события 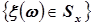, то есть число . Если x будет переменной величиной, то эта вероятность будет функцией от этого x. Эту функцию, обозначим её , будем называть функцией распределения случайной величины : .

Если  - дискретного типа, то её функция распределения имеет вид: . Если  - непрерывного типа, то её функция распределения имеет вид: .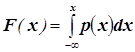

Независимо от типа случайной величины вероятность любого случайного события B, то есть , будет равна приращению значения функции распределения на множестве B: .

По любой вероятностной функции P можно построить функцию распределения . Справедливо и обратное утверждение: всякая функция, обладающая тремя рассмотренными свойствами, является функцией распределения  и по ней можно единственным образом построить вероятностную функцию P.

Рассматривая композицию отображений , приходим к понятию k -той компоненты векторной случайной величины: , где  и к представлению  Частная вероятностная функция  и частная функция распределения 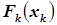 каждой той компоненты  определяется по вероятностной функции P и функции распределения  векторной случайной величины .

Понятие независимости случайных величин – одно из важнейших понятий теории вероятностей. Оно вводится как понятие независимости компонент векторной случайной величины .

Компоненты 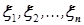 называются независимыми, если для любого множества , принадлежащего , вероятность  равна произведению вероятностей , , где  - проекция множества  на . Рассматриваются три формы критерия независимости случайных величин. Показывается, что по распределению вероятностей вектора всегда можно найти распределения вероятностей его компонент, а по распределениям вероятностей компонент не всегда можно построить распределение вероятностей исходного вектора.