 |
Аксиоматика А.Н. Колмогорова.
|
|
|
|
Цель модуля: Узнать принцип построения общей вероятностной модели на основе аксиом А.Н. Колмогорова. Ознакомиться с правилами построения алгебры борелевских множеств и типами вероятностных функций, задаваемых на измеримых пространствах.
Вероятностная функция P любому случайному событию A, являющемуся элементом алгебры A, ставит в соответствие число  ,
,  . Кратко это записывается так: P: A
. Кратко это записывается так: P: A 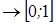 . Это число
. Это число  называется «вероятностью наступления случайного события A» и оно понимается как значение меры возможности наступления, осуществления события A при однократном проведении испытания, опыта. Чем больше это число
называется «вероятностью наступления случайного события A» и оно понимается как значение меры возможности наступления, осуществления события A при однократном проведении испытания, опыта. Чем больше это число  , тем больше у испытателя уверенность в возможности наступления, осуществления события A при проведении испытания и, наоборот, чем меньше это число
, тем больше у испытателя уверенность в возможности наступления, осуществления события A при проведении испытания и, наоборот, чем меньше это число  , тем меньше у него уверенность в возможности его наступления, осуществления.
, тем меньше у него уверенность в возможности его наступления, осуществления.
Но ранее функция P вводилась посредством предварительного, аксиоматического установления соответствия  . Это соответствие всегда можно было установить, так как в рассматриваемых моделях элементарные исходы представлялись в виде конечной или бесконечной последовательности
. Это соответствие всегда можно было установить, так как в рассматриваемых моделях элементарные исходы представлялись в виде конечной или бесконечной последовательности  или
или  . То есть, мы могли вводить функцию P, если множество W было конечным или счётным и мы могли мысленно представить себе каждый элементарный исход.
. То есть, мы могли вводить функцию P, если множество W было конечным или счётным и мы могли мысленно представить себе каждый элементарный исход.
Но есть большое количество примеров описания испытаний, в которых элементарные исходы нельзя представить в виде конечной или бесконечной последовательности. Например, выбор наудачу точки из отрезка  ; определение времени горения электрической лампы; измерение высоты растения пшеницы; взвешивание зерен одного колоса пшеницы.
; определение времени горения электрической лампы; измерение высоты растения пшеницы; взвешивание зерен одного колоса пшеницы.
Такие множества, все элементы которых нельзя представить в виде конечной или бесконечной последовательности, называются множествами мощности континуум.
|
|
|
Сохранив основные понятия и определения, сделанные при рассмотрении примеров, определяющих множества конечной или счетной мощности, и расширив определение алгебры на случай рассмотрения счетных последовательностей событий до определения s -алгебры, мы, следуя А.Н. Колмогорову, вероятностную функцию P определяем как числовую функцию определенную на элементах s -алгебры A. Но, если раньше нормированность и аддитивность вероятностной функции P вытекали автоматически из ее определения по набору положительных чисел  то теперь, при построении общей вероятностной модели, нормированность и s -аддитивность функции P требуется аксиоматически. То есть, всякая функция, определенная на s -алгебре случайных событий, принимающая числовые значения и обладающая свойствами нормированности и s -аддитивности, является вероятностной функцией.
то теперь, при построении общей вероятностной модели, нормированность и s -аддитивность функции P требуется аксиоматически. То есть, всякая функция, определенная на s -алгебре случайных событий, принимающая числовые значения и обладающая свойствами нормированности и s -аддитивности, является вероятностной функцией.
Рассматривая свойства вероятностной функции, приходим к выводу, что вместо s -аддитивности аксиоматически можно требовать или «непрерывность сверху», или «непрерывность снизу», или «непрерывность в нуле». (Аналогично тому, как при изучении геометрии, основывающуюся на аксиомах Евклида, вместо пятой аксиомы параллельности можно принять аксиому о том, что сумма углов треугольника равна p.)
Тройку объектов < W, A, P > называется вероятностным пространством. Для того чтобы показать как практически реализуется процесс построения вероятностного пространства по Колмогорову, рассматриваются такие испытания, элементарными исходами которых будут действительные числа (или – точки вещественной оси).
Однако, если мы будем в качестве алгебры событий, то есть в качестве области определения вероятностной функции P брать s -алгебру всех подмножеств множества действительных чисел, то получится очень необозримая алгебра множеств, на которой будет невозможно задать числовую функцию. Поэтому в качестве алгебры случайных событий предлагается взять алгебру борелевских множеств. Так как мы знаем как строится, конструируется из простейших множеств – полуинтервалов любое борелевское множество, то тогда, исходя из определения функции P на полуинтервалах, можно будет определить вероятностную функцию на всей s -алгебре борелевских множеств действительных чисел.
|
|
|
Приступая к практическому рассмотрению возможных типов и конкретных примеров вероятностных функций, в качестве множества элементарных исходов W рассматриваются множества двух типов.
I тип. W - множества вещественных чисел, имеющие не более чем счетную мощность и лебегову меру равную нулю, то есть ç W ç = n или a и  (W)=0.
(W)=0.
II тип. W - множества вещественных чисел, имеющие мощность континуум и положительную лебегову меру, то есть ç W ç = c и 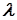 (W)>0.
(W)>0.
Соответственно этим двум типам множеств элементарных исходов определяются два типа вероятностных функций.
Функция P называется вероятностной функцией дискретного типа, если область её определения есть множество первого типа, а множеством ее возможных значений является не более чем счетное множество положительных чисел  таких что
таких что  .
.
Функция P называется вероятностной функцией непрерывного типа, если областью еёопределения является множество второго типа. Задаётся такая функция с помощью определения кусочно-непрерывной неотрицательной функции  , называемой плотностью вероятностей, такой что
, называемой плотностью вероятностей, такой что 
Вероятность любого случайного события A, являющегося элементом алгебры B( ), в зависимости от типа функции P определяется так:
), в зависимости от типа функции P определяется так:
 или
или  .
.
|
|
|


