 |
В деятельностной технологии обучения
|
|
|
|
Серьезными недостатками существующей системы контроля в обучении являются: 1) нерегулярность (эпизодичность), 2) неполный охват проверкой всего содержания обучения (выборочность проверки), 3) отсутствие проверки самого процесса работы студента (проверяется в основном конечный результат), 4)недостаточная в вовлеченность самих обучающихся в самоконтроль (слабость внутренней обратной связи) (М.Н. Скаткин, 78). В традиционной педагогике контроль учебно-воспитательного процесса воспринимается как дополнительная функция, сопровождающая основной процесс приобретения знаний и умений и воспитывающего воздействия на учащихся. В деятельностной технологии обучения контроль и самоконтроль познавательной деятельности органически входит в процесс учения.
Самопроектирование деятельности учеником, прогнозирование ее отдельных стадий требуют постоянного контроля за ходом своей деятельности учения со стороны обучающегося. Студент проводит обоснование и проверку правильности выполняемых или планируемых действий и операций, высказываемых гипотез. Оценка обоснованности и правильности своих действий является обязательной составляющей всякой деятельности, в том числе и деятельности учебной, хотя в силу различных причин проверка правильности решения задач по физике в обучении практически не осуществляется, что превратилось в актуальную методическую проблему, включающую а) воспитание культуры, потребности обосновывать и контролировать предпринимаемые действия, действовать на основе знания, а не только интуиции, б) формирование системы контроля правильности выполнения предметной деятельности в физике, в) включить в программу обучения конкретный материал, необходимый для осуществления различных видов проверок.
|
|
|
Проверку правильности промежуточных действий и полученного результата осуществляют в следующей последовательности: проверка правильности выполнения математических действий, проверка размерности расчетной формулы, оценка реальности численного значения физической величины, удовлетворение принципу соответствия в предельных переходах. Самыми сильными методами проверки являются решение задачи еще одним способом и экспериментальная проверка результата.
Приемы проверки на уровне методов, действий и операций должны быть представлены в учебной программе соответствующим содержанием, которое легко выявить, планируя те или иные способы проверки. Например, общее ускорение тел системы, соединенных нерастяжимыми нитями, определяют через решение системы уравнений динамики каждого тела и непосредственно через отношение суммы внешних сил к общей массе тел системы. Напряженность электростатического поля в однородном диэлектрике находят с помощью теоремы Гаусса для электрического смещения и для напряженности поля с предварительным нахождением связанного электрического заряда, приращение импульса вычисляют как через приращение скорости материальной точки, так и через импульс действующей силы и т.д. Проверка на уровне отдельных операций: силовое взаимодействие тел контролируется парным характером сил, правильность построения изображения в тонкой линзе использованием третьего «замечательного» луча и др.
Контроль индивидуальной учебной деятельности студентов со стороны преподавателя при коллективной форме обучения проводится в форме контролируемой самостоятельной работы (КСР) студентов при выполнении специальных заданий, разработанных на единой структурной основе или по единому сюжету. Приводим для примера такое задание по теме «Распределение Ферми-Дирака»:
|
|
|
Уровень Ферми меди (серебра, цинка …) при 0 К равен 7,0 (5,48; 9,39…)эВ. Найдите температуру вырождения электронного газа в металле. Чему равна концентрация свободных электронов? Проверьте полученный результат другим способом. Найти при 0 К максимальную плотность квантовых состояний, наибольший и средний импульс свободных электронов, долю электронов, импульсы которых не превышают его среднего значения. Вывести закон распределения свободных электронов по импульсам при 0 К и температуре Т».
Помимо того, что в вариантах этого задания меняется род металла, частично изменяются в них и условия. Например, требуется найти среднюю энергию, среднюю скорость и т.д. Такое задание позволяет легко контролировать выполнение отдельных ее этапов во время аудиторного занятия.
Главное назначение контроля и самоконтроля в учебном процессе по физике – это формирование, закрепление и упрочнение знаний. Комплексно это показано на конкретном примере задач из домашнего задания по разделу электромагнетизма для студентов МГТУ им. Н.Э.Баумана.
Задача 1. Сферический конденсатор с внутренним радиусом R1=1см и внешним радиусом R0=3R1 имеет внутри два концентрических сферических плотно прилегающих друг к другу и к обкладкам конденсатора диэлектрического слоя с границей раздела радиуса R2=2R1. Внутренний диэлектрик имеет постоянную диэлектрическую проницаемость e1=1,5.Диэлектрическая проницаемость второго слоя зависит от расстояния r от центра сфер: e2=(R02+R12)/(R21+r2). Конденсатору сообщён заряд q=0,1p нКл. Найти зависимости от расстояния r: а) электрического смещения, напряженности и объёмной плотности энергии электрического поля в конденсаторе, б) поляризованности диэлектриков и объёмной плотности связанного заряда. Найти поверхностную плотность связанного заряда на внутренних и внешних поверхностях слоёв диэлектриков. Найти электроёмкость и энергию конденсатора. Построить графики электрического смещения D, напряжённости E, поляризованности Р, объёмной плотности связанного заряда r¢. Выполнить проверку полученных результатов, а также сравнить значения электроёмкости с расчетом по формуле электроёмкости сферического конденсатора. Сделайте выводы.
|
|
|
Решение. Уясним содержание и требование задачи. Перепишем e2(r) в виде e2=10R12/(R12+r2), изобразим на рисунке зависимость диэлектрической проницаемости диэлектриков в конденсаторе от r.
Расчет характеристик электростатического поля начнём с определения электрического смещения D(r), функция которого от r не зависит от наличия диэлектриков. В данной сферически-симметричной задаче можно применить теорему Гаусса для электрического смещения: 
, где Sr – поверхность сферы произвольного радиуса r.
Учитывая в данной задаче независимость физических величин от углов сферических координат, получаем: D=Dr=q/4pr2. На поверхностях радиусами R1 и R2 имеем, cсоответственно, D=(1/4) мкКл/м2 и D0 =(1/36) мкКл/м2. Используя связь напряжённости и электрического смещения для изотропных диэлектриков E=D/e0e, найдем: E1=q/4pe0e1r2 и E2=q(R12+r2)/4pe0×10R12×r2. Правильность полученных результатов подтвердим, используя условие разрыва нормальных составляющих напряжённости электрических полей на границe двух диэлектриков e1E1(R2)=e2E2(R2) при r=R2, или 1,5E1(R2)=2E2(R2), где E1(R2)=q/4pe0×6R12 и E2(R2)=q/4pe0×8R12. Проверка подтверждает правильность полученных выражений для напряжённостей поля. (При необходимости построить графики функций E1(r) и E2(r) исследуем последние на экстремум в области R1 – R0).
Используя связь поляризованности изотропного диэлектрика с напряжённостью электрического поля в точке, находим: P1=0.5e0E1=q/4p×3r2 (для внутреннего слоя диэлектрика) и P2=q(9R12-r2)/4p×10×R21×3r2 (для внешнего). Правильность полученных выражений подтвердим, используя формулу определения вектора электрического смещения 
. В проекции на радиальное направление имеем: D=e0Е+P. Для внутреннего диэлектрика имеем: q/4pr2=q/4pe1r2+q/4p×3r2, или после упрощения тождества и подстановки в выражение значения e1, имеем 1=2/3+1/3. Для второго диэлектрика получаем:
После преобразования получаем тождество. Проверка подтвердила правильность результата. Поляризованность P(R0)=0, т.к. значение диэлектрической проницаемости в этой точке равно 1, как для вакуума.
|
|
|
Поверхностная плотность связанного заряда s' равна проекции поляризованности на внешнюю нормаль к рассматриваемой поверхности. Для внешней поверхности слоев диэлектриков внешняя нормаль совпадает по направлению с радиусом 
, для внутренней поверхности, обращенной к оси симметрии, она имеет направление, противоположное радиальному. При R1 находим s1'(R1)=P1cosp=-q/4p×3R2= - (1|12) мкКл/м. При R2 на внешней поверхности первого слоя s'1(R2)= P2cos0 =(1/48) мкКл/м2, а на внутренней поверхности второго диэлектрика s2(R2)= - q(9R12-R22)/4pR22×10R12= - (1/8) мкКл/м2. На внешней границе второго диэлектрика s2'(R0)=0.
Объёмная плотность связанного заряда r'=-div 
. В сферических координатах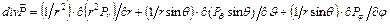 
В случае независимости поляризованности от угловых координат, получаем
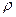¢=-(r2 P)¢/r2, где штрихом обозначена производная по координате r. Получаем r'1= 0, т.е. внутри сферического диэлектрика с постоянной диэлектрической проницаемостью не возникает объёмного связанного заряда. Для r¢2 находим r'2=q/4pr×5R12.
Для оценки правильности проведённых расчётов проверим справедливость теоремы Гаусса для напряжённости электрического поля в диэлектрике, в выражение которой войдёт связанный заряд: 
, или 
, где q¢2(R2) -связанный заряд на внутренней поверхности второго слоя диэлектрика. Интеграл выражает связанный заряд, распределённый по объёму второго диэлектрика в пределах произвольно выделенной сферы радиуса r. Сумма связанных зарядов на внутренней и внешней поверхностях первого диэлектрика равна нулю и в написанное выражение не входит. После подстановки соответствующих формул, получаем выражение: 
, являющееся тождеством.
Для нахождения электроёмкости конденсатора, вычислим напряжение на его обкладках 
, используя формулу связи разности потенциалов с напряжённостью электростатического поля. Получим U=7q/4pe0R1×60 + q/4pe0R1×3 = 9q/80pe0R1. Тогда С =q/U= 80pe0R1/9=2,5 пФ. Расчёт электроёмкости по известной формуле сферического конденсатора C=4pe0eR1R2/(R2-R1) даёт другой результат С=0,83пФ (при e=1,5). Это расхождение объясняется неприменимостью для данного случая стандартной формулы электроёмкости сферического конденсатора, которая относится к однородному изотропному диэлектрику с постоянной диэлектрической проницаемостью, заполняющему сферический конденсатор.
Объёмная плотность энергии определяется квадратом модуля напряжённости поля в рассматриваемой точке, т.е. w=e0eE2/2. Получаем во внутреннем диэлектрике w1=q2/32p2e0e1r4 и проверяем по формуле w=D2/2e0e1, подставив в него выражения для электрического смещения. Аналогично находим и проверяем зависимость w2=q2(R12+r2)/32p2e0r4 ×10R12 для внешнего диэлектрика.
Энергию заряженного конденсатора вычислим двумя способами. В первом способе рассчитаем энергию электростатического поля в конденсаторе, используя выражения для её объёмной плотности.
|
|
|
Второй способ - использование формул энергии заряженного конденсатора W=q2/2С и W= СU2/2. Обе формулы дают одинаковый результат.
Задача 2 Коаксиальный кабель состоит из полой длиной прямой круглой толстостенной цилиндрической трубки, внутренний и внешний радиусы которой соответственно равны R=1см и R0=2R, и наружной проводящей цилиндрической поверхности (тонкостенная трубка) радиусом 3R. Постоянный электрический ток I=10 А течет по внутренней трубке и возвращается по наружной цилиндрической поверхности. Магнитная проницаемость неферромагнитного материала толстостенной трубки меняется с расстоянием r от оси трубки по закону m=(2R02-r2)/R2. Магнитную проницаемость окружающей среды принять за единицу. Найти зависимости от r напряжённости и индукции магнитного поля, намагниченности и плотности токов намагничивания, изобразить их графически. Найти молекулярный ток намагничивания на внутренней и внешней поверхностях трубки. Найти магнитную индукцию внутри трубки, используя теорему о циркуляции магнитной индукции в магнетике. Получить зависимость объемной плотности энергии магнитного поля от расстояния. Найти магнитный поток внутри кабеля, а также магнитную энергию и индуктивность единицы длины кабеля. Выполните проверку всех полученных результатов.
Решение. Уясним содержание и требование задачи. Перепишем выражение для магнитной проницаемости материала трубки в виде m=(8R2-r2)/R2. Она убывает от значений 7 до 4 при перемещении к периферии трубки (изобразите на графике). По причине цилиндрической симметрии векторные линии магнитного поля, создаваемого электрическим током в трубке, представляют собой концентрические окружности с центрами на оси трубки, лежащие в плоскостях, перпендикулярных этой оси. Напряженность поля вычисляем по теореме о циркуляции вдоль контура l, совпадающего с векторной линией – окружностью радиуса r. Запишем 
При r<R имеем H1=0 (поле отсутствует), т.к. I=0 в этой области. Внутри трубки R<r<R0 получаем: 
Окончательно находим H2=I(r2-R2)/6pR2r. В области вне трубки 2R<r<3R находим, что магнитное поле совпадает с полем длинного прямого проводника H3=I/2πr. Магнитное поле вне кабеля также отсутствует Н4=0,т.к. при r>R сумма токов в правой части теоремы о циркуляции напряженности поля равна нулю. Внешняя проводящая оболочка экранирует магнитное поле от распространения за пределы кабеля.
По формуле В=m0mН находим соответствующие выражения для магнитной индукции: 
и В4=0.
Проверим полученные результаты, рассмотрев поведение этих величин на внутренней и внешней поверхностях трубки. Тангенциальные составляющие напряженности магнитного поля не терпят разрыва 
а магнитной индукции на границе области 2-3 при 
терпят разрыв 
. Имеем тождества 
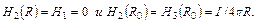Также подтверждается соотношение 
для тангенциальных составляющих магнитной индукции.
Намагниченность материала трубки 
Исследование этой функции показало, что ее график имеет максимум внутри трубки при r=1,83R. Проверка правильности расчета намагниченности осуществляется формулой связи магнитной индукции, напряженности магнитного поля и намагниченности магнетика 
Плотность тока намагничивания в цилиндрических координатах:
где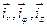 
- единичные орты цилиндрической системы координат. Учитывая осевую
симметрию, получаем 
.
Плотность молекулярных токов намагничивания уменьшается от максимального значения 0,64 кА/м2 на внутренней поверхности трубки до нуля на её внешней поверхности. Силу тока намагничивания в трубке I¢ вычислим двумя способами, используя связь с намагниченностью 
и с плотностью тока намагничивания 
, которые дают одинаковые результаты. На внутренней поверхности трубки (r=R) поверхностная плотность молекулярного тока намагничивания равна нулю, а на внешней (r=2R) она равна i¢=I¢/2pR0=3I/4pR=0,24 кA/м.
Для нахождения индукции магнитного поля внутри трубки вторым способом запишем выражение теоремы о циркуляции магнитной индукции в магнетике вдоль векторной линии магнитного поля радиусом R<r<R0, т.е. 
- сила тока, текущего через поперечное сечение трубки, ограниченное радиусом r. После выполнения вычислений получаем найденное ранее выражение для В2.
Объемную плотность энергии в каждой из областей вычисляем по формулам: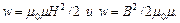 
Имеем совпадающие результаты:
Объемная плотность магнитного поля на внешней границе трубки с внутренней стороны достигает 16 мДж/м3, а с внешней стороны – 4 мДж/ м3, т.е. в 4 раза меньше. Это полностью согласуется с тем, что в формулах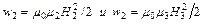 
(при равенстве напряженностей магнитного поля на границе) магнитная проницаемость
. Большая плотность энергии магнитного поля внутри трубки связана с большими затратами на намагничивание материала трубки.
Вычислим энергию магнитного поля, приходящуюся на единицу длины кабеля (h=1 м), используя объемную плотность энергии,
.
Окончательно находим W=m0I2h(0,78+ln1,5)/4p=12 мкДж, где первое слагаемое соответствует магнитной энергии внутри толстостенной трубки, второе слагаемое - энергии магнитного поля в пространстве между внутренним и внешним проводниками кабеля. Зная энергию единицы длины кабеля с током, можно найти индуктивность единицы длины этого кабеля из формулы W=LI2/2. Получаем: L=m0h(0,78+ln1,5)/2p=0,24 мкГн
Магнитный поток через продольное сечение кабеля единичной длины находим вычислением интегралов
Первое слагаемое соответствует магнитному потоку, создаваемому во внутреннем проводнике кабеля, а второе – в пространстве между внутренней и внешней оболочками кабеля. Если вычислить индуктивность единичной длины кабеля через магнитный поток L=Ф/I, то получим L=m0h(1,4+ln1,5)/2p=0,36 мк Гн завышенный неверный результат. Расхождение этих двух выражений для индуктивности связано со слагаемым, относящимся к магнитному полю внутри толстостенной трубки из магнитного материала. Второй способ расчета индуктивности системы не учитывает потерю энергии, связанную с намагничиванием материала внутренней трубки кабеля.
* * *
Видим, что решение задачи в деятельностной технологии обучения, сопровождающееся самоконтролем со стороны студента, знаменует глубокий учебно-познавательный процесс обучения физике.
|
|
|
