 |
13. Использование теории полезности в актуарных расчетах. Выбор наиболее выгодного договора с помощью функции полезности
|
|
|
|
13. Использование теории полезности в актуарных расчетах. Выбор наиболее выгодного договора с помощью функции полезности
Страховая премия устанавливается страховой компанией, исходя из готовности страхователей платить за страховую защиту. Здесь вступает в силу принцип эквивалентности.
Принцип основывается на теории полезности и может быть объяснен следующим образом: приобретая страховой полис, индивид снижает уровень своего благосостояния на цену страхования – негативный момент. С другой стороны, наступления страхового случая также ведет к снижению благосостояния, обычно гораздо более ощутимому. Основным моментом является то, какая потеря более весома: потеря суммы, равной страховой премии, или суммы ущерба при страховом случае.
Математически эта ситуация иллюстрируется следующим образом:
Определим функцию полезности индивида как U(w), где w – уровень благосостояния в руб. U(w) определяется экспертным путем.
Предположим, что индивид не склонен к риску.
Свойства функции:
- возрастающая (вид функции) функция, т. е. U’(x)> 0
- скорость возрастания убывает, т. е. U”(x)< 0
Примеры: ln(x); xa (0< a< 1); 1-e-x; их линейные комбинации.
Использование функции полезности осуществляется следующим образом:
обозначим: w – начальный капитал страхователя (благосостояние); БП – плата за страховой полис; х – ущерб в течение срока действия договора (с. в. с законом распределения ущерба с плотностью f(x))
Тогда принцип эквивалентности U(w-БП)=М(U(w-x))
Страхователю выгодно страхование, когда U> M.
Вычислив функцию для различных вариантов договоров и отказа от страхования вообще, можно выяснить, что наиболее выгодно страхователю с т. зрения полезности.
|
|
|
Umax=U(w-0)=U(w) – убытков не будет
Umin=U(w-xmax)=U(w-b) – убытки максимальны.
Все значения функции полезности находятся в этих пределах Umin< =U(x)< =Umax
Отказ от страхования соответствует функции полезности M(U(w-x)).
Значение функции полезности для различных договоров определяется согласно условию договоров: брутто-премии и доли ответственности за риск.
Максимальное значение функции полезности – это наиболее выгодный договор для страхователя, минимальное – наиболее выгодный для страхователя договор.
содержание
14. Степень риска и ее роль в актуарных расчетах
В качестве первичной оценки целесообразности принятия нового риска в страховании принято использовать « степень риска ». Статистический смысл этого показателя – коэффициент вариации. Он рассчитывается как отношение среднего квадратического отклонения величины суммарного ущерба в портфеле к математическому ожиданию этого ущерба. (СКО/МО) Если портфель однороден, то из свойства одинаково распределенных случайных величин следует, что при увеличении портфеля в n раз, коэффициент вариации уменьшится к (корень из n) раз. Поэтому достаточно рассмотреть ситуацию для одного договора.
Пусть p – вероятность наступления страхового случая, и тогда величина ущерба Х распределена по известному закону. Это позволяет рассчитать условное математическое ожидание М(Х|А)и дисперсию D(Х|А), затем на их основе рассчитываются полные соответствующие характеристики М(Х) и D(Х)
Это позволяет оценить степень риска как
Нормальное значение K< 0, 3.
Видно, что когда величина ущерба при наступлении страхового случая фиксирована, т. е. 
, то под знаком корня остается только второе слагаемое и возникает формула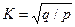 
, она показывает опасность принятия отдельных рисков с очень малой вероятностью р, особенно, если при этом велика страховая сумма. При фиксированном ущербе на 1 договор: K= 
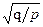, для портфеля из n договоров K=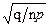 
|
|
|
Если же ущерб распределен, то появляется и второй фактор увеличения опасности для страховщика – большая дисперсия D(Х|А) величины ущерба при наступлении страхового случая, точнее отношение этой дисперсии к квадрату математического ожидания, то есть квадрат условного коэффициента вариации. Эти факторы взаимодействуют (усиливают друг друга). Особую опасность представляют малочисленные очень редкие риски с большим разбросом ущерба.
Именно поэтому в имущественном страховании относительная рисковая надбавка в несколько раз превышает аналогичную в договорах о страховании жизни.
содержание
|
|
|
