 |
Смешанные пуассоновские распределения (пример на Г-распределении)
|
|
|
|
Смешанные пуассоновские распределения (пример на Г-распределении)
На практике параметр пуассоновского распределения λ часто оказывается непостоянным:
- различия параметров пуассоновского распределения у разных страхователей при моделировании числа случаев в индивидуальных моделях;
- различия в параметрах λ для разных лет в портфеле с одинаковыми рисками в случае коллективных моделей (погодные условия, экономическая конъюнктура).
Возникает проблема введения дополнительной СВ Qj, отвечающей за изменение λ и отражающей неоднородность портфеля (в 1-м варианте) или служащей для моделирования ежегодно меняющихся внешних воздействий в однородном портфеле к коллективной модели (2 вариант).
Qj – независимые, одинаково распределенные СВ, характеризующие индивидуальность страхователя в 1-м случае и «качество года» во 2-м случае. Это распределение наз. смешивающим. Итак, плотность распределения СВ Qj будет обозначаться через U(λ ) и называться структурной функцией. Получаемое распределение числа страховых случаев в портфеле называетсая смешанным законом Пуассона:
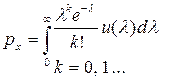
Часто делается конкретное предположение о виде смешивающего распределения, т. е. распределения СВ Qj.
Наиболее распространены в качестве смешивающего:
- гамма-распределение;
СВ имеет Г-распределение (гамма-распределение) с параметрами a и b, если ее функция плотности вероятности имеет вид:
. 
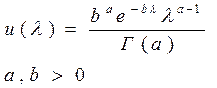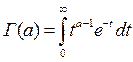- гамма-функция Эйлера. Г(а+1)=аГ(а), Г(а+1)=а! – а – натур. число.
- обратное гауссовское распределение
, M(X)=g, D(X)=g(1+h)
Моделирование совокупного убытка риска и группы рисков.
1-я задача актуариев – моделирование числа убытков (всё выше рассмотренное).
|
|
|
2-я задача – моделирование распределения ущерба в отдельном страховом случае и совокупного убытка по портфелю в целом.
содержание
12. Основные подходы к моделированию ущерба при наступлении страхового случая в одном договоре
Кратко: Основная масса вероятностей сосредоточена в точке 0-го значения убытка по риску, х(i)=0. Распределение с. в. х(i) не имеет непрерывной плотности и далеко от нормального распределения.
С ростом числа независимых и одинаково распределенных рисков стандартизированный совокупный убыток становится похож на нормально распределенную величину. Но ввиду крайней несимметричности распределения х(i) обычно закон работает только при очень большом числе рисков.
Для получения приемлемой аппроксимации распределения убытка малой группы рисков аппроксимируем распределение совокупного убытка х(i) отдельного риска i непрерывным распределением, допускающим явный расчет сверток. Основная масса вероятностей находится в 0.
Самым известным распределением на интервале (0; +∞ ), позволяющим рассчитать свертки в явном виде, является гамма-распределение.
Для моделирования распределения убытка используется гамма-распределение с параметризацией с участием мат. ожидания μ (b=a/μ ):
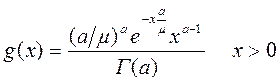
Мат. ожидание М(х)=μ; Дисперсия D(x)=μ 2/a; к-т вариации К=1/√ а; к-т асимметрии Ас=2/√ а
Оценки параметров по выборке по методу моментов:
, 
, а – параметр формы, определяет вид графика плотности вероятности. В актуарных расчетах принимается a< 1.
Сумма независимых гамма-распределенных рисков имеет гамма-распределение, даже если μ i и ai не одинаковы, но постоянно отношение μ i/ai Это позволяет моделировать совокупный убыток группы рисков с разными страховыми суммами.
Одномодальное распределение: μ 0=μ =μ /а
Использование обратного гауссовского распределения для моделирования ущерба в одном договоре.
|
|
|
Плотность распределения:
Мат. ожидание М(х)=μ, Дисперсия D(x)=μ 2/a, к-т вариации К=1/√ а, к-т асимметрии Ас=3/√ а
а – параметр формы, определяет вид графика плотности вероятности. В актуарных расчетах принимается a< 1.
Сумма независимых обр. гаусс. распределенных рисков имеет обратное гауссовское распределение, даже если постоянно отношение μ i/ai Это позволяет моделировать совокупный убыток группы рисков с разными страховыми суммами.
Преимущество: возможность выражения функции распределения через стандартное нормальное распределение и табулированную функцию Лапласа:
Использование логнормального распределения для моделирования ущерба в одном договоре.
Функция плотности вероятности:
Функция распределения логнормальной с. в.:
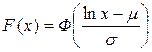
+ используется стандартная ф-ция Лапласа
- Распределение не инвариантно относительно свертки.
Хорошо для моделирования размера убытка в отдельных страховых случаев
Из учебника:
поскольку в коллективной модели убытки не сопоставляются отдельным рискам, а рассматриваются в совокупности на определенном временном промежутке, можно считать, что они представляют собой выборку из одного-единственного распределения, а именно смеси из различных распределений отдельных убытков.
каждому виду страхования и каждому портфелю соответствует свое (смешанное) распределение убытков, зависящее, в частности, от размеров страховых сумм по отдельным рискам, а также от страхуемых событий. Как показывает практика, структуры убытков во всех видах страхования очень схожи. Обычно наблюдается намного больше мелких убытков, чем больших. Строго говоря, «концентрация убытков» с увеличением размера убытка все сильнее уменьшается (бывает, совсем мелкие убытки тоже малочисленны, но с экономической точки зрения они не имеют большого значения). Границы между крупными и мелкими убытками у разных видов страхования различны.
рассмотрим распределения, применимые для моделирования размера убытка.
Логнормальное распределение прекрасно подходит в качестве модели для размера убытка в отдельном страховом случае. Оно имеет плотность
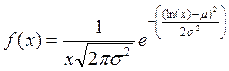
со скалярным параметром b = eµ и параметром формы σ . Логарифмированное правдоподобие
|
|
|
как функция от ln(x) в этом случае представляет собой параболу с ветвями вниз.
Далее. Менее известное, но схожее с нормальным, логистическое распределение имеет плотность
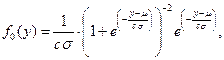
(где 
, µ – математическое ожидание, σ 2 – дисперсия) и функцию распределения
.
В результате преобразования X=exp(Y) получим функцию распределения
,
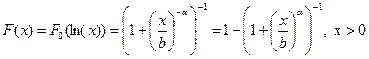где b = eµ (скалярный параметр) и 
. Плотность логарифмированного логистического распределения задается формулой
.
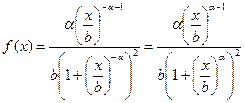Логарифмированное правдоподобие выглядит следующим образом:
.
Симметричной и определенной для всех действительных аргументов плотностью обладает также распределение Лапласа:
,
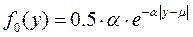состоящее из двух симметричных относительно µ экспоненциальных распределений. Функция распределения Лапласа имеет вид
.
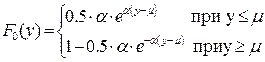После преобразования X=exp(Y) получаем логарифмированное распределение Лапласа (b = eµ):
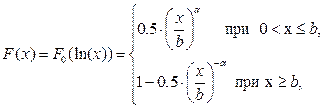
правая часть которого после нормировки известна как распределение Парето. Плотность логарифмированного распределения Лапласа определяется формулой
Правдоподобие:
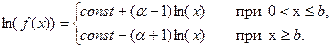
Заметим, что участки малых и средних убытков недостаточно точно аппроксимируются этим распределением, зато в области больших убытков модель приемлема и даже немного переоценивает частоты.
Менее подходящую левую часть (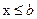 
) логарифмированного распределения Лапласа можно заменить распределением, приемлемым для описания мелких убытков, например, гамма- или обратным гауссовским распределениями. Самый простой способ задать распределение Парето на интервале (0; b) – сместить его влево на величину b. Тогда распределение Парето
превращается в распределение Парето с нулевой точкой:
.
Его плотность и правдоподобие задается функциями:
В некоторых видах страхования распределение Парето с нулевой точкой тоже имеет тенденцию немного переоценивать частоту наибольших убытков. В таких случаях можно заменить преобразование X=exp(Y) на более «слабое» преобразование – X=Yz, z> 1. Тогда из несмещенного экспоненциального распределения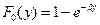 
получается распределение Вейбулла. Однако мы не будем на нем останавливаться.
|
|
|
Мы привели достаточное количество моделей для описания распределения размера убытка в отдельном страховом случае. Распределения с более чем двумя параметрами (например, обобщенное гамма- или обобщенное бета-распределения) не приводились намеренно, т. к. оценивать их параметры значительно сложнее, а значимо лучшего соответствия эмпирическим данным достичь не удается.
содержание
|
|
|
