Резервы заявленных, но не урегулированных убытков. Методы расчета.

Резервы заявленных, но не урегулированных убытков. Методы расчета.

РЗНУ - денежная оценка обязательств страховщика на отчет дату по заявленным, но неурегулированным убыткам, дополнительно учитывающая возврат страховых премий и расходы на урегулирование убытков. РЗУ рассчитывается отдельно по каждой учетной группе. Заявленный, но неурегулированный убыток по всем договорам рассчитывается по формуле:

,

где   - заявлен, но неурегулированный убыток по i договору j учетной группы.

РЗНУ по всему страх портфелю рассчитывается как сумма:

1) заявленных, но неурегулированных убытков по всему страх портфелю ЗУ на отчет дату;

2) всех страх премий, подлежащих на отчет дату возврату страхователям или перестрахователям в связи с досрочным прекращением договоров или изменением их условий (ВПР);

3) расходов по урегулированию убытков по всему страх портфелю, устанавливаемых в размере 3% от суммы заявленных, но неурегулированных убытков и возвращ. премий по всему страх портфелю(ЗУ+ВПР)                       РЗНУ=1, 03(ЗУ+ВПР).

Резервы убытков формируются СК в целях аккумуляции средств по предстоящим страх выплатам, которые определяются на основе уже произошедших страх случаев и убытков, а также на основе их прогноза. В соответствии с законодательством выделяют: резерв заявленных, но неурегулированных убытков (РЗУилиРЗНУ), резерв произошедших, но незаявленных убытков.

Общая идея математических методов - проецировать опыт прошлых лет событий на последующие годы. Требования к данным: отсутствие изломов тренда или структуры (напр, изменение в урегулирование убытков в порядке определения резерва заявленного убытков в политике формирования портфеля и т. д. )

Метод Борнхуеттера-Фергюсона для расчёта резервов произошедших, но не заявленных убытков

1) рассчитывается коэффициенты развития, кот показывают во сколько раз средняя величина убытка, оплаченного в послед периоде развития больше соответствующей величины в предыдущем периоде.

2) рассчитывают факторы развития убытков, которые показывают совокупный результативный темп изменения размера суммарных выплат при переходе от i периода к отчет.

3) определяют фактор запаздывания, который показывает, какая часть убытка урегулиров. на конец i периода и позволяет определить накопленную величину будущих выплат.

4) определяется коэффициент оплаченных убытков - расчетная убыточность по страх случаям i периода

5) определяется среднее значение коэффициента оплаченных убытков - средняя расчетная убыточность

6) расчет ожидаемой величины всех убытков на конец отчетного периода по страховым случаям, наступившим в i пер

7) расчет ожидаемой величины всех неоплаченных убытков к концу отчет квартала по страх случаям, наступившим в i периоде

8) рассчитывается резерв произошедших, но неурегулированных убытков с учетом 3% надбавки на расходы по урегулированию убытков

содержание

20. Построение таблиц смертности. Основные понятия и показатели.

Таблицы смертности представляют собой систематизированный набор статистических данных о продолжительности жизни населения данной страны или выделенной его группы. Выделение групп может проводиться по разным признакам: по полу, региону, профессии и т. п. Во всех случаях таблицы смертности содержат «упорядоченный ряд взаимосвязанных величин, показывающих уменьшение с возрастом вследствие смертности некоторой совокупности родившихся, а также показателей, характеризующих уровень смертности для различных периодов жизни данной совокупности». Таблицы смертности также называют таблицами продолжительности жизни.

В общих таблицах возраст является единственным определяющим параметром (входом таблицы). Общие таблицы дают представление о динамике демографических процессов для всего населения в целом. В специальных таблицах, кроме возраста, учитывается ряд других параметров. Такие таблицы называются таблицами с отбором, или селективными.

В полных ТС показатели даны по возрастам с интервалом в 1 год, в кратких таблицах – с интервалом 5 и 10 лет. ТС могут начинаться с нулевого возраста или же с некоторого данного возраста.

ТС представляет собой набор столбцов, соответствующих различным демографическим показателям. Элементы столбцов упорядочены по возрасту. Первым в ТС, как правило, приводится число людей, доживающих до возраста х: l_x .

Это число относится к фиксированному числу родившихся, обозначаемому l₀ и называемому корнем таблицы смертности. Обычные значения для l₀: 1 млн., 10 или 100 тыс., но оно может быть и произвольным числом. Таким образом, если l₀ = 100000 число родившихся, то l₁ = 98729 означает, что лишь 98729 из них доживут до своего первого дня рождения. ТС заканчиваются строкой, соответствующей предельному возрасту ω .

Другой важной характеристикой, встречающейся в таблицах смертности, является величина d_x, представляющая число умерших в промежутке между годами х и х+1 своей жизни. Таким образом d_x – это число умерших в возрасте х.

Очевидно, что l_x = l_x+1 + d_x, т. к. среди достигших возраста х каждый из них либо достигнет возраста х+1, либо умрет в течение одного года. Эта формула м. б. переписана в виде: l_x+1 = l_x – d_x.

Число q_x можно рассматривать как вероятность умереть в течение одного года (после дня рождения) для человека, достигшего возраста х. Более точно следовало бы говорить, что число q_x (из таблицы смертности) является статистической оценкой этой вероятности. Число q_x называют также уровнем смертности в возрасте х. Таким образом, q_x = d_x / l_x.

Дополнение q_x до 1, т. е. число p_x = 1 – q_x равно доле тех из l_x, достигших возраста х, что доживут до возраста х+1. Эта величина представляет собой условную вероятность прожить еще один год по достижении возраста х.

Поскольку q_x = d_x / l_x, то p_x = 1 – q_x = 1 – d_x / l_x = (l_x – d_x) / l_x = l_x+1 / l_x, т. е. p_x = l_x+1 / l_x.

Соответственно, можно записать: l_x+1 = l_x ∙ p_x или l_x = l_x+1 / p_x= d_x / q_x.

Аналогично: d_x = l_x ∙ q_x

Введем еще ряд вероятностных характеристик, относящихся к более продолжительным периодам.

Число _np_x = l_x+n / l_x равно вероятности прожить еще n лет для лица, достигшего возраста х.

Соответственно число _nq_x = 1 – _np_x = _nd_x / l_x равно вероятности умереть в течение следующих n лет для лица, достигшего возраста х.

Для вероятностей npx выполнены очевидные соотношения: ₂p_x = p_x ∙ p_x+1.; ₃p_x = p_x ∙ p_x+1 ∙ p_x+2.

Имеется много методов построения таблиц смертности. Основное различие этих методов состоит в выборе базового показателя, на основании которого вычисляются все остальные. Чаще всего в качестве базового показателя берется q_x, т. е. вероятность смерти в течение года после достижения возраста х. Этот показатель оценивается исходя из имеющихся статистических данных. Оценив q_x, можно получить все остальные показатели.

Рассмотрим подлежащее и сказуемое таблицы смертности. Подлежащим ТС будет возраст Возрастной интервал берётся от 1 до 100 лет (т. е. ). Сказуемое таблицы состоит из множества граф, опишем каждую из них в отдельности.

1. вероятность умереть в данном возрасте . Рассчитывается на основе реальных (отчётных или официальных) данных и является основой таблицы.

2. Число умирающих в данном возрастном интервале 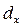, рассчитывается как d_x=l_x*q_x.

3. Число доживающих до данного возраста . Первоначальное значение 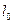 берётся равное 100000 (или10000), а последующие значения рассчитываются по формуле l_x+1 = l_x-d_x      .

4. Функция дожития 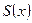, означающая долю лиц из совокупности, доживающих до возраста х [ 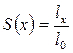].       5. - округленная продолжительность жизни в возрасте х лет [ ].

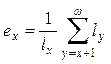1.  - средняя продолжительность жизни, равная 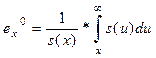 или .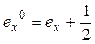

Если же исходными являются не вероятности смерти q_x, а вероятности дожития р_x, то ряд значений для l_x можно получить по формулам l_x+1 = l_x*p_x; d_x = l_x-l_x+1          для α ≤ х ≤ ω.

Вычисленные значения округляются, как правило, до ближайшего целого числа.

Иногда, особенно при построении специальных таблиц, корень таблицы помещается в “середину”, то есть значения α и l_α относятся к “промежуточным”. В этом случае процесс вычисления идет в двух направлениях: к младшим и старшим возрастам. При этом значения l_x и d_x для старших возрастов получаются по формулам, приведенным выше, а для младших возрастов применяются формулы: l_x-1 = l_x/ p_x-1; d_x-1 = _lx-1 - l_x если исходный показатель p_x. Если же в качестве исходного взят q_x, то получив сначала p_x = 1 – q_x, применяют формулы, приведенные выше.

Таким образом, центральным моментом при построении таблиц смертности на основе показателей q_x или p_x является получение их оценки на основании статистических данных. При использовании прямого метода эта оценка строится непосредственно на определении этих вероятностей, например, для q_x по формуле: q_x = d_x / l_x.

Однако непосредственное применение прямого метода наталкивается на значительные трудности. Дело в том, что по самому смыслу этих и других показателей таблицы смертности они относятся к некоторой заданной совокупности лиц, родившихся в одном и том же году. Такие совокупности, образование которых связано с некоторым демографическим событием (рождением, браком и тп. ), в демографии называют когортами. Получение демографических показателей для реального поколения получило в демографии название когортного метода, или продольного анализа.

Коммутационные функции (см вопрос 29)

1. .
2. .
3. .
4. .
5. .
6. . ; .; .

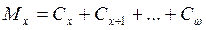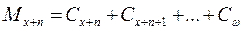содержание

⇐ Предыдущая10111213141516171819Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: