 |
21. Функция дожития – безусловная и условная
|
|
|
|
21. Функция дожития – безусловная и условная
Актуарные расчеты в страховании жизни опираются на предварительно построенную функцию дожития. Кривая дожития строится на основе реальных отчетных данных. Функция дожития базируется на отношении числа умерших в каждой возрастной группе к числу доживших до этого возраста на начало рассмотренного периода.
Функция S(x) = 1 – F(x) называется функцией дожития или выживания: S(x) = P (X> x)
Вот некоторые свойства этой функции:
S(x) убывает. В противном случае существовал бы фиксированный неслучайный период в жизни людей, когда смерть невозможна.
S(0) = 1; S(+∞ ) = 0
S(x) непрерывна справа, в противном случае существовал бы некоторый фиксированный момент в жизни человека, в котором он умирал бы с положительной вероятностью.
S(x) характеризует среднюю долю живых представителей некоторой фиксированной группы новорожденных к моменту х: S(x) = lx / lo.
Рассмотренная выше функция дожития представляет собой безусловную вероятность или безусловную функцию дожития.
Статистические свойства времени жизни людей, доживших до определенного возраста х, существенно отличаются от свойств времени жизни новорожденного. В связи с этим, в страховой практике для человека в возрасте х лет обычно рассматривают не продолжительность жизни, а остаточное время жизни: Tx = T – x. Тогда функция распределения будет иметь следующий вид:
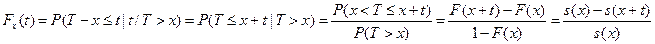
Исходя из этого выражения, мы можем выразить функцию дожития:
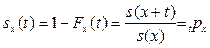
Таким образом, мы получили условную функцию дожития, представляющая собой вероятность tpx (вероятность того, что человек возрасте х лет проживет еще по крайней мере t лет).
содержание
22. Функция распределения продолжительности предстоящей жизни и её связь с функцией дожития
|
|
|
В теории вероятностей стохастическую природу любой случайной величины х описывает функция распределения F(x). Она определяется, как вероятность того, что случайная величина Х не больше, чем число х: 
. Применительно к актуарным расчетам, F(x) – этофункция распределения продолжительности жизни, онабудет означать вероятность того, что человек не доживет до возраста х лет.
В актуарной математике принято работать с дополнительной функцией распределения: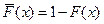 
, которая указывает вероятность того, что случайная величина Х больше, чем некоторое число х. Говоря про продолжительность жизни, это вероятность того, что человек доживет до возраста х лет.
Функция S(x) = 1 – F(x) называется функцией дожития или выживания: S(x) = P (X> x).
содержание
23. Интенсивность смертности и её связь с функцией дожития
Кроме характеристики смертности за отдельные периоды времени абсолютными величинами необходимо иметь информацию о доле числа умерших по отношению к числу живых в начале исследуемого периода. Т. е. информацию о вероятности смерти в течение ближайшего времени. Условная вероятность смерти человека, достигшего возраста x лет в промежутке от x до (x+t) определяется как:
Если рассмотреть единицу времени (год жизни) в этом промежутке, то доля умерших в течение очень маленького интервала времени характеризует скорость вымирания лиц, достигших определенного возраста x лет. Если t мало, то, переходя к пределу, получим:
Сила смертности:
Данная величина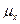 
называется силой смертности (интенсивность смертности) в возрасте x лет и является важной характеристикой процесса вымирания определенной группы населения.
Определение интенсивности смертности можно рассматривать как дифференц. отношение относительно s(x), т. к. имеет место
Интенсивность смертности может быть использована в качестве первичной характеристики продолжительности жизни (поскольку функция выживания s(x) может быть восстановлена по интенсивности смертности)
|
|
|
Представление о характере зависимости 
можно получить из таблицы смертности. Наряду с другими характеристиками продолжительности жизни в ней (в табл. смертности) протабулирована функция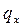 
.
, 
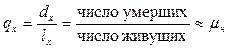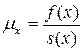
где 
, 
(если рассматривается маленький промежуток времени)
Свойства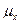 
:
1) 
2) 
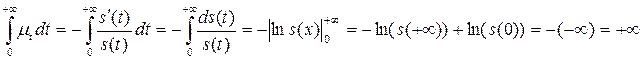
Данные свойства являются характеристическими.
содержание
|
|
|
