Оценивание параметров системы одновременных уравнений

Кратко рассмотрим проблему оценивания параметров системы одновременных уравнений, учитывая их специфику. В системах одновременных эконометрических уравнений одни и те же переменные одновременно выступают в одних уравнениях как экзогенные, а в других – как эндогенные. Поэтому оценивать их обычным МНК не представляется возможным в связи с тем, что в них не выполняется предпосылка независимости регрессоров и остатков.

Один из методов преодоления этой проблемы заключается в том, что структурную форму модели записывают в виде приведённой формы, выражая эндогенные переменные через экзогенные. Приведённая форма модели представляет собой систему не связанных друг с другом уравнений, которые можно по отдельности оценить обычным МНК. Затем оценки параметров этих уравнений используются для вычисления оценок параметров структурной формы модели. Такой подход называется косвенным МНК. Но он не всегда может быть реализован, т. к. нет гарантии, что через оценки параметров приведённой формы модели можно будет однозначно определить оценки параметров структурной формы модели.

Обычно параметры приведённой формы являются нелинейными функциями параметров структурной формы, и не ясно, представляют ли параметры приведённой формы достаточную информацию, чтобы идентифицировать все структурные параметры. Это известная проблема идентифицируемости в моделях одновременных уравнений. Здесь не будем обсуждать идентифицируемость в контексте вывода структурных параметров из параметров приведённой формы. Вместо этого рассмотрим проблему идентифицируемости как проблему поиска достаточного числа инструментальных переменных для эндогенных переменных модели.

Вернёмся к кейнсианской модели. Как уже отмечалось, при оценивании параметров уравнения функции потребления обычным МНК «мешает» тот факт, что в правой части этого уравнения находится эндогенная переменная, коррелированная с остатком этого уравнения. Одним из методов решения этой проблемы является использование для этой переменной инструмента. На этой идее и основывается другой метод оценивания параметров структурной формы модели, который при определённых условиях является более общим, чем косвенный МНК и в частном случае (при точно идентифицируемых системах) даёт одинаковые результаты с косвенным МНК.

В этом случае проблема состоит в том, чтобы найти подходящие инструментальные переменные. В большинстве случаев это требует знания экономической теории. В полной модели одновременных уравнений эта проблема решаема, поскольку любая экзогенная переменная, которая не включена в соответствующее уравнение, может использоваться в нём в качестве инструментальной переменной. Более точно любую экзогенную переменную, которая имеет влияние на эндогенный регрессор, можно использовать в качестве инструмента при условии, что она не включена в оцениваемое уравнение.

Для кейнсианской модели это означает, что инвестиции обеспечивают адекватную инструментальную переменную для доходности .

Реализуется это следующим образом. Сначала оценивается уравнение регрессии = + + _t, затем по этому уравнению рассчитываются прогнозные значения зависимой переменной и эти значения используются в дальнейшем при оценивании параметров уравнения функции потребления. Т. е. вместо уравнения = 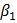+ + 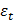будем оценивать уравнение = 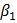+ + 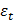, заменив реальные значения доходностей их расчётными значениями , тем самым обеспечив независимость регрессора и остатков.

Как видим, здесь пришлось дважды применить МНК: один раз для вычисления прогнозных значений доходностей и второй раз – для оценки параметров основного уравнения модели, поэтому такой метод и получил название двухшагового МНК.

В общем случае, когда в уравнении системы одновременных эконометрических уравнений имеется несколько эндогенных объясняющих переменных, в качестве инструментальных переменных для них могут служить экзогенные переменные из других уравнений системы. Поэтому в системе одновременных эконометрических уравнений должно быть доступно достаточное число инструментальных переменных. Это и составляет проблему идентифицируемости параметров структурной формы модели.

Практическая реализация двухшагового МНК осуществляется следующим образом. Сначала МНК оценивает приведённую форму (т. е. регрессию эндогенных регрессоров на все инструментальные переменные). На втором шаге МНК оценивает исходные структурные уравнения после замены всех эндогенных переменных в правой части одновременной системы уравнений их прогнозными значениями из приведённой формы.

 

Пример 7. Инструментальные переменные

Проиллюстрируем применение инструментальных переменных на примере.

Рассмотрим использование метода инструментальных переменных, реализованный в эконометрическом пакете программ EViews (EViews 7 User's Guide II). Оценим уравнение регрессии, в котором выражена зависимость спроса на сигареты (packpc) от индиваидуального совокупного дохода (perinc) и цены за одну пачку сигарет (ravgprs). Сначала оценим эту зависимость, используя обычный МНК (рисунок 3.1), предполагая, что обе независимые переменные экзогенные, т.е. что они не коррелируют с ошибками.

 

 

Рисунок 3.1 – Отчёт о регрессии без инструментов

 

 

Рисунок 3.2 – Тест Рамсея RESET для исходного уравнения

 

Тест Рамсея показал (рисунок 3.2), что в этом уравнении есть ошибка спецификации (вероятность для F-статистики равна 0,02, что 0,05). Вслед за автором примера будем считать, что переменная (ravgprs) эндогенная и выберем для неё в качестве инструментов средний налог на продажу (rtacso) и специальный налог на сигареты (rtacs). Рассчитаем уравнение регрессии зависимости эндогенной переменной ravgprs от этих двух переменных. Получим (рисунок 3.3).

 

 

Рисунок 3.3 – Расчёт инструмента

 

Как показывает коэффициент множественной детерминации (он равен 0,93), зависимость между этими переменными тесная и расчётное значение ravgprsf можно использовать в качестве инструмента для ravgprs. Сохраним в рабочей области ravgprsf процедурой Proc / Forecast…, а затем заменим этой переменной в уравнение регрессии ravgprs. Такой приём называется очищением эндогенной переменной от коррелированности с остатками. Получим уравнение (рисунок 3.4).

 

Рисунок 3.4 – Уравнение регрессии с инструментом ravgprsf

 

 

Рисунок 3.5 – Тест Рамсея для уравнения с инструментом

 

По сравнению с исходным уравнением коэффициент при инструментальной переменной изменился незначимо, а значимое различие оценки при переменной perinc не существенно, т. к. обе оценки (в исходном уравнении и в уравнении с инструментом) не значимо отличны от нуля. Тест Рамсея (рисунок 3.5) показывает теперь, что ошибки спецификации в этом уравнении нет (Probability для F-статистики равна 0,19, что больше 0,05).

По сути дела, проделав эту процедуру, мы применили двухшаговый МНК, проведя оба шага «вручную».

Рассмотрим этот же метод, реализованный в EViews программно.

Как и ранее, будем считать, что цена на сигареты является эндогенной переменной, и в качестве инструментальных переменных для этой переменной возьмём средний налог на продажу (rtacso) и специальный налог на сигареты (rtacs). Переменная perins предполагается экзогенной, следовательно, она будет инструментировать саму себя и поэтому включается в список инструментов. Кроме того, в качестве инструмента всегда выбирается константа.

Откроем эти переменные как группу и выберем Proc / Make Equation…. В открывшемся диалоговом окне выберем в позиции Method: TSLS (двухшговый МНК), заполним позиции «Equation specification – спецификация уравнения» и «Instrument list – список инструментов» в соответствии с рисунком 3.6 и щёлкнем «OK».

 

 

Рисунок 3.6 – Спецификация двухшагового МНК

 

В результате получим отчёт о решении (рисунок 3.7). Как видно из отчёта, в нём кроме стандартных характеристик уравнения перечислены инструментальные переменные и указан ранг матрицы инструментов (он равен числу инструментов), а также сумма квадратов остатков для первого шага (Sum squared resid) и для второго шага (Second-Stage SSR).

 

 

Рисунок 3.7 – Отчёт о двухшаговом МНК в EViews

 

Сравнение этого результата с результатом, полученным «ручным» способом (рисунок 3.4) показывает, что они почти не различаются кроме незначимой оценки параметра при переменной perins.

Пример 8. Оценка системы одновременных эконометрических уравнений

Рассмотрим более сложный пример использования инструментальных переменных. Проиллюстрируем оценку параметров системы одновременных уравнений двухшаговым МНК с помощью EViews.

Для этого воспользуемся объектом пакета EViews «System-система». С помощью этого объекта можно создать систему одновременных уравнений, и оценить её параметры. В объекте «System» двухшаговый МНК является одним из возможных методов оценивания параметров системы одновременных уравнений.

Рассмотрим следующую простую модель экономики

cn_t = c₁ + c₂ y_t + c₃ cn_t-1 + e_t;

i_t = c₄ + c₅ y_t + c₆ cn_t-1 + u_t;

y_t = cn_t + i_t + g_t.

Здесь cn_t – индивидуальное потребление в году t;

i_t – инвестиции в году t;

y_t – валовой внутренний продукт в году t;

g_t – государственные расходы в году t.

Имеем систему двух одновременных уравнений и тождество.

Оценим параметры этой системы, при помощи объекта System, с использованием двухшагового МНК.

С этой целью создадим объект «система», в котором специфицируем эти уравнения. Для этого воспользуемся одним из вариантов, выбрав Objekt / New Object…/ System. Появится пустое окно объекта «система», которое нужно заполнить спецификацией одновременных уравнений (тождество на данном этапе не вводится). Кроме того, поскольку для оценки параметров системы предполагается применить двухшаговый МНК, в конце каждого уравнения вводится список инструментов (список инструментов можно вводить в конце каждого уравнения после знака @). В этом примере предполагается, что эндогенные переменные – это cn, y и i, а переменная g и лаговые значения переменных – экзогенные переменные (константа автоматически вводится в уравнения инструментов, а потому в списках инструментов её нет). Тождество также не вводится в окно «системы». Получим (рисунок 3.8) (список инструментов подбирался исходя из профессионально-логических соображений).

 

 

Рисунок 3.8 – Окно спецификации системы одновременных уравнений

 

Чтобы оценить параметры системы, нужно щёлкнуть в этом окне в меню кнопку Estimate и выбрать метод оценки в диалоговом окне System Estimation. Для этого в заставке Estimation Method выбираем двухшаговый МНК (Two-Stage Least Squares) (рисунок 3.9).

 

 

Рисунок 3.9 – Выбор метода оценивания

 

Поскольку и в модели и в инструментах имеются лаговые значения переменных, необходимо их обеспечить соответствующими наблюдениями, указав в окне оценки системы соответствующее начало выборки, сместив его на один год вперёд. В нашем примере есть переменные cn_t-1 и i_t-1, а выборка начинается с 1960q1, следовательно, в окне System Estimation надо указать начало выборки как это показано ниже (вместо 1960q1 надо проставить 1961q1) (рисунок 3.10).

 

Рисунок 3.10 – Установка начала выборки

 

Щёлкнув после этого ОК, получим отчёт об оценке параметров системы одновременных уравнений двухшаговым МНК, как это указано на рисунке 3.11.

 

 

Рисунок 3.11 – Отчёт об оценке параметров системы одновременных уравнений

 

Итак, имеем (с округлениями)

cn_t =-12,5 + 0,067 y_t + 0,91 cn_t-1 + e_t,

i_t = -356,3 + 1,02 y_t + -1,24 cn_t-1 + u_t,

Как видим, в отчёте поотдельности указаны оба уравнения, для каждого из них инструменты, оценки их параметров и некоторые показатели точности. Кроме того, как и обычно, можно воспользоваться опциями в меню и просмотреть графики остатков для каждого уравнения, анализ самих остатков и т. д.

Если оценить каждое уравнение по отдельности обычным МНК, то получим иной результат (рисунки 3.12 и 3.13).

 

 

Рисунок 3.12 – Оценка параметров первого уравнения системы обычным МНК

 

Рисунок 3.13 – Оценка параметров второго уравнения системы обычным МНК

А если применить двухшаговый МНК в «ручном» варианте, то результат оценки в этом случае мало отличается от оценки в объекте «System» (см. рисунки 3.14 и 3.15, где YF рассчитано из уравнения инструмента: yf_t = a+b₁y_t+b₂cn_t-1+e_t).

 

 

Рисунок 3.14 – Оценка параметров первого уравнения системы двухшаговым МНКв «ручном» варианте

 

 

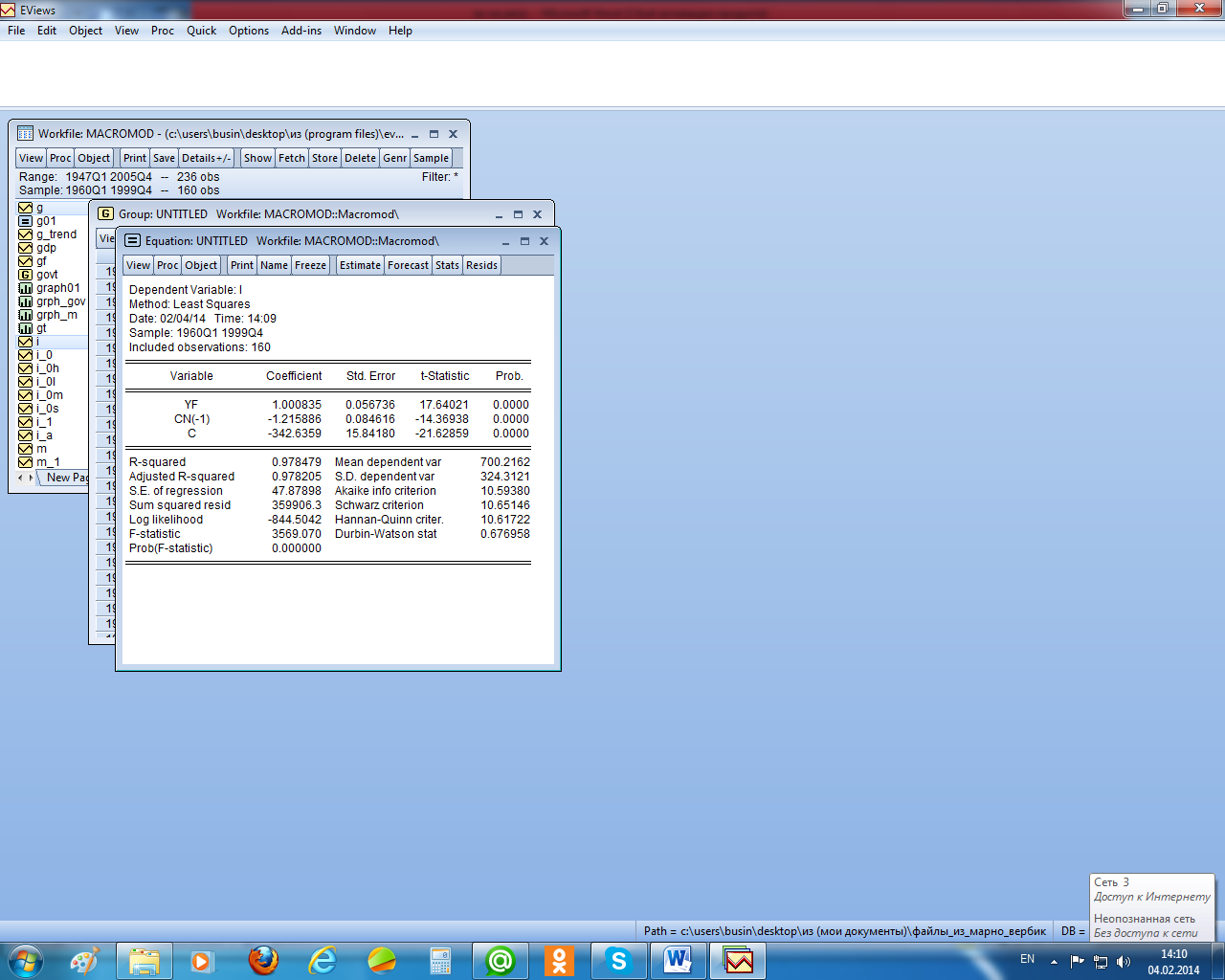
Рисунок 3.15 – Оценка параметров второго уравнения системы двухшаговым МНК в «ручном» варианте

 

 

⇐ Предыдущая891011121314151617

Поделиться:

Воспользуйтесь поиском по сайту: