 |
Проективное определение конического сечения
|
|
|
|
Теорема
Если вокруг окружности (конического сечения) описан четырехвершинник, то прямые, соединяющие точки касания противоложных сторон, и диагонали четырехвершинника пересекаются в одной точке.
Эту теорему, конечно же, возможно доказать обычным образом, используя подобие треугольников. Кроме того в дальнейшем будет доказана теорема Брианшона, для которой теорема об описанном четырехвершиннике является естественным частным случаем.
Попробуем теперь применить доказанные теоремы для исследования свойств гиперболы. Напомним, что гиперболой называется коническое сечение, пересекающее бесконечно удаленную прямую. Касательные в двух бесконечно удаленных точках называются асимптотами гиперболы.
На евклидовой плоскости гипербола и окружность – это две различные кривые второго порядка. С проективной точки зрения между ними нет никакой разницы. Они просто по-разному расположены по отношению к наблюдателю. Все проективные свойства окружности будут также и проективными свойствами гиперболы, параболы и эллипса.
Пусть асимптоты гиперболы пересекаются в точке Р, полюсе бесконечно удаленной прямой. Проведем касательную в произвольной точке М. Эта касательная пересекает поляру точки Р и две касательные, проведенные из точки Р, в точках А, В, К таких, что АВ, МК – гармоническая четверка (почему? ). Это верно для любой точки Р, лежащей вне конического сечения.
Но если точка К является бесконечно удаленной, то точка М, как известно, будет серединой отрезка АВ. Получаем теорему:
Отрезок касательной к гиперболе, отсеченный асимптотами, делится точкой касания пополам.
Еще одно важное свойство гиперболы можно получить с помощью теоремы об описанном четырехвершиннике.
|
|
|
Рассмотрим четырехвершинник ABCD, сторонами которого являются две касательные и две асимптоты (тоже касательные). В силу доказанной теоремы, прямые АС и BD пересекаются в точке, лежащей на прямой, соединяющей точки касания гиперболы с прямыми AD и ВС, то есть в бесконечно удаленной точке.
Это означает, что прямые АС и BD параллельны. Следовательно, площади треугольников АВС и ADC равны, откуда следует равенство площадей треугольников АВР и СDР. Значит верна теорема:
Треугольник, образованный асимптотами гиперболы и произвольной касательной, имеет постоянную площадь.
Проективное определение конического сечения
Определение конического сечения как центральной проекции окружности не является, увы, вполне «проективным». Во-первых, в этом определении задействована окружность. Определение же окружности как множества точек равноудаленных от центра не относится к проективной геометрии. Во-вторых, возникает естественный вопрос: является ли центральная проекция конического сечения также коническим сечением?
Действительно, рассмотрим проекцию окружности на какую-либо плоскость. Эту проекцию мы назвали коническим сечением (коникой). Теперь построим проекцию этой коники на другую плоскость. Является ли новая проекция также коническим сечением? Или, точнее говоря, можно ли рассматривать ее как центральную проекцию какой-нибудь подходящей окружности?
Для того, чтобы дать утвердительный ответ на этот вопрос, вспомним другое определение окружности. Возьмем на евклидовой плоскости две произвольные точки А и В. Окружностью назовем геометрическое место точек М таких, что направленный (! ) угол Ð АМВ является постоянным и равным a. Направленный угол понадобился, чтобы, во первых, не говорить про углы a и 180° – a, а во-вторых, чтобы не удвоить окружность.
|
|
|
Если теперь взять на окружности четыре точки A, B, C, D, то для любой точки М, лежащей на окружности, сложное отношение прямых (MA MB, MC MD) будет одним и тем же. Это следует из того, что вписанные углы, опирающиеся на одну дугу, равны, а сложное отношение четверки прямых выражается через синусы углов между ними.
Можно рассмотреть отображение пучка прямых, проходящих через точку М, на пучок прямых, проходящих через точку N. Соответственными прямыми будем считать те прямые, точка пересечения которых лежит на окружности. Это отображение является проективным, поскольку сложное отношение прямых сохраняется.
Теперь можно дать проективное определение конического сечения без использования окружности.
Рассмотрим на проективной плоскости два пучка прямых вместе с проективным отображением одного пучка на другой. Если отображение не является перспективным, то точки пересечения соответственных прямых двух пучков не лежат на одной прямой.
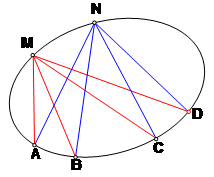Оказывается, эти точки пересечения обязательно лежат на какой-нибудь конике. Более того, это можно считать ее определением. Назовем коникой множество точек пересечения соответствующих прямых двух пучков, между которыми установлено проективное соответствие.
Ясно, что данное определение включает в себя окружность, как частный случай и, кроме того совершенно очевидно, что центральная проекция коники снова является коникой, поскольку при проекции сложные отношения сохраняются.
Осталось показать, что это определение совпадает с исходным, а именно, каждая коника (в смысле нового определения) является центральной проекцией какой-либо подходящей окружности.
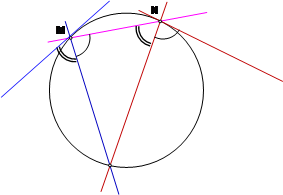Заметим сначала, что поскольку в случае окружности отображение пучка на пучок попросту сохраняет углы между прямыми, то прямой, соединяющей вершины пучков, соответствует при отображении касательная к окружности. Если рассматривать общую прямую MN, как принадлежащую пучку с вершиной М, то ей соответствует касательная в точке N, и наоборот.
Таким образом, чтобы задать два пучка, порождающих окружность, нужно провести всего пять прямых. Разумеется, три прямые, проходящие через точку М, можно выбирать произвольным образом. Затем на одной из них выберем точку N и проведем через нее еще две прямые, так чтобы соответственные углы оказались равными (см. чертеж).
|
|
|
Получаем по три прямых в каждом пучке, поскольку прямая MN входит в оба пучка сразу. Этого как раз хватает, чтобы задать проективное отображение одного пучка на другой. Для любой прямой из одного пучка можно теперь построить ее образ в другом пучке.
Это уже было сделано ранее одним способом, когда отображение пучков было представлено в виде композиции двух перспективных отображений. Впоследствии мы рассмотрим и другой способ, хорошо работающий в данном конкретном случае.
Перейдем теперь к случаю произвольной коники. Рассмотрим проективное отображение пучка a с вершиной М на пучок b с вершиной N. Общую прямую MN назовем l. Если бы прямая l при отображении оставалась на месте, то по доказанной теореме точки пересечения соответственных прямых из двух пучков лежали бы на оси перспективы.
Поскольку мы рассматривем отображение, не являющееся перспективным, то прямая l является образом прямой m из пучка a, а ее образ – это прямая n из пучка b. (Для окружности прямые m и n были касательными в вершинах пучков, они же будут касательными и к конике. ) Выберем еще в пучке a любую прямую а, а в пучке b – ее образ b. Точку пересечения прямых а и b назовем А. Проективное отображение полностью задается тремя парами соответственных элементов. В первом пучке возьмем прямые m, a, l, а в другом – их образы l, b, n.
Проведем через прямую n любую плоскость и построим в ней окружность, которая касается прямой n в точке N. Проведем касательную m' к окружности, проходящую через точку пересечения прямых m и n. Точку касания обозначим М'. Через прямую a и точку М' проведем плоскость, пересекающую окружность в точках М' и А'. Точку S пересечения прямых АА' и ММ', лежащих в одной плоскости, сделаем центром проекции.
Рассмотрим проекцию плоскости окружности на исходную плоскость с центром S. Точки М', А', N переходят в точки М, А, N. В плоскости окружности можно рассмотреть проективное отображение пучка с вершиной М' на пучок с вершиной N. Точки пересечения соответственных пучков порождают окружность. Соответствующее отображение пучков задается соответствием троек прямых m', a', l' и l', b', n. Эти прямые являются прообразами прямых m, a, l и l, b, n при центральной проекции. Значит, соответственные лучи пучков, порождающих окружность, переходят при проекции в соответственные лучи пучков, порождающих конику. Что и требовалось доказать.
|
|
|
|
|
|
