 |
Задача о бабочке. Проективные отображения конических сечений
|
|
|
|
Задача о бабочке
Мы уже неоднократно сталкивались с тем, что проективная геометрия служит источником разнообразных сложных задач по планиметрии. Вот еще одна знаменитая задача про окружность, известная как «задача о бабочке».
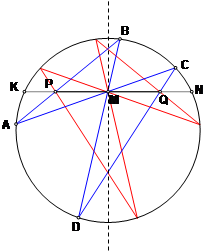
Пусть хорды окружности АС, BD и KN пересекаются в точке М, а прямая KN пересекает прямые АВ и CD и точках Р и Q. Если точка М является серединой хорды КМ, то MP = MQ.
Все известные «школьные» решения этой задачи довольно сложны. Дело в том, что в основе ее лежит проективная теорема, поэтому использовать в решении такие свойства окружности, как равенство радиусов или равенство вписанных углов, напрямую не получается. Приходится изобретать неочевидные дополнительные построения и всячески «выкручиваться». Если же перевести задачу на «проективный язык», решение становится вполне прозрачным.
Вместо окружности возьмем произвольную конику. Точка М пусть будет не серединой хорды, а произвольной точкой на некоторой прямой. На нашем чертеже эта прямая пересекает конику, хотя это совсем не обязательно. Выберем на прямой l еще одну точку Р и проведем через нее какую-нибудь прямую, пересекающую конику в точках А и В. Теперь проведем прямые АМ и ВМ до пересечения с коникой в точках С и D. Пусть прямая CD пересекает прямую l в точке Q.
Оказывается, положение точки Q на прямой l определяется только коникой и точками М и Р. «Бабочка» ABCD может быть любой (! ), лишь бы сторона АВ проходила через точку Р, а прямые АС и BD пересекались в точке М.
Чтобы убедиться в этом построим полный четырехвершинник с вершинами A, B, C, D, который позволяет провести поляру m точки М. Пусть эта поляра пересекает прямую l в точке К. Положение точки К на прямой l зависит только от коники и точки М.
|
|
|
На стороне четырехвершинника АD образовалась гармоническая четверка АD, XY. Ее проекцией на прямую l является четверка КМ, PQ. Значит, точка Q – это четвертая гармоническая к точкам М, К, Р, положение которых не зависит от «бабочки» ABCD.
Другими словами:
Пусть четыре прямые пучка с вершиной М пересекают конику в точках АВ, CD, А'В', C'D', прямые АD и A'D' пересекаются в точке Р, прямые ВС и В'С' – в точке Q. Тогда точки Р, Q, М лежат на одной прямой.
Это утверждение можно также вывести, используя теорему Паскаля. Возвратимся теперь к задаче о бабочке.
Проведем через точку М серединный перпендикуляр к отрезку KN и построим «бабочку», симметричную исходной. Точки Р и Q пересечения соответственных сторон двух «бабочек», во-первых, симметричны относительно проведенной оси, а во-вторых, лежат на одной прямой с точкой М. Отсюда сразу же получаем утверждение задачи.
 |
Проективные отображения конических сечений
До сих пор мы рассматривали проективные отображения прямой на прямую и пучка на пучок. Попробуем рассмотреть отображение коники на конику или, что более важно, отображение коники самой на себя. Для этого надо лишь определить сложное отношение четырех точек коники или четырех касательных к конике.
Это определение естественным образом следует из ранее доказанных теорем. Возьмем на коническом сечении четыре произвольные точки A, B, C, D и пятую точку М. Как нам уже известно, сложное отношение прямых МA, МB, МC, МD не зависит от выбора точки М. Назовем это отношение сложным отношением четырех точек коники.
Точно так же, выбирая четыре касательные a, b, c, d и пятую касательную m, называем сложным отношением четырех касательных a, b, c, d сложное отношение точек их пересечения с прямой m. Это сложное отношение не зависит от выбора касательной m. Более того, сложное отношение четырех касательных равно сложному отношению точек касания. Это следует из того, что при полярном отображении точки коники переходят в ее касательные и наоборот, а все сложные отношения сохраняются.
|
|
|
В дальнейшем имеет смысл рассматривать невырожденную конику, как совокупность всех ее точек и, одновременно, всех ее касательных. Можно тогда без оговорок считать, что полярное преобразование конику переводит в конику. Точки и прямые при этом меняются местами.
Можно теперь рассмотреть отображение коники самой на себя, сохраняющее сложное отношение четырех точек (касательных). Если точки A, B, C, D переходят в точки A', B', C', D', то (AB, CD) = (A'B', C'D') (аналогично для касательных). Такое отображение назовем проективным. Оказывается, проективные отображения «хорошо устроены», то есть обладают многими полезными свойствами.
Покажем, во-первых, что проективное отображение коники на себя задается тремя точками и тремя их образами. Если известно, что точки A, B, C переходят в точки A', B', C', то образ D' любой другой точки D однозначно определен.
Заметим сначала, что поскольку сложное отношение четырех точек коники определено через сложное отношение четырех прямых, то для любых трех точек коники и заданного значения сложного отношения существует единственная точка, для которой это отношение принимает данное значение. Покажем теперь, как построить эту точку.
Рассмотрим два пучка с вершинами А и А'. Проведем прямую s через точки пересечения прямых АВ', А'В и АС', А'С. Построим перспективное отображение одного пучка на другой с осью перспективы s. Каждой прямой каждого пучка соответствует единственная точка коники. При этом точки А и А' соответствуют касательным в своих пучках. Отображение пучка на пучок задает отображение коники самой на себя. Сложное отношение, конечно же, сохраняется.
Значит образ D' точки D строится так:
Проводим прямую А'D до пересечения с осью s, затем соединяем получившуюся точку с точкой А и продолжаем до пересечения с коникой в точке D'.
Главное свойство проективного отображения коники на себя состоит в том, что положение оси перспективы s не зависит от выбора двух соответственных точек А и А'. Ось перспективы задается самим отображением.
|
|
|
Пусть задано проективное отображение коники на себя. Выберем любую пару точек А, В и их образов А', В'. Точки пересечения прямых АВ' и А'В лежат на одной прямой. Эта прямая s называется осью перспективы отображения коники на себя.
Для доказательства достаточно взять на конике три любые точки A, B, C и их образы A', B', C' и убедиться, что точки пересечения пар прямых АВ' и А'В, АС' и А'С, ВС' и В'С лежат на одной прямой. Это утверждение есть не что иное, как хорошо знакомая нам теорема Паскаля. Значит, для любого отображения коники задана его ось.
На нашем чертеже ось s не пересекает конику. Если же это не так, то точки пересечения коники с осью будут неподвижными точками отображения. (почему? ) Кроме того, любое отображение можно задать парой соответственных точек А и А' и осью s.
|
|
|
