 |
Теорема Понселе. Центральное отображение
|
|
|
|
Теорема Понселе
Свойства проективных отображений позволяют доказать теорему Понселе для треугольников. Сформулируем ее пока что следующим образом:
Если вершины двух трехвершинников принадлежат некоторой конике, то все их шесть сторон касаются другой коники.
Для доказательства рассмотрим два трехвершинника АВQ и CDP. Пусть стороны РС и PD пересекают прямую АВ в точках К и L, а стороны QA и QB пересекают прямую CD в точках M и N.
Сложное отношение четырех точек коники определяется через сложное отношение четырех прямых. Рассматривая пучок с центром в точке Р, получаем, что
(АС, DB) = (AK, LB). Точно так же рассматривая пучок с центром в точке Q, получаем, что (АС, DB) = (MС, DN). Следовательно, (AK, LB) = (MС, DN), и, значит, существует проективное отображение прямой АВ на прямую CD, при котором точки A, K, L, B переходят в точки M, С, D, N. Прямые, соединяющие соответственные точки отображения, принадлежат оболочке некоторой коники, что и требовалось доказать.
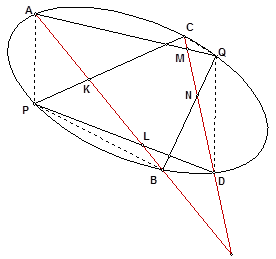Заметим, что любая коника полностью задается пятью своими касательными. Рассмотрим какой-либо трехсторонник, стороны которого касаются коники Γ 1, а вершины лежат на конике Γ 2. Если взять теперь любой трехсторонник с вершинами, лежащими на Γ 2, и двумя сторонами, касающимися Γ 1, то из доказанной теоремы следует, что и третья его сторона обязательно будет касаться той же самой коники Γ 1.
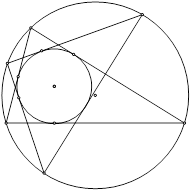Для двух окружностей теорему Понселе можно сформулировать так:
Пусть a и b – вписанная и описанная окружности одного и того же треугольника. Тогда для любой точки М, лежащей на окружности b, существует треугольник с вершиной М, вписанный в окружность b и описанный вокруг окружности a.
Центральное отображение
|
|
|
Важный случай проективного отображения коники на себя – центральное отображение. Строится оно следующим образом:
Возьмем любую точку S, не лежащую на конике и рассмотрим пучок с вершиной S. Если прямая пучка пересекает конику в точках А и А', то будем считать, что точки А и А' переходят друг в друга при центральном отображении с центром S. Если же прямая пучка касается коники в точке Р, то будем считать, что точка Р переходит сама в себя.
Докажем, что центральное отображение является проективным, а его ось – это поляра точки S.
Заметим сначала, что если прямые АА' и ВВ' пересекаются в полюсе S, то точки пересечения прямых АВ', А'В и АВ, А'В' лежат на поляре s.
Построим теперь отображение, заданное парой соответственных точек А, А' и осью s. Для любой точки В ее образ В' строится так:
Построим точку Р пересечения прямой А'В с осью s. потом проведем прямую АР до пересечения с коникой в точке В'. Нетрудно заметить, что поскольку ось s является полярой точки S, то прямая ВВ' проходит через полюс S. Более того, то же самое построение, будучи примененным к точке В', приведет обратно к точке В.
Значит, проективное отображение, заданное парой точек А, А' и осью s, совпадает с центральным отображением с центром S.
Точно так же несложно доказать, что если при проективном отображении коники хотя бы одна пара точек меняется местами, то отображение является центральным. Доказательство можно провести на том же самом чертеже.
Действительно, если точка А' является образом точки А, и одновременно, точка А является образом точки А', то построение точки В' по известной точке В можно вести двумя способами.
Можно строить прямую А'В, находить точку Р ее пересечения с осью, потом проводить прямую АР до пересечения с коникой в точке В'. Но можно идти и в обратном порядке. Построим точку Q пересечения прямой АВ с осью s. потом проведем прямую А'Q до пересечения с коникой в точке В'. Чтобы построение двумя способами привело к одной и той же точке В', прямая АА' должна обязательно проходить через полюс S оси s. Но в этом случае, как мы уже видели, отображение является центральным.
|
|
|
Используя доказанные свойства, решим интересную задачу.
|
|
|
