Система массового обслуживания как модель

С истемы массового обслуживания (англ. queuing system)называют Q- схемами. Под СМО понимают динамическую систему, предназначенную для эффективного обслуживания случайного потока заявок при ограниченных ресурсах системы. Обобщённая структура СМО приведена на ИСнке 2.1.

Если поступающий поток заявок поступает обслуживается несколькими параллельно включенными

В многоканальной СМО (многоканальная Q-схема) поступающие заявки обслуживаются любым из параллельно включенных каналов (приборов) обслуживания. В многофазной СМО заявка проходит обслуживание несколькими последовательно включенными каналами обслуживания.

При многоканальном обслуживании (многоканальная Q-схема), и многофазное обслуживание (многофазная Q-схема).

Q - схемы можно исследовать аналитически и имитационными моделями.

 

Рис. 2.1. Схема многоканальной СМО.

В любом элементарном акте обслуживания - две основные составляющие: ожидание заявкой обслуживания и собственно обслуживание заявки.

Рис. 2.2. Схема одноканальной СМО

 

На каждый элемент СМО поступают потоки событий: в накопитель H_i поток заявок w _i, на канал обслуживания K_i – поток обслуживания u _i.

 

Потоком событий (ПС) называется последовательность событий, происходящих одно за другим в какие-то случайные моменты времени. Различают потоки однородных и неоднородных событий.

Однородный ПС характеризуется только моментами поступления этих событий и задаётся последовательностью моментов поступления либо в виде последовательности промежутков времени между n-м и (n-1)-м событиями {t_n}.

Неоднородным ПС называется последовательность {t_n, f_n}, где t_n- вызывающие моменты; f_n- набор признаков события.

 

Однородный ПС с ограниченным последействием, ординарный, с тационарный.

Среднее число событий, наступающих на участке Dt в единицу времени составляет P₁(t, Dt)/Dt. Если существует предел

 

lim P₁(t, Dt)/Dt=l(t)*(1/един.вр.),

 

то он называется интенсивностью (плотностью) ОПС. Для стандартного ПС l(t)=l=const.

Заявки, обслуженные каналом k_i и заявки, покинувшие прибор СМО по различным причинам не обслуженными, образуют выходной поток y_iÎY.

Процесс функционирования СМО можно представить как процесс изменения состояний его элементов во времени Z_i(t).

 

Т.о. для задания Q-схемы необходимо оператор сопряжения R, отражающий взаимосвязь элементов структуры.

 

Различают разомкнутые и замкнутые Q-схемы. В разомкнутой выходной поток не может снова поступить на какой-либо элемент, т.е. обратная связь отсутствует.

 

Собственными (внутренними) параметрами Q-схемы будут являться кол-во фаз L_Ф, количество каналов в каждой фазе, К_j, j=1… К_Ф, количество накопителей каждой фазы L_j, j=1… L_Ф, ёмкость j-ого накопителя L_i^H. В зависимости от ёмкости накопителя применяют следующую терминологию:

- системы с потерями (L^H=0, накопитель отсутствует);

- системы с ожиданием (L^H®¥);

- системы с ограниченной ёмкостью накопителя Н (смешанные).

 

Для задания Q-схемы также необходимо описать алгоритмы её функционирования, которые определяют правила поведения заявок в различных неоднозначных ситуациях.

 

В зависимости от места возникновения таких ситуаций различают алгоритмы (дисциплины) ожидания заявок в накопителе Н_i и обслуживания заявок каналом k_i. Неоднородность потока заявок учитывается с помощью введения класса приоритетов.

 

В зависимости от динамики приоритетов Q-схемы различают статические и динамические. Относительные и абсолютные.

 

Необходимо также знать набор правил, по которым заявки покидают Н_i и k_i:

для Н_i – либо правила переполнения, либо правила ухода, связанные с истечением времени ожидания заявки в Н_i­;

для k_i – правила выбора маршрутов или направлений ухода.

Кроме того, для заявок необходимо задать правила, по которым они остаются в канале k_i, т.е. правила блокировок канала. При этом различают блокировки k_i по выходу и по входу. Такие блокировки отражают наличие управляющих связей в Q‑схеме, регулирующих поток заявок в зависимости от состояний Q‑схемы. Набор возможных алгоритмов поведения заявок в Q‑схеме можно представить в виде некоторого оператора алгоритмов поведения заявок А.

 

Т.о., Q‑схема, описывающая процесс функционирования СМО любой сложности однозначно задаётся в виде набора множеств: Q = <W, U, H, Z, R, A>, где

 

W – поток заявок; U – поток обслуживания; H – правила ухода заявок из накопителя (дисциплины ожидания); Z – состояния (процесс изменения состояний, если во времени); R – связи, задающие структуру схемы; A – алгоритмы (правила поведения заявок в неоднозначных ситуациях).

 

Символика характеристик СМО (5 разрядов)

1-й разряд	2-й разряд	3-й разряд	4-й разряд	5-й разряд
Характеристика входящего потока однородных событий	Характеристика обслуживания	Особенности структуры системы (число приборов)	Особенности очереди	Приоритет

 

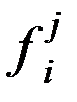
Распределения:

M – экспоненциально распределение (Markovian), E _r – распределение Эрланга порядка r, H _R – гиперэкспоненциальное распределение порядка R,

R – равномерное распределение, D – постоянная величина, G – произвольное распределение (General).

i = 0, 1, 2; J = 0, 1; i = 0 – обслуживание без приоритета;

i = 1 – относительный приоритет; i = 2 – абсолютный приоритет;

j = 0 – требование, заставшее все места занятыми, теряется;

j =1 – вновь прибывшее требование вытеcняет требование с более низким приоритетом.

 

Модели потоков

Под случайным потоком понимается некоторая последовательность событий. наступающих в случайные моменты времени.

В теории сетей передачи данных применяются понятия потоков сообщений, перерывов связи, ошибок в каналах.

Соответствующие события: поступление сообщений, перерывы связи. ошибки в каналах.

Случайный поток может быть задан функцией распределения величины промежутка времени между моментами наступления событий

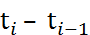= , P ( ≤ t)

Если величины независимы в совокупности, то поток называется с ограниченным последействием.

В случае P ( ≤ t) = P ( ≤ t) для всех i ≥ 2 поток является рекуррентным.

Если P ( ≤ t) = P ( ≤ t) для всех i ≥ 1, то это поток без последействия.

Рекуррентный поток называется пуассоновскис, для которого

P ( ≤ t) = 1 –

Для такого потока вероятность наступления n событий за промежуток времени [0 ,t ]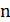

,

а математическое ожидание числа событий, наступивших за время t, есть – среднее число событий, поступающих в единицу времени.

Пуассоновский поток характеризуется отсутствием последействия.

Если, кроме того, соблюдается условие стационарности и ординарности, то пуассоновский поток будет простейшим.

Величина в случае пуассоновского потока называется интенсивностью потока событий.

Если 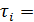= const? то поток является регулярным или детерминированным.

В результате детерминированной операции просеивания образуется поток, который Эрланга, который ближе к егулярному относительно исходного потока (т.е. менее случаен).

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: