 |
Схема расчета замкнутой СеМО
|
|
|
|
Существует два альтернативных метода исследования ЗСеМО - алгоритм свертки, основанный на вычислении нормализующей константы, и метод анализа средних значений [1]. Итерационный метод анализа средних значений характеристик СеМО более прост при определении таких практически важных показателей функционирования, как средние длины очередей и времена ожиданий (пребываний в СеМО), производительности сети и загрузки центров и т.д.
Естественно, в коммутаторе имеется конечное число буферов ОПП для хранения пакетов, следовательно, циркулирует конечное число заданий. Поэтому концептуальная модель коммутатора может быть описана замкнутой СеМО (ЗСеМО), в которой циркулирует конечное число заявок (пакетов) [34].
Узел i такой ЗСеМО представляет собой обслуживающий прибор (возможно многоканальный) с экспоненциальным распределением времени обслуживания и очередь заявок (пакетов), ожидающих обслуживания. Дисциплина обслуживания “первым пришел - первым обслужен” такова, что обслуживающий прибор не простаивает при наличии хотя бы одной заявки в очереди. После обработки пакета в узле i, он с вероятностью Рij (
=1, где N - общее число узлов в ЗСеМО) переходит на обслуживание в другой узел j. Общее число заявок по всей сети постоянно и равно Ј.
Решающим в анализе средних значений является вычисление среднего времени задержки в узле i, i=1,…, N, ЗСеМО. Рассмотрим момент, когда пакет поступает в эту систему Средняя задержка, которую испытывает пакет, состоит из времени 
его обслуживания и времени обслуживания пакетов, ожидавших перед ним в очереди, включая пакет, находившийся на обслуживании [42, 54].
Теорема о входящем потоке для ЗСеМО показательного типа устанавливает, что состояние узла в момент поступления заявки описывается распределением вероятностей, равным распределению для стационарного состояния сети с числом циркулирующих в ней заявок, меньшим на одну [44]. Эта теорема дает возможность измерить среднее число заявок, наблюдаемых в момент поступления. Среднее время задержки (пребывания) заявки в k -ом узле при наличии в сети j заявок связано со средним числом ожидающих при наличии в сети (j-1) заявок соотношением
|
|
|
,
где n k (j), по определению, есть среднее число заявок в узле k при наличии в сети j заявок;
ak - число обслуживающих приборов в k -м узле.
Данное равенство имеет в точности желаемую рекуррентную форму. Применительно ко всей ЗСеМО эта форма выглядит следующим образом.
Обозначим: сеть содержит N узлов;
- вектор средних времен пребывания заявок в СМО сети при наличии в сети v заявок;
обсл k – среднее время обслуживания заявок в k-й СМО,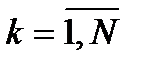 
;
- среднее число заявок в k-й СМО при наличии в сети v заявок;
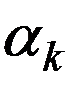- число обслуживающих приборов в k -й СМО;
- среднее время пребывания заявок в Се7МО при наличии в сети v заявок.
Для 
и 
рассчитывается среднее время пребывания в k -й СМО при наличии в сети v заявок.
обсл 
; (4.1)
Среднее время пребывания заявок в замкнутой СеМО при наличии в сети v заявок
(v); (4.2)
; (4.3)
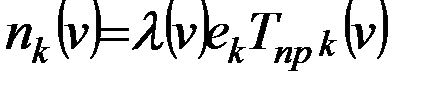; (4.4)
Величина 
- пропускная способность ЗСМО при наличии в ней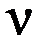 
заявок.
Вектор 
является решением системы линейных уравнений (уравнений баланса для замкнутой сети)
, (4.5)
которая определяет стационарное распределение цепи Маркова, управляющей переходами заявок в ЗСеМО, с матрицей вероятностей переходов
,
где 
=1. Система (4.5) решается при дополнительном ограничении
Выполнение процедуры (4.6) ÷ (4.4) начинается с 
, 
для 
.
Вычисление (увеличение v на 1) ведутся до тех пор, пока ЗСеМО не войдет в состояние насыщения.
Критерий (признак) насыщения:
(4.6)
где 0,9 < 
< 1 – численное значение критерия насыщения [2].
|
|
|
Значение 
, удовлетворяющее (4.6), принимается за пропускную способность (производительность) замкнутой СеМО.
Характер зависимости 
приведен на рис.11.
Таким образом, для аналитического расчета средних значений характеристик коммутатора с общей разделяемой памятью мы будем использовать рекуррентную численную процедуру (4.1) ÷ (4.4) расчета замкнутых сетей массового обслуживания, которая обладает меньшей вычислительной сложностью по сравнению с традиционным вычислением нормировочных констант.
Рис 11. Характеристика процесса насыщения
|
|
|
