 |
Аналитический анализ СМО
|
|
|
|
Экспоненциальная система массового обслуживания
2.2.1.1 Одноканальная однородная экспоненциальная СМО
| K |
| Λ |
|
Рис. 2.3
Приходы заявок образуют пуассоновский поток событий. Это означает, что время между приходами любых двух последовательных заявок есть независимая случайная величина с экспоненциальной функцией распределения вероятностей
F (Х) =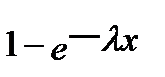 
(2.6)
Одноканальная экспоненциальная СМО задается параметрами λ, . Цель ее анализа заключается в расчете характеристик, важнейшие из которых следующие:
- коэффициент загрузки ρ;
- средняя длина L очереди;
- среднее число М заявок в СМО;
- среднее время 
ожидания обслуживания;
- среднее время 
пребывания заявки в СМО.
Коэффициент загрузки рассчитывается по формуле
ρ = λ · . (2.7)
Если выполняется условие
ρ ≤ 1, (2.8)
то существует стационарный режим функционирования СМО.
В стационарном режиме среднее число М заявок в СМО постоянно. Следовательно, в стационарном режиме интенсивность потока уходящих заявок равна λ. Коэффициент загрузки ρ в стационарном режиме есть:
а) среднее значение той части единицы времени, в течение которой канал занят;
б) вероятность того, что канал занят;
в) среднее число заявок в канале.
Средняя длина очереди (среднее число заявок в очереди) в одноканальной экспоненциальной СМО рассчитывается по формуле
(2.9)
Среднее число М заявок в СМО равно сумме среднего числа L заявок в очереди и среднего числа ρ заявок в канале:
М = 
(2.10)
Заявка перемещается в очереди в среднем с постоянной скоростью. Среднее число переходов заявки в очереди на одно место вперед за единицу времени равно λ.
При такой скорости перемещения L переходов произойдет за время, равное в среднем
|
|
|
= 
(2.11)
Формула (2.11) дает среднее время прохождения заявки через очередь. Это есть среднее время ожидания.
Среднее время пребывания заявки в СМО есть
= 
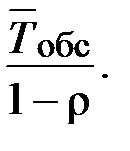(2.12)
Вероятность наличия в системе k требований определяется с помощью геометрического закона распределения в виде
Многоканальная экспоненциальная СМО отличается от одноканальной следующим. Число каналов в ней более одного. Приходящая заявка становится в очередь, если все каналы заняты. В противном случае заявка занимает свободный канал.
Многоканальная экспоненциальная СМО
Многоканальная экспоненциальная СМО задается тремя параметрами: интенсивностью Λ прихода заявок, средним временем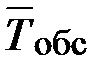 
обслуживания и числом К каналов (рис. 2.4).
| К |
| К |
| λ |
|
Рис. 2.4
Формулы для расчета характеристик многоканальной экспоненциальной СМО немногим сложнее (2.6) - (2.12).
Коэффициент загрузки определяется в виде
Его значение должно отвечать условно стационарности (2.8).
Средняя длина очереди в блоке ожидания
где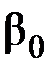 
- стационарная вероятность того, что в СМО нет заявок. Эта вероятность определяется в виде
= 
Остальные характеристики вычисляются через параметры СМО следующим образом:
М = L + K ·ρ; = 
; 
= 
+ 
.
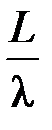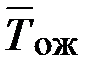Многоканальную СМО можно поставить в соответствие, например, многопроцессорному блоку вычислительной системы, имеющему общую память для всех процессоров и, следовательно, общую очередь задач.
Модель M/G /1
Для однолинейной системы массового обслуживания М / G /1 с пуассоновским потоком на входе, прямой процедурой обслуживания (первым пришел – первым обслужен) и произвольным распределением значений случайного времени обслуживания формула Полячека-Хинчина определяет среднее время ожидания начала обслуживания в виде
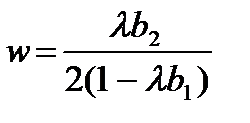, (2.13)
Здесь l – интенсивность входного простейшего потока заявок, 
– среднее время обслуживания, 
– второй момент распределения длительности обслуживания (D – дисперсия).
|
|
|
Заявка перемещается в очереди в среднем с постоянной скоростью. Среднее число переходов заявки в очереди на одно место вперед за единицу времени равно l. При такой скорости переходов за время w заявка совершит Lc переходов. Это есть средняя длина очереди, т.е.
Lc = w l (2.14)
Подставляя в (2.14) вместо w его определение (2.13), получаем выражение для средней очереди СМО М / G /1 в виде
Lc = 
(2.15)
Здесь 
– коэффициент загрузки СМО.
Из (2.15), в частности, следует, что для модели М / М /1 (экспоненциальное время обслуживания), когда D = 
, для средней длины очереди справедливо соотношение
L cэ = 
При фиксированном (постоянном) времени обслуживания D = 0, и
Lcп = 
Для описания пульсирующего потока часто используется распределение Парето с плотностью распределения вероятностей вида
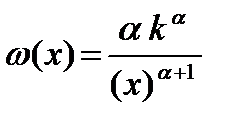; a > 0; х > 0,
где α – параметр формы, k – нижний граничный параметр, т.е. минимальное значение для случайной переменной х. При α > 1 имеет место конечное среднее (м.о.) M(x) = α K /(α – 1), при α > 2 – конечная дисперсия D(x) = M(x 2) – M2(x) = α K 2/(α – 1)2/(α – 2).
Подставляя эти значения в (2.15), получаем выражение для оценки среднего значения очереди при времени обслуживания, оаспределенным по Парето
(2.16)
Сопоставляя (2.16) с (2.15) определяем значение α = (1+ 
). Это значение является пороговым, при превышении которого для экспоненциальной СМО М/М/1 средняя длина очереди оказывается большей, чем для СМО с пуассоновским входным потоком и распределенным по Парето временем обслуживания при одинаковой входящей нагрузке.
|
|
|
