 |
Пример: расчет системы телеобработки данных
|
|
|
|
В качестве примера практического применения аппарата РСеМО рассмотрим задачу, заключающуюся в обоснованном выборе аппаратуры передачи данных (модема) и системного блока центрального вычислительного комплекса из соответствующих унифицированных рядов для комплексирования системы телеобработки заданий.
Задания поступают от отдельных терминалов на концентратор в виде потоков запросов (требований). Будем полагать, что концентратор представляет собой статистический мультиплексор/демультиплексор и обеспечивает суммирование поступающих от терминалов парциальных потоков заданий и распределение ответов с решениями по источникам запросов. Полагаем, что любой источник выдает новый запрос только после получения соответствующего ответа на ранее переданный запрос, т. е. источники имеют единичные емкости. Это позволяет оценивать среднее время задержки на концентраторе по суммарной интенсивности потока запросов, поскольку в силу единичной емкости источников на концентратор поступает либо запрос, либо ответ на него с решением.
Примем также, что запросы и ответы с решениями имеют фиксированный объем и передача запросов и ответов по каналу связи происходит без ошибок. Точнее, их влиянием на конечный результат в рамках поставленной задачи пренебрегаем.
В рамках приведенных ограничений решаем следующую задачу: из унифицированных устройств аппаратуры передачи данных (АПД) (модемов) и системных компьютерных блоков выбрать такие, которые обеспечили бы получение ответа на запрос за время, среднее значение которого не превышало бы заданного значения. Будем также полагать, что естественным ограничением по умолчанию является обеспечение наименьшей стоимости реализации системы.
|
|
|
Итак, имеем следующую постановку задачи.
Задание
Дано:
· структура системы телеобработки данных (СТОД) (рис. 3.1), где Т – терминалы; К – концентратор; АПД (модем) – аппаратура передачи данных; КС – канал связи; ЦВК – центральный вычислительный комплекс;
· суммарный поток требований (запросов), поступающих от терминалов через концентратор на вход АПД, – пуассоновский с интенсивностью 
;
· объем запроса – 
, байт;
· объем результата решения – 
, байт;
· скорость АПД – 
.
Рис. 3.1
Характеристики решаемых задач:
· трудоемкость алгоритма (число машинных операций) – 
, 
;
· число обращений за данными – 
;
· вероятность прохождения k-го алгоритма – 
;
· структура ЦВК (рис. 3.2), где ПР–ОП – процессор–оперативная память (системный блок); ВЗУ – внешнее запоминающее устройство. ВЗУ1 хранит данные; ВЗУ2 хранит программы задач;
· интенсивность обслуживания: на ВЗУ1 – 
, на ВЗУ2 – 
, 1/c;
· быстродействие процессора – 
, операций/с;
· допустимое время получения ответа – 
.
Рис. 3.2
Требуется: выбрать процессор из ряда , и АПД из ряда , так, чтобы среднее время получения ответа с решением 
удовлетворяло условию 
.
Решение
Время получения ответа складывается из времени задержки задания/ответа с решением на концентраторе 
, времен передачи задания 
и ответа 
и времени 
, затрачиваемого на решение задания на ЦВК:
,
где j – номинал скорости передачи АПД, двоичных знаков/с; i – номинал быстродействия ПР–ОП, операций/с.
Поскольку АПД обеспечивает дуплексный канал,
; 
.
Для оценивания значений и требуется формализовать процесс решения.
Задержка на концентраторе может возникнуть из-за ожидания передачи задания либо ответа с решением источнику по причине занятости канала передачи данных. Формализуем работу концентратора экспоненциальной одноканальной однородной СМО (см. рис. 1.2). Среднее время обслуживания для такой СМО определяется средним временем занятости АПД, которое определим в виде
|
|
|
,
и среднее время задержки на концентраторе определим как среднее время ожидания в очереди, согласно (1.2):
. (3.1)
Отметим, что при расчете нужно следить за тем, чтобы выполнялось соотношение 
, поскольку мы рассматриваем стационарную СМО.
Для формализации расчета ЦВК используем схему разомкнутой сети массового обслуживания (рис. 3.3), где S1 отображает ПР–ОП; S2 отображает ВЗУ1; S3 отображает ВЗУ2.
Рис. 3.3
СеМО, изображенная на рис. 3.3, задается следующими параметрами:
1) числом N СМО – N = 3;
2) числом каналов обслуживания в каждой СМО 
;
3) матрицей 
вероятностей передачи 
, 0 – внешняя среда;
4) интенсивностями 
входных потоков – здесь 
;
5) средними временами обслуживания 
заявок в СМО – здесь 
(
– время обслуживания отдельного требования на процессоре, зависит от значения производительности 
),
.
Среднее время пребывания заявки в СеМО рассчитывается по формуле 
,
где 
; здесь 
, 
– время пребывания заявки
в j-й СМО, j = 1, 2, 3.
Необходимо найти интенсивности 
, 
, 
и 
, 
, 
.
Рассмотрим алгоритм расчета среднего времени пребывания заявки в ЦВК:
1. Интенсивности , , определяются на основе уравнений баланса сети с учетом свойств слияния и разветвления потоков. Слияние и разветвление задаются матрицей переходов Р. В нашем случае, согласно рис. 3.3,
.
1.1. Система уравнений баланса. Для сети без потерь 
, 
:
(3.2)
1.2. Решение системы (3.2):
(3.3)
где 
– передаточные коэффициенты. Заявка входит в сеть. Ее маршрут в сети случаен, поэтому случайно и число проходов заявки через j-ю СМО. Среднее число проходов называется передаточным коэффициентом.
1.3. Усредним число обращений за данными по всем задачам (запросам). Среднее число обращений к данным на ВЗУ1
. (3.4)
Как видно из рис. 3.4, в процессе решения задача как бы «проходит» через ПР–ОП 
раз: 1 раз идентифицируется и обращается к ВЗУ2 (за программой), 
раз прерывается для обращения за данными к ВЗУ1 и 1 раз обработка задания завершается и готовое решение выходит из СМО S1 во внешнюю среду.
Рис. 3.4
1.4. Следовательно, переходные вероятности можно теперь определить в виде
; 
; 
. (3.5)
1.1. Согласно (3.3) и (3.5), имеем выражения для передаточных коэффициентов: 
, 
, 
.
|
|
|
1.2. И соответственно,
; 
; 
. (3.6)
Теперь можно записать:
. (3.7)
2. Определение 
(время пребывания заявки в СМО).
2.1. Для экспоненциальной СМО
, (3.8)
где m – интенсивность обслуживания заявки.
2.2. Здесь 
– коэффициент загрузки,
. (3.9)
2.3. Определим время обслуживания отдельного запроса на ПР–ОП (S1):
2.3.1. Средняя трудоемкость решения задачи
. (3.10)
2.3.2. Трудоемкость обслуживания отдельного обращения
. (3.11)
2.3.3. Время обслуживания отдельного обращения при быстродействии процессора 
,
. (3.12)
2.4. Интенсивности обслуживания 
и 
заданы на ВЗУ1 и ВЗУ2 соответственно, тогда
; (3.13)
; (3.14)
. (3.15)
2.5. Времена пребывания отдельного обращения (требования) в соответствующих СМО
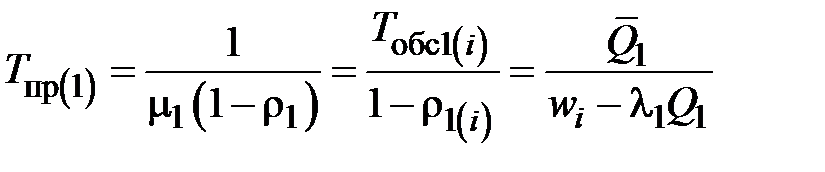; (3.16)
(3.17)
(3.18)
Таким образом, определены передаточные коэффициенты 
, и времена пребывания отдельных требований 
, 
, 
в соответствующих СМО. Подставим выражения для нахождения этих величин в (3.7) и определим 
.
3. Время решения задачи на ЦВК
. (3.19)
4. Итак, составляющие времени ответа с решением определены. Напомним, что общее среднее время ответа складывается из времен передачи запроса и решения, времени задержки на концентраторе (3.1) и времени получения решения на ЦВК (3.19):
. (3.20)
Это общее время получения ответа на запрос должно удовлетворять условию
(3.21)
и задавать допустимый вариант комплексирования АПД и ЦВК.
Приведем основные шаги последовательности расчета среднего времени пребывания заявки в ЦВК:
Преамбула: формализация системы ЦВК в виде РСеМО.
1. Нахождение интенсивностей входных потоков отдельных СМО: 
, 
, 
:
1.1. Построение системы уравнений баланса (3.2).
1.2. Решение системы уравнений баланса (3.3).
1.3. Усреднение числа обращений за данными на ВЗУ1 (3.4).
14. Вычисление переходных вероятностей (3.5).
1.1. Определение значений передаточных коэффициентов.
1.2. Определение интенсивностей входных потоков отдельных СМО (3.6).
2. Определение времени пребывания требований в СМО S1, S2, S3:
2.1. Нахождение времени пребывания заявки в системе отдельной СМО (3.8).
2.2. Определение коэффициента загрузки (3.9).
|
|
|
2.3. Определение времени обслуживания отдельного запроса:
2.3.1. Определение средней трудоемкости решения задачи (3.10).
2.3.2. Определение средней трудоемкости обслуживания отдельного обращения (3.11).
2.3.3. Определение времени обслуживания отдельного запроса (3.12).
2.3.4. Определение коэффициентов загрузки S1, S2, S3 (3.13)–(3.15).
2.3.5. Определение времени пребывания отдельного обращения (требования) в соответствующей СМО (3.16)–(3.18).
3. Вычисление среднего времени, затрачиваемого на получение решения в ЦВК по запросу (3.19).
4. Выражение для вычисления общего времени ответа на запрос (3.20).
5. Условие для комплексирования вариантов АПД и процессоров в систему (3.21).
Отметим довольно универсальный характер рассмотренной схемы расчета. Концептуально к схеме СТОД (см. рис. 3.1) можно свести топологию локальной сети (ЛС) технологии «клиент – сервер»: терминалы – рабочие станции ЛС, канал ПД (АПД + КС) – моноканал ЛС (общая среда передачи), ЦВК – сервер. Величину
можно рассматривать как оценку производительности локальной сети.
|
|
|
