 |
Вычисление пройденного пути
|
|
|
|
Найдем общую формулу для вычисления пройденного частицей пути S в промежутке времени от 
до 
, если известна зависимость модуля вектора скорости от времени 
.
Допустим, что зависимость представлена графиком, показанным на рисунке 1.4. Разобьем мысленно проме-жуток времени – на N столь небольших отрезков 
, чтобы можно было считать скорость 
на отрезке неизменной. Тогда путь 
за каждый интервал находится по формуле 
, а весь путь:
.м м (1.15)
C геометрической точки зрения каждое из слагаемых в соотношении (1.15) представляет собой площадь прямоугольника высотой 
и основанием 
. Сумма (1.15) дает приблизительную площадь фигуры, ограниченной осью времени, графиком и прямыми t = и t = . Точное значение пути получится, если положить, что 
, а 
:
. (1.16)
Выражение (1.16) представляет собой определенный интеграл от в пределах от до :
(1.17)
При этом геометрически пройденный путь изображается площадью, ограниченной графифком , осью времени и вертикальными отрезками, изображающими значения скорости в начальный и конечный момент.
Если в соотношение (1.17) вместо подставить вектор 
, то, поскольку в соответствии с определением 
есть перемещение за 
, интеграл
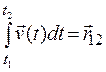(1.18)
даст перемещение частицы за – .
СРЕДНИЕ ЗНАЧЕНИЯ
Традиционно (в быту) средней скоростью называют среднее значение модуля вектора скорости, которое, по определению, равно отношеню всего пути S, пройденного телом за некоторый промежуток времени – , к величине этого промежутка:
. (1.19)
Эту величину называют также средней путевой скоростью.
Соотношение (1.19) есть результат применения общей формулы для нахождения среднего значения скалярной или векторной функции 
на промежутке изменеия аргумениа от 
до 
:
|
|
|
. (1.20)
В частном случае, подставив в (1.20) в качестве вектор скорости, получим для среднего значения вектора скорости:
. (1.21)
Не следует путать понятие средней скорости частицы (1.19) со средним значением скорости для совокупности одинаковых объектов, например среденй скорости молекул, средней скорости автомобилей данного таксопарка в некоторый момент времени и т.п.
Ускорение
Ускорением называют векторную величину, характеризующую быстроту изменения вектора скорости, и количественно определяемую соотношением
(1.22)
Поскольку скорость 
(1.6), то, по аналогии двумя составляющими вектора скорости, характеризующими изменение радиус-вектора частицы, логично выделить две составляющих ускорения:
. (1.23)
Направление составляющей 
совпадает с 
, т.е с касательной к траектории движения и скоростью, поэтому ее называют тангенциальным ускорением. Эта составляющая ускорения определяет быстроту изменения вектора скорости по модулю.
Составляющая 
направлена перпендикулярно скорости (
– производная орта) и называется нормальным ускорением. 
характеризует быстроту изменения скорости по направлению.
Обсудим более подробно чем определяется нормальное ускорение. Легко понять, что быстрота изменения направления вектора скорости, а значит и нормального ускорения, будет тем больше, чем сильнее искривлена траектория и чем больше модуль скорости перемещения частицы по траектории. Для количественной характеристики степени скривленности траектории используется величина, называемая кривизной траектории:если при перемещении вдоль траектории на расстояние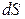 
(см.рис.1.5) касательная к траектории (а значит и вектор скорости) поворачивается на угол 
, то кривизной траектории в данной ее точке называется:
. (1.24)
Величина R, обратная кривизне,
Гласно формуле (1.3)
(1.26)
.
где 
- орт нормали к траектории, направленный в сторону поворота касательной к траектории 
.
|
|
|
Путь который проходит частица за время с одной строны из геометрических соображений можно найти как
. (1.27)
С другой стороны – 
. (1.28)
Приравнивая правые части этих соотношений, находим:
. (1.29)
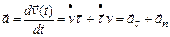
Тогда в соответствии с (1.23) Для
для нормального ускорения получаем:
. (1.30)
Полное ускорение
. (1.31)
|
|
|
