 |
Схема энергетических уровней атома водорода.
|
|
|
|
 |
Действие правила отбора (35.6) приводит к тому, что не все переходы между энергетическими уровнями действительно могут реализоваться. Например переход из состояния 2 s в 1 s не может произойти, поскольку противоречит правилу отбора. В связи с этим схему энергетических уровней электрона в атоме водорода можно представлять так, как это показано на рисунке 35.1
Состояние 1s является основным состоянием атома водорода, в котором атом водорода обладает минимальной энергией. Фотон при поглощении его атомом исчезает полностью, передавая атому свою энергию, поскольку является неделимым. Поглощающий атом обычно находится в основном состоянии, поэтому спектр поглощения водородного атома должен состоять из линий, соответствующим переходам 1 s-np, что полностью соответствует результатам экспериментов.
Электрон в атоме водорода
Собственные функции уравнения Шрёдингера для атома водорода распадаются на два множителя, один из которых зависит только от r, а другой от углов J и j.
(35.7)
Множитель 
вещественный, 
- мнимый. Функция является собственной функцией оператора квадрата момента импульса. Для s -состояний электрона (т.е. с моментом импульса равным нулю) эта функция является константой, и 
-функции вида 
зависят только от r.
Элемент объема dV сферической системе координат можно представить в виде
где d W = 
есть элемент телесного угла.
Вероятность dP 
нахождения электрона в элементе dV
(35.8)
Взяв интеграл от (35.7) по телесному углу 4 p, найдем вероятность 
нахождения электрона в тонком шаровом слое радиуса r и толщины dr:.
(35.9)
Поскольку Y 
предполагаются нормированными, интеграл в (35.9) равен единице, и
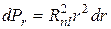(35.10)
Из (35.9) вытекает, что 
есть плотность вероятности нахождения электрона на расстоянии r от ядра,
|
|
|
Длинными вертикальными черточками показаны радиусы соответствующих боровских орбит.
Рисунок 35.1
Спектры щелочных металлов
Эти спектры похожи на спектр испускания атома водорода, но только качественно. Наблюдается несколько серий линий и наиболее интенсивные из них получили названия на основе наблюдаемых экспериментально особенностей:
резкая (sharp) – линии этой серии выглядели очень четкими и узкими.
главная (principal) – линии этой серии наблюдались и в спектрах поглощения и спектрах испускания, что указывало, что они соответствуют переходу атомав в основное состояние;
размытая (diffuse) – линии этой серии выглядели размытыми, нечеткими;
основная (fundamental) – линии этой серии напоминали серии линий атома водорода.
Установлено, что рассмотренные серии линий связаны с переходами внешнего (валентного) или оптического электрона.
Система энергетических уровней, соответствующих испусканию указанных линий для атома натрия имеет вид, приблизительно показанный на рисунке 35.3.
В отличие от атома водорода, энергия состояния оказывается зависящей не только от значения квантового числа n, но и от номера ряда термов. Ряды термов, как и в атоме водорода соответствуют различным значениям азимутального квантового числа l.
Эти выводы соответствуют результатам квантовомеханических расчетов – решению уравнения Шредингера для электрона, движущегося в центрально-симметричномнекулоновском поле. Поле ядра в атомах щелочных металлов частично экранируется электронами внутренних электронных оболочек атомов. При этом поле сохраняет сферическую симметрию, но от от расстояния до ядра изменяется по закону, отличному от закона Кулона. В таком поле энергия электрона оказывается зависящей от квантового числа: 
Об этом принято говорить, что снимается вырождение по азимутальному квантовому числа 
. Однако, в основном энергия зависит все же от главного квантового числа n.
|
|
|
Установлено, что момент импульса атомного остатка щелочных атомов после удаления оптического электрона равен нулю. Следовательно, азимутальное квантовое число L результирующего момента импульса атома совпадает с азимутальным квантовым числом валентного электрона. При возбуждении атома (т.е. при переводе некоторым воздействием из состояния с минимальной энергией в состояние с большей энергией) и при испускании им света изменяется состояние только валентного электрона, поэтому схема уровней атома тождественна схеме уравнения валентного электрона.
Термы, отвечающие столбцам уровней, на схеме энергетических уровней можно обозначить символами nS, nP, nD и nF. Тогда частоты спектральных линий, равные разности термов конечного и начального состояний можно представить в следующем виде:
резкая 
,
главная 
,
диффузная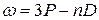 
,
основная 
.
Ридберг установил, термы щелочных металлов можно представить в виде:
(35.11)
где 
- ридберговская поправка (имеется ввиду поправка в сравнении с термами атома водорода).
Эта поправка одинакова для всех термов данного ряда (с данным азимутальным квантовым числом) и обозначается буквой соответствующей ряду.
Соответственно для резкой серии можно записать:
Следуя этому правилу частоты линий серий атома натрия можно представить в виде:
резкая 
главная 
диффузная 
основная 
Ширина спектральных линий
До сих пор, говоря о спектральных линиях и энергетических уровнях, мы имели в виду строго определенные конкретные величины. В действительности это не совсем так.
Из возбужденного состояния атом может спонтанно перейти в более низкое энергетическое состояние. Время t, за которое число атомов в данном возбужденном состоянии уменьшается в e раз, называется временем жизни возбужденного состояния. По порядку величины эта величина время жизни возбужденного состояния составляет 
Возможность спонтанных переходов указывает на то, что возбужденные состояния нельзя считать строго стационарными. В силу того, что время и энергия являются канонически сопряженными величинами, соотношение неопределенностей определяет конечную ширину Г энергетических уровней:
|
|
|
Только основное состояние не допускает спонтанных переходов и его энергия имеет строго определенное значение.
В соответствии с конечным Г, интервал частот излучаемых фотонов 
Для видимого света с 
соответствующее 
Это так называемая естественная ширина спектральной линии.
Тепловое движение атомов приводит к доплеровскому расширению спектральных линий. При этом для излучения с длиной волны 
при температуре Т = 1000 К получается значение 
, которое во много раз превосходит естественную ширину спектральных линий.
|
|
|
