 |
Результирующий механический момент многоэлектронного атома
|
|
|
|
При образовании в результате сложения спиновых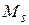 
и орбитальных 
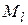моментов импульса электронов результирующего момента атома 
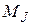возможны два случая:
1. магнитное взаимодействие орбитальных моментов 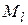различных электронов сильнее, чем их взаимодействие со спиновыми моментами 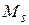. Аналогично спиновые моменты связаны между собою сильнее, чем с орбитальными. В результате сначала образуются результирующие орбитальный 
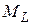и спиновой 
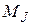моменты импульса, которые затем складываются между собой и образуют . Такая связь называется LS-связью или Рёссель-Саундерсовской и встречается наиболее часто.
2. У ряда тяжелых атомов 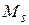и 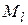каждого электрона взаимодействуют между собой сильнее, чем с моментами других электронов. Поэтому сначала образуются результирующие 
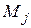отдельных электронов, а потом 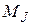всего атома. Это случай j j-связи.
В случае LS -связи, поскольку орбитальные квантовые числа отдельных электронов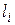 
всегда целые, квантовое число L результирующего орбитального момента также всегда целое.
Квантовое число S результирующего спинового момента атома может быть целым или полуцелым в зависимости от числа электронов в атоме: четное-нечетное.
При данных L и S квантовое число результирующего момента J может иметь значения
J = L + S, L+S- 1 ,…| L- S|,. (36.10)
т.е. может быть и целым и полуцелым.
Энергия атома зависит от взаимной ориентации орбитальных моментов отдельных электронов 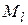- квантового числа L, взаимной ориентации спиновых моментов электронов - квантового числа S и взаимной ориентации результирующих моментов квантового числа J.
Термы многоэлектронных атомов обозначают аналогично термам щелочных металлов символами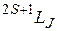 
. Такое обозначение удобно тем, что содержит в себе сведения о значениях трех квантовых чисел: S, L, J. Если S < L, стоящее слева вверху число 2 S + 1 дает мультиплетность терма, как и в случае щелочных металлов. Если S > L, то фактическая мультиплетность равна 2 L + 1, однако символ терма не изменяют, чтобы была возможность указать значение квантового числа S.
|
|
|
Магнитный момент атома
Напомним, что с механическим моментом импульса атома M обязательно связан магнитный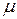 
, а их отношение называется гиромагнитным отношением: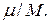 
Для орбитальных моментов экспериментальное значение гиромагнитного отношения
,
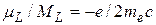т.е. совпадает с классическим значением.
Поэтому орбитальный момент многоэлектронного атома определяется соотношением:
(36.11) 
При этом проекция орбитального момента
. (36.12)
Для спиновых моментов гиромагнитное отношение в 2 раза больше (удвоенный магнетизм спина):
. (36.13)
Поэтому гиромагнитное отношение для результирующих моментов зависит не только от квантового числа J результирующего момента импульса, но и от квантовых чисел L и S. Как показывают расчеты,
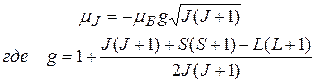. (36.14)
называется фактор или множитель Ланде.
При этом проекция результирующего магнитного момента может принимать значения, определяемые соотношением:
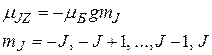. (36.15)
Эффект Зеемана
Эффектом Зеемана называют расщепление энергетических уровней атомов под действием магнитного поля.
Атом, обладающий магнитным моментом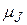 
, приобретает в магнитном поле дополнительную энергию.
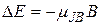. (36.16)
где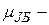 
проекция магнитного момента на направление 
.
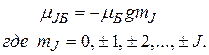. (36.17)
Вследствие этого, энергетический уровень, отвечающий терму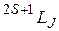 
расщепляется на 2 J + 1 равностоящих подуровней, причем величина расщепления зависит от g, L, S, J.
Можно сказать, что магнитное поле снимает вырождение по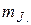 
Рассмотрим Зеемановское расщепление для линий, не имеющих тонкой структуры, т.е. для линий, возникающих при переходах между уровнями, отвечающими S = 0 (для таких уровней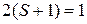 
).
|
|
|
При S = 0 фактор Ланде g = 1,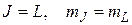 
и
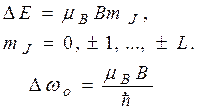. (36.18)
Смещение компонент на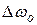 
называется нормальным смещением.
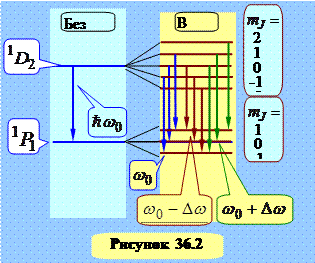
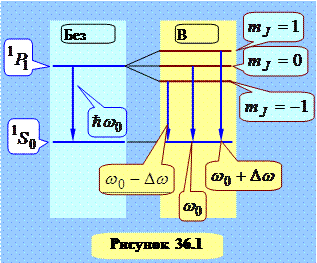
Расщепление линии на 3 линии, сдвинутые на 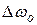, как это показано на рисунке 36.1, называется простым (нормальным) эффектом Зеемана. В более сложном случае, показанном на рисунке 36.2 в магнитном поле расщепляются оба уровня. Но для квантового числа 
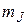имеется правило отбора: возможны только такие переходы, при которых:
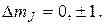(36.19)
Это приводит к тому, что в эксперименте и в этом случае будут наблюдаться три линии, смещенные на .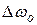
У линий, обладающих тонкой структурой, число компонент более трех, а величина расщепления
r, q – небольшие целые числа.
Такое расщепление называется сложным или аномальным эффектом Зеемана.
|
|
|
