 |
Тонкая структура спектров щелочных металлов
|
|
|
|
Спин электрона
Исследование спектров щелочных металлов показало, что каждая из линий является двойной (говорят образует дублет). Структура спектра, отражающая расщепление линий на компоненты, называется тонкой структурой.
Сложные линии, состоящие из нескольких компонент, называют мультиплетами.
Расщепление спектральных линий очевидно связано с расщеплением энергетических уровней. Для объяснения этого расщепления Гаудсмит и Уленбек в 1925 г. предположили, что электрон обладает собственным моментом импульса, не связанным с движением в пространстве и называемым спином. Наличие у электронов спина следует считать вполне достоверно установленным и рассматривать спин, как внутреннее свойство, присущее электрону так же как заряд и масса.
Величина (модуль) спина электрона определяется по общим законам квантовой механики, так называемым спиновым квантовым числом s, равным ½:
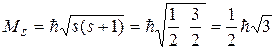(36.1)
Проекция спина на заданное направление может принимать квантованные значения, отличающиеся на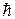 
:
. (36.2)
Спиновое магнитное квантовое число 
может принимать значения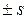 
.
Экспериментально было установлено, что гиромагнитное отношение (отношение магнитного момента к связанному механическому) для спинового момента
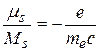. (36.3)
В сравнением с гиромагнитным отношением для орбитального движения электрона значение (36.3) в два раза больше. Об этом принято говорить, что спин обладает удвоенным магнетизмом. Спиновой магнитный момент, как следует из формулы (36.3):
. (36.4)
Знак «-» указывает на противоположность направлений магнитного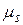 
и механического 
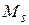моментов. Напомним, что магнетон Бора 
Соответственно проекция спинового магнитного момента может принимать значения
|
|
|
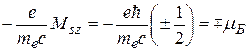. (36.5)
Термы щелочных металлов
Во многие формулы, в частности для энергии, входят не сами магнитные моменты, а их проекции. Поэтому обычно говорят, что спин электрона равен половине (в единицах 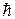), а спиновой магнитный момент – магнетону Бора.
Момент импульса электрона в атоме натрия (равный моменту всего атома) слагается из спинового и орбитального. По квантовым правилам сложения величина суммарного момента определяется квантовым числом 
результирующего момента импульса электрона
. (36.6)
С механическими моментами связаны магнитные, которые могут взаимодействовать. Грубо взаимодействие спинового и орбитального магнитных моментов можно представлять себе как взаимодействие двух магнитных стрелок. Вполне очевидно, что энергия взаимодействия спинового и орбитального магнитных моментов (спин-орбитального взаимодействия) зависит от их взаимной ориентации, которая на квантовом языке описывается квантовым числом . Следовательно, состояния с различными числами j должны обладать различной энергией, а у энергетических уровней и спектров, возникающих при переходах между такими уровнями, появляется тонкая структура.
В соответствии с двумя возможными по формуле (36.6) значениями j, каждый терм ряда р, для которого l = 1, распадается на два, отвечающих 
и 
. Точно также каждый терм ряда d (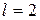
) расщепляется на два с и 
. Не расщепляются термы ряда s, (
), поскольку имеют только одно значение квантового числа результирующего момента импульса .
Термы атомов щелочных металлов можно обозначить символами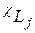 
, в которых буква (
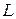) указывает на значение азимутального квантового числа (
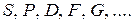) для данного ряда термов, верхний индекс – мультиплетность терма (т.е. количество компонент), а нижний правый индекс – значение квантового числа результирующего момента импульса валентного электрона. Поэтому дублетные термы атомов щелочных металлов можно обозначить следующим образом:
|
|
|
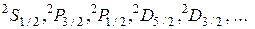
При переходах атомов между различными состояниями на изменения квантового числа результирующего момента импульса j накладывается правило отбора:
. (36.8)
Релятивистская квантовая теория дает для расстояния между подуровнями тонкой структуры водородного атома значение
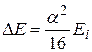. (36.9)
где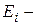 
энергия ионизации атома водорода;
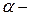постоянная тонкой структуры: 
Постоянная тонкой структуры характеризует энергию взаимодействия двух электронов, выражается через и принадлежит к числу фундаментальных констант природы.
|
|
|
