Собственная проводимость полупроводников.

Напомним, что полупроводники – это кристаллы, которые при низких температурах имеют полностью заполненную валентную зону. (Название зоны отражает тот факт, что в модели сильно связанных полупроводников эта зона возникает при расщеплении энергетического уровня, на котором в отдельных атомах находились валентные электроны.) Поэтому при низких температурах полупроводники являются изоляторами. В отличие от классических диэлектриков у полупроводников полностью заполненная валентная зона отделена от следующей зоны разрешенных значений энергии запрещенной зоной шириной порядка одного электрон-вольта. В диэлектриках этот параметр составляет порядка 3 эВ. Не очень большая ширина запрещенной зоны обеспечивает возможность осуществления в полупроводниках явления, отличающего их от классических диэлектриков: с ростом температуры и возрастанием интенсивности теплового движения становится возможным получение отдельным электроном энергии, достаточной для перехода в зону разрешенных энергий. (Принципиально этот процесс возможен и в диэлектриках, однако температуры необходимые для этого столь высоки, что не совместимы с существованием кристалла.)

Попав в свободную зону, электроны не могут сразу вернуться в валентную зону, поскольку в окружающем пространстве состояния с соответствующей энергией заняты. Если к кристаллу приложить внешнее электрическое поле, электроны будут получать от него энергию, ускоряться в направлении против вектора его напряженности и переносить заряд, т.е. создавать электрический ток. Поэтому в полупроводниках (!) свободную зону разрешенных значений энергии, ближайшую к валентной называют зоной проводимости.

При переходе электрона в зону проводимости в валентной зоне освобождаются энергетические уровни вблизи ее потолка. Электроны валентной зоны получают возможность ускоряться в электрическом поле, увеличивая свою энергию и занимая освободившиеся уровни. Однако эффективная масса электронов вблизи потолка валентной зоны отрицательна, и движение таких электронов удобнее рассматривать как движение дырок. Причем количество дырок в валентной зоне совпадает с количеством электронов в зоне проводимости. Проводимость полупроводника в условиях, когда носители заряда образуются только за счет термических забросов электронов валентной зоны в зону проводимости, называется собственной. Такой проводимостью обладают химически чистые полупроводники. Процесс возникновения свободного электрона в зоне проводимости и дырки в валентной называют генерацией электронно-дырочной пары.

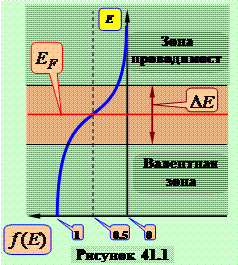Распределение электронов по уровням, описывается функций распределения: . График этой функции при температурах, когда собственная проводимость стала существенной приблизительно показан на рисунке 41.1.

Расчеты показывают, что если отчитывать от потолка валентной зоны, то положение уровня Ферми в собственном полупроводнике описывается выражением:

(41.4)

где и - эффективные массы электронов и дырок,

- ширина запрещенной зоны.

Обычно эффективные массы электронов и дырок отличаются незначительно, и вторым слагаемым в (41.4) можно пренебречь по сравнению с . Поэтому с высокой точностью можно утверждать, что в собственных полупроводниках уровень Ферми находится в середине запрещенной зоны:

. (41.5)

Для электронов в зоне проводимости справедливо соотношение:

и, 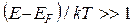. (41.6)

В этом случае вместо распределения Ферми-Дирака можно использовать распределение Больцмана, в соответствии с которым вероятность заполнения энергетического уровня с энергией равна:

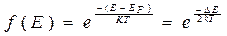. (41.7)

Количество электронов в зоне проводимости, а значит и их концентрация, пропорционально этой вероятности. Поскольку проводимость 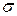, в свою очередь, пропорциональна концентрации электронов, то температурная зависимость проводимости описывается выражением:

. (41.8)

Логарифмируя это выражение, получаем:

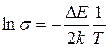. (41.8)

 

Таким образом, температурная зависимость электропроводности полупроводника с собственной проводимостью в координатах должна иметь вид прямой линии, наклон которой определяется шириной запрещенной зоны, как это показано на рисунке 41.2. Экспериментальные исследования подтвердили справедливость выводов зонной теории электропроводности.

Очень часто при рассмотрении проводимости полупроводников полезными оказываются модельные представления. Для типичных полупроводников и кристаллическую структуру можно представить на плоскости в виде, показанном на рисунке 41.3. Каждый атом обладает четырьмя валентными электронами, которые образуют связи с четырьмя ближайшими атомами. При достаточно высокой температуре происходит разрыв некоторых связей. Освободившийся электрон оказывается в межузельном пространстве и может участвовать в создании электрического тока, а в окрестности разорванной связи появляется нескомпенсированный положительный заряд. Валентные электроны данного атома могут восстановить связь в месте ее разрыва, однако при этом разорванная связь сместится в другое место. Если разорванная связь за счет перехода электронов от других атомов будет перемещаться по кристаллу, то вместе с ней будет перемещаться и положительный заряд, который можно считать моделью дырки.

При достаточно высокой концентрации свободных электронов и дырок может происходить захват свободного электрона атомом для заполнения разорванной связи. При этом исчезают электрон и дырка. Такой процесс называется рекомбинацией электронно-дырочной пары. В представлениях зонной теории рекомбинации соответствует переход электрона из зоны проводимости в валентную, сопровождающийся выделением энергии, которая может быть унесена фотоном или передана кристаллической решетке.

Примесная проводимость

Примесная проводимость возникает в том случае, когда в полупроводник (например, Ge) вводятся атомы, у которых количество валентных электронов отличается на единицу (например, As). Атомы As в кристалле Ge замещают атомы основного вещества, т.е. располагаются не в промежутках между атомами Ge, а в место них. При этом из пяти валентных электронов As четыре задействуются для образования связей с соседними атомами Ge. Пятый (при низких температурах, когда энергия теплового движения мала) связан с атомом примеси и образует с ним систему, напоминающую атом водорода. Поэтому модель легированного такой примесью полупроводника можно представлять в виде идеального кристалла, в котором хаотическираспределены притягивающие центры с зарядами + е и такое же число электронов, которые могут быть связанны с этими центрами.

Если бы примесь находилась в вакууме, то энергия связи электронов с положительными центрами равнялась бы просто энергии ионизации, равной для мышьяка 9,81 эВ. Однако, благодаря тому, что примесь находится в полупроводнике, энергия связи электрона очень сильно уменьшается. Это происходит по следующим причинам. Движение электрона в поле заряда, примесного атома, происходит в кристалле, и напряженность электрического поля уменьшается в e раз (e - диэлектрическая проницаемость полупроводника). Обычные значения e полупроводников заключены в интервале от 10 до 20, но могут быть и значительно большими у полупроводников с малой запрещенной зоной. Электрон, движущийся под действием электрического поля в кристаллической решетке, характеризуется эффективной массой , (учитывающей влияние периодического поля кристаллической решетки) которая меньше массы свободного электрона во многих случаях в 10 и более раз. Поэтому радиус первой боровской орбиты (а_о= 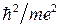)) оказывается равным и может достигать 10^–8 м и более, т.е. большого количества межатомных расстояний. Энергия связи в основном состоянии ( для атома водорода) в рассматриваемой система описывается выражением Е _св= 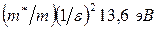, т.е. уменьшается в тысячу и более раз и оказывается не просто малой, а малой по сравнению с шириной запрещенной зоны (узкая зона - большая e).

Таким образом, атомы примеси образуют дополнительные электронные уровни в запрещенной зоне вблизи дна зоны проводимости, соответствующего свободным электронам. Причем энергетический зазор 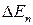между дополнительными уровнями и дном зоны проводимости намного меньше ширины запрещенной зоны полупроводника. Примерный вид энергетической диаграммы рассматриваемого легированного полупроводника при температуре вблизи абсолютного нуля показан на рисунке 1.

При повышении температуры связанные электроны на примесном уровне получают энергию, достаточную для перехода на свободные уровни зоны проводимости, т.е. разрывают связь с атомом примеси, становятся свободными и могут осуществлять перенос заряда в полупроводнике, создавая электрический ток. Примесные атомы становятся положительно заряженными ионами, суммарный заряд которых равен заряду ставших свободными электронов, и полупроводник в целом остается электрически нейтральным.

Атомы примеси, отдающие электроны в зону проводимости называют донорами, а полупроводник донорным или n-типа (в соответствии со знаком свободных носителей заряда). Уровень Ферми , расположенный в собственном (нелегированном) полупроводнике в середине запрещенной зоны, в примесном полупроводнике располагается вблизи примесного уровня.

Введение в полупроводник атомов примеси с количеством валентных электронов на единицу меньше отражается на энергетической диаграмме полупроводника похожим образом – рис. 2. Вблизи потолка валентной зоны появляется примесный уровень, к которому смещается уровень Ферми . При абсолютном нуле атомы примеси нейтральны, но для образования ковалентных связей с окружающими атомами основного вещества им не хватает по одному электрону. С повышением температуры электроны валентной зоны получают возможность перейти на свободные примесные уровни, оставляя в валентной зоне свободные уровни. Во внешнем электрическом поле электроны валентной зоны получают возможность переходить на освободившиеся уровни, т.е. получать энергию от электрического поля и участвовать в создании электрического тока. Движение электронов с энергиями вблизи потолка валентной зоны эквивалентно движению положительно заряженных частиц, которые называют дырками. Поэтому легирование в данном случае приводит к появлению в валентной зоне значительного количества свободных дырок.

Электроны, перешедшие на примесный уровень, участвуют в образовании ковалентных связей и перемещаться по кристаллу не могут. В окрестности примесного атома, захватившего электрон валентной зоны, образуется избыточный отрицательный заряд. Атомы примеси в этом случае называют акцепторами, а легированный ими полупроводник акцепторным или р-типа (по знаку положительных носителей заряда).

Концентрация свободных носителей заряда в примесных полупроводниках складывается из концентрации 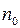, обусловленной переходами в зону проводимости электронов валентной зоны, и , обусловленной легированием полупроводника:

. (1)

Температурная зависимость этих концентраций в соответствии с распределением Больцмана, описывается соотношениями:

и (2)

Поскольку << , то в широкой области температур от нескольких кельвинов до температур, соответствующих kT, сравнимому с , в примесном полупроводнике концентрация носителей одного знака значительно превышает концентрацию носителей другого знака. Носители тока с большей концентрацией называются основными: электроны в донорном полупроводнике, дырки – в акцепторном.

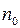При температурах соответствующих kT порядка , концентрация начинает преобладать над , и примесная проводимость становится пренебрежимой в сравнении с собственной.

P – n переход.

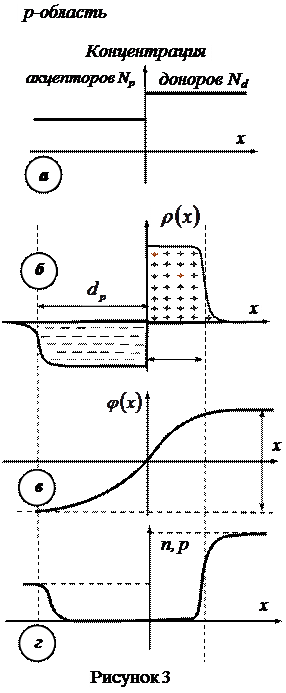
Большинство технических применений полупроводников основано на ис­пользовании свойств кристаллов, в которых специально создается неоднород­ное распределение концентраций донорных и акцепторных примесей. Про­стейшим примером структуры с неодно­родным распределением примесей является p-n -переход, представляющий собой об­ласть полупроводникового кристалла, в окрестности некоторой поверхности, по разные стороны которой преобладают до­норные и акцепторные примеси. Предпо­ложим, для простоты, что p-n -переход об­разуется в результате приведения в контакт идеально отполированных плоских по­верхностей полупроводниковых кристал­лов с различным типом проводимости. При этом вдоль оси ох, перпенди­кулярной плос­кости контакта, в окрестности точки х = 0 (рисунок 3 а) проис­ходит скачкообразное изменение концентрации примесей. В начальный мо­мент распределение концен­траций основных носителей соответствует рас­пределению концентраций примесей. Такое состояние является неравновес­ным и, вследствие наличия градиентов кон­центраций электронов и дырок, возникает их встречная диффузия, со­провождающаяся переносом заряда че­рез поверхность кон­такта и образова­нием областей простран­ственного за­ряда шириной в р – обла­сти и 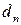в n –области (рисунок 3 б). и 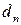об­ратны концентрациям примесей и сов­падают при их равенстве.

В результате диффузии электронов и дырок потенциал р – области понижа­ется, n – области – возрастает, т.е. ме­жду ними возникает разность потенциа­лов и электрическое поле с вектором напряженности, направленным в сто­рону р – области. Это внутреннее поле прекращает диффузию свободных носи­телей заряда. Примерный вид распреде­ления потенциала в окрестности p – n- пе­рехода показан на рисунке 3 в.

Типичное значение суммарной ширины областей пространственного заряда имеет величину 10^{– 6} – 10^{– 8}м. Изменение энергии электрона при переходе между областями 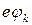- порядка ширины запрещенной зоны. Поэтому напряженность внутреннего поля составляет 10⁵ - 10⁷ В/м. Поскольку свободные носители заряда весьма подвижны, в равновесном состоянии их концентрация в той области, где существует электрическое поле очень мала. Примерный вид распределения концентрации свободных носителей заряда вблизи p – n- пе­рехода показан на рисунке 3 г.

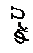
Таким образом, в области p – n- пе­рехода существует слой шириной 10^{– 6} – 10^{– 8}м, в котором концентрация носителей намного меньше, чем в однородных областях, расположенных вдали от перехода в обоих направлениях. Соответственно этот слой обладает большим сопротивлением, и всю систему можно рассматривать как электрическую цепь с последовательными

тремя сопротивлениями, в которой большое сопротивление помещено между двумя малыми. Поэтому внешнее напряжение , приложенное к системе, в основном падает в обедненном слое. Изменение потенциала в этом слое будет равно:

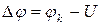. (3)

будем считать положительным, если напряженность внешнего поля направлена навстречу внутреннему. Изменение разности потенциалов в обедненном слое связано с изменением величины объемного заряда, его ширины и показано на рисунке 4. При приложении внешнего поля в прямом направлении ( > 0), объемный заряд и ширина обедненной области уменьшаются; при приложении внешнего поля в обратном направлении ( < 0), эти величины увеличиваются.

С энергетической точки зрения процессы, происходящие в области p – n- пе­рехода могут быть описаны следующим образом. Условием равновесия системы является вытекающее из термодинамических соображений требование постоянства уровня Ферми во всем объеме полупроводника. В исходном состоянии (рисунок 5 а) уровни Ферми в р и n областях не совпадают: 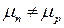. Вследствие диффузии основных носителей заряда потенциал р -области уменьшается, а потенциальная энергия электронов возрастает. Энергетические уровни р и n областей смещаются в противоположных направлениях до совпадения уровней Ферми в обеих областях – рисунок 5 б. Поэтому в равновесном состоянии электронам для перехода из n- области в р- область необходимо преодолеть потенциальный барьер высотой 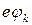, которая определяется разницей в положении уровней Ферми в р и n областях. Аналогичное утверждение

справедливо и для дырок р- области. Необходимо только учитывать, что потенциальная энергия дырок противоположна по знаку энергии электронов. Поэтому уменьшение потенциальной энергии электронов при переходе из р в n область означает ее увеличение для дырок.

Приложение к p – n- пе­реходу положительного (прямого, отпирающего) напряжения приводит к уменьшению потенциального барьера для перехода свободных носителей в смежную область: снимается запрет на встречную диффузию электронов и дырок, через переход протекает большой ток, его сопротивление мало – рисунок 5 в.

Отрицательное (обратное, запирающее) напряжение повышает потенциальный барьер для носителей заряда, вероятность прохождения через переход основных носителей заряда оказывается малой, сопротивление перехода очень велико – рисунок 5 г.

В отсутствие внешнего напряжения ток через переход равен нулю. Но это означает только то, что отсутствует перенос заряда через переход. При этом в каждом из направлений могут двигаться равные количества электронов и дырок.

Рассмотрим электронную составляющую тока через переход (имея в виду, что для дырочной составляющей справедливы совершенно аналогичные рассуждения). Она включает в себя две компоненты: электронный ток генерации и электронный ток рекомбинации . создается электронами, генерируемыми в р -области обедненного слоя в результате теплового возбуждения электронов с уровней валентной зоны в зону проводимости. Хотя концентрация таких электронов (неосновных носителей) в р -области очень мала, они играют важную роль в протекании тока через переход. Это обусловлено тем, что каждый электрон, попавший в обедненный слой, тут же перебрасывается в n -область сильным электрическим полем перехода. Поэтому величина тока генерации не зависит от изменения потенциала в обедненном слое.

Ток создается электронами n -области, движущимися в сторону р -области. Попав в р -область с большой концентрацией дырок электроны очень быстро рекомбинируют с ними, чем и объясняется название этого тока. Протеканию тока рекомбинации препятствует электрическое поле обедненного слоя. Поэтому в его создании принимают участие только те электроны, которые попадают на границу обедненного слоя из n -области, имея кинетическую энергию, достаточную для преодоления потенциального барьера. Вероятность преодоления электроном потенциального барьера высотой (а значит число таких электронов и величина ) пропорциональна, в соответствии с распределением Больцмана, 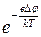. Поэтому

. (4)

В отсутствии внешнего напряжения (U = 0), т.е. в равновесном состоянии, устанавливается такая высота потенциального барьера 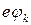, при которой ток генерации точно уравновешивает ток рекомбинации:

. (5)

Поэтому зависимость тока рекомбинации от внешнего напряжения можно представить в виде:

. (6)

Полный электронный ток из n -области в р -область равен разнице токов генерации и рекомбинации:

. (7)

Ток дырочной составляющей

. (8)

Поэтому полный ток через p – n- пе­реход:

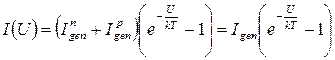. (9)

Выражение (9) аналитически описывает вольт-амперную характеристику p – n- пе­рехода, т.е. ВАХ полупроводникового диода. Примерный вид графика этой зависимости показан на рисунке 6.

 

⇐ Предыдущая78910111213141516

Поделиться:

Воспользуйтесь поиском по сайту: