 |
Электропроводность металлов
|
|
|
|
Напомним, что в квантовой механике электроны в кристаллах описываются волновыми функциями, представляющими собой плоские волны, которые распространяются во всех направлениях в кристалле. С этой точки зрения протекание электрического тока означает, что в некотором направлении распространяется больше волн, чем в противоположном. Строгий квантово-механический расчет показывает, что металл с идеальной, строго периодичной кристаллической решеткой не должен оказывать сопротивления протеканию электрического тока..
Однако в реальной кристаллической структуре всегда присутствуют нарушения периодичности, которые можно подразделить на два класса: нарушения периодичности, обусловленные наличием дефектов кристаллической структуры (атомы различных примесей, отсутствие атомов в некоторых узлах и т.п.), и нарушения, возникающие за счет участия атомов металла в тепловом колебательном движении. Взаимодействие электронов с ионами кристаллической решетки выражается в рассеянии электронных волн, что и является причиной существования электрического сопротивления металлов и его температурной зависимости.
Соответственно в удельном сопротивлении r металлов можно выделить два вклада:
 r = rкол + rпр (40.1)
r = rкол + rпр (40.1)
Зависящий от температуры вклад rкол = r (T) обусловлен несовершенствами решетки, возникающими вследствие участия атомов кристалла в тепловых колебаниях.
Независящий от температуры вклад  rприм ¹ rприм (T) обусловлен наличием в кристалле примесей и другими несовершенствами кристаллической структуры. Соответственно характерная зависимость удельного сопротивления металла от температуры имеет вид, показанный на рисунке.
rприм ¹ rприм (T) обусловлен наличием в кристалле примесей и другими несовершенствами кристаллической структуры. Соответственно характерная зависимость удельного сопротивления металла от температуры имеет вид, показанный на рисунке.
|
|
|
Обозначим концентрацию электронов в металле n, и назовем дрейфовойсреднюю скорость электронов:
 . (40.2)
. (40.2)
В отсутствии электрического поля 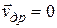 , электрический ток отсутствует. Внешнее поле с напряженностью
, электрический ток отсутствует. Внешнее поле с напряженностью 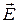 приводит к возникновению направленного движения электронов, переносу электрического заряда, т.е. электрического тока. Плотность тока пропорциональна скорости направленного движения
приводит к возникновению направленного движения электронов, переносу электрического заряда, т.е. электрического тока. Плотность тока пропорциональна скорости направленного движения 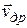 , а согласно закону Ома
, а согласно закону Ома  . Следовательно, дрейфовая скорость электронов пропорциональна
. Следовательно, дрейфовая скорость электронов пропорциональна 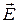 .
.
Пропорциональность 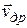 приложенной к электронам силе
приложенной к электронам силе  со стороны внешнего электрического поля возможна только в том случае, если кроме этой силы на электроны действует сила сопротивления среды, пропорциональная скорости:
со стороны внешнего электрического поля возможна только в том случае, если кроме этой силы на электроны действует сила сопротивления среды, пропорциональная скорости:
 . (40.3)
. (40.3)
Тогда уравнение движения электрона в кристаллеможно записать в виде:
 . (40.4)
. (40.4)
(Обратите внимание на то, что вместо массы электрона в уравнении стоит эффективная масса. Именно она характеризует отклик электронов на действие внешнего электрического поля.)
Из этого уравнения можно найти установившееся значение  и закон убывания
и закон убывания  после выключения поля.
после выключения поля.
Положим, что в некоторый момент времени внешнее электрическое поле выключается, т.е.  . Тогда уравнение движения электронов принимает вид:
. Тогда уравнение движения электронов принимает вид:
 . (40.5)
. (40.5)
Уравнение (40.5) решается разделением переменных. Решение имеет вид:
 . (40.6)
. (40.6)
Величина дрейфовой скорости за время
 . (40.7)
. (40.7)
уменьшается в e раз. Поэтому  называют временем релаксации, характеризующим процесс установления равновесия между электронной подсистемой и кристаллической решеткой.
называют временем релаксации, характеризующим процесс установления равновесия между электронной подсистемой и кристаллической решеткой.
Из (40.7) вытекает, что коэффициент сопротивления среды
 (40.8)
(40.8)
и уравнение движения электрона можно записать в виде:
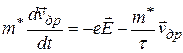 . (40.9)
. (40.9)
При установившемся значении силы тока  :
:
 . (40.10)
. (40.10)
Поэтому установившееся в поле значение дрейфовой скорости можно положить равным
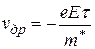 . (40.11)
. (40.11)
Следовательно, установившееся значение плотности тока
 . (40.11)
. (40.11)
Таким образом, можно считать, что выполняется закон Ома  , причем удельная электропроводность определяется соотношением:
, причем удельная электропроводность определяется соотношением:
|
|
|
 . (40.11)
. (40.11)
Напомним, что классическое выражение для  имеет вид:
имеет вид:
 . (40.11)
. (40.11)
где  есть время свободного пробега =
есть время свободного пробега =  .
.
Наиболее существенным отличием квантового подхода является использование  вместо m, а значит учет влияния периодического поля кристаллической решетки.
вместо m, а значит учет влияния периодического поля кристаллической решетки.
Кроме того, по классическим представлениям все электроны в электрическом поле изменяют скорость. В действительности это происходит только с электронами вблизи уровня Ферми.
Анализ, выходящий за рамки курса общей физики, показывает, что в квантовомеханической трактовке удельная электропроводность в соответствии с экспериментом оказывается обратно пропорциональной температуре кристалла.
Сверхпроводимость
 Исследование температурной зависимости сопротивления металлов в области низких температур показало, что при температурах в несколько кельвинов в ряде металлов и сплавов наблюдается переход в сверхпроводящее состояние. Этот переход происходить в очень узкой температурной области в окрестности характерной для каждого вещества температуры Ткр - критической температуры.
Исследование температурной зависимости сопротивления металлов в области низких температур показало, что при температурах в несколько кельвинов в ряде металлов и сплавов наблюдается переход в сверхпроводящее состояние. Этот переход происходить в очень узкой температурной области в окрестности характерной для каждого вещества температуры Ткр - критической температуры.
Экспериментально наблюдение перехода в сверхпроводящее состояние можно наблюдать, измеряя падение напряжения на проводнике, по которому протекает электрический ток. В области перехода падение напряжения скачком обращается в нуль.
Вторым способом является возбуждение в замкнутом (например, кольцевом) проводнике, перешедшем в сверхпроводящее состояние, кругового тока. Это можно сделать, если при охлаждении создать через поверхность, ограниченную проводником, магнитный поток внешнего магнитного поля. При выключении этого поля в сверхпроводящем кольце возникает замкнутый ток. Такой ток создает в окружающем пространстве магнитное поле, по величине которого можно судить о силе замкнутого тока. Экспериментально установлено, что ток в замкнутом кольце остается неизменным в течение примерно 2,5 лет. Этот факт позволил считать, что сопротивление сверхпроводника постоянному току не просто мало, а равно нулю.
Кроме обращения в нуль удельного сопротивления для сверхпроводников наблюдается эффект Мейснера, проявляющийся в том, что магнитное поле не проникает в толщу сверхпроводника и выталкивается из проводника при его переходе в сверхпроводящее состояние.
|
|
|
 Внешнее магнитное поле, индукция которого превышает некоторую Критическу в данных условиях величину
Внешнее магнитное поле, индукция которого превышает некоторую Критическу в данных условиях величину 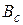 , разрушает сверхпроводящее состояние. Критическое поле может быть создано током, протекающим по проводнику, и это ограничивает величину тока, который может пропускать по сверхпроводнику.
, разрушает сверхпроводящее состояние. Критическое поле может быть создано током, протекающим по проводнику, и это ограничивает величину тока, который может пропускать по сверхпроводнику.
Величина коритической индукции зависит для данного проводника от температуры. При приближении температуры к температуре перехода в сверхпроводящее состояние 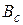 уменьшается и обращается нуль при Ткр.
уменьшается и обращается нуль при Ткр.
Сверхпроводимость есть макроскопический квантово-механический эффект. Объяснение сверхпроводимости было дано в теории БКШ (1959), разработанной Бардиным Купером и Шриффером. Основное представление этой теории сводится к тому, что электроны в сверхпроводнике объединяются в куперовские пары. Электроны пары имеют противоположно направленные спины, поэтому спин пары равны нулю. Частицы с нулевым спином являются бозонами, и куперовская пара электронов образует бозон. Бозоны склонны накапливаться в основном энергетическом состоянии. Куперовские пары, придя в согласованное движение, остаются в этом состоянии неопределенно долго и образуют незатухающий сверхпроводящий ток.
Образование пары не следует понимать буквально как слияние электронов. Расстояние между электронами пары 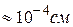 и
и  пар перекрываются.
пар перекрываются.
Представить наглядно квантовое взаимодействие электронов, образующих пару весьма сложно. Движущийся в кристалле электрон поляризует решетку, притягивая к себе положительные ионы. Внешне система электрон плюс положительный заряд окружающих его ионов создают электрическое поле соответствующее положительному заряду к которому может притягиваться другой электрон.
Ситуацию можно представлять и иначе. Положительный заряд в решетке созданный при движении данного электрона некоторое время сохраняется. Поэтому другой электрон притягивает другой электрон и облегчает его движение по траектории первого электрона. Во всяком случае, кристаллическая решетка играет существенную роль в образовании пары.
|
|
|
На квантовом языке взаимодействие посредствам кристаллической решетки означает обмен фононами. Электрон, движущийся в кристалле, изменяет режим колебаний решетки, – возбуждает фононы. Это возбуждение воспринимается другим электроном.
В результате электрон-фононного взаимодействия в куперовские пары объединяются электроны с противоположными импульсами и спинами.
Реальность образования пар проявляется в том, что для возбуждения электронной подсистемы кристалла находящегося в сверхпроводящем состоянии, надо разрушить хотя бы одну пару, затратив энергию связи  . Это есть минимальная энергия, которую может воспринять электронная подсистема. Следовательно, в энергетическом спектре сверхпроводящих электронов должна быть щель запрещенных значений энергии шириной
. Это есть минимальная энергия, которую может воспринять электронная подсистема. Следовательно, в энергетическом спектре сверхпроводящих электронов должна быть щель запрещенных значений энергии шириной  , которая обнаруживается экспериментально.
, которая обнаруживается экспериментально.
Из теории БКШ также вытекает, что магнитный поток, связанный со сверхпроводящим кольцом, должен быть кратным величине  , где q - заряд носителя тока. Т. е. магнитный поток, связанный с кольцом может изменяться только скачками. Это явление было обнаружено экспериментально, причем оказалось
, где q - заряд носителя тока. Т. е. магнитный поток, связанный с кольцом может изменяться только скачками. Это явление было обнаружено экспериментально, причем оказалось  , что подтвердило тот факт, что перенос заряда в сверхпроводнике осуществляется куперовскими парами.
, что подтвердило тот факт, что перенос заряда в сверхпроводнике осуществляется куперовскими парами.
Полупроводники
|
|
|


