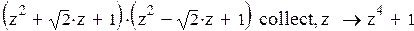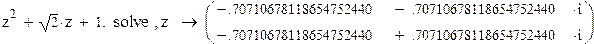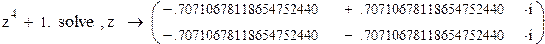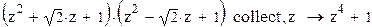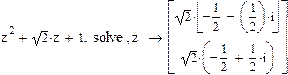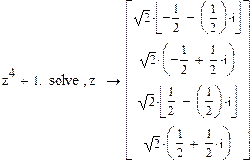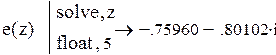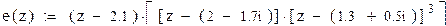|
Пример 6. Замечание. В Mathcad 14.0 вы получите тот же результат, но в показательной форме. Какой численный метод использует Mathcad для нахождения корней? К сожалению, фирма MathSoft не сообщает этого пользователю
|
|
|
|
Пример 6.

Если коэффициенты многочлена содержат десятичную точку, то символьный процессор получит указание найти численные значения корней и записать их, используя двадцатиразрядные числа.
Замечание. В Mathcad 14. 0 вы получите тот же результат, но в показательной форме.
Какой численный метод использует Mathcad для нахождения корней? К сожалению, фирма MathSoft не сообщает этого пользователю. (Вообще, «Руководство пользователя» и справочная система Mathcad ничего не сообщают о методах, используемых в работе символьного процессора. )
В целом, корни многочленов с действительными коэффициентами символьный процессор находит точнее, чем численный процессор.
Отметим одну деталь. Иногда при вычислении кратных корней символьный процессор сообщает пользователю только об одном из них (см. пример 7 ).
|
|
Пример 7.
|
|
|
|
|
|
Замечание. В Mathcad 14. 0 вы получите при решении того же примера следующий результат:
|
|
|
|
|
|
|
|
Если многочлен имеет комплексные коэффициенты, то использование оператора solve может не дать результата. До 14-той версии Mathcad при вычислении корней многочлена с комплексными коэффициентами оператор solve зачастую выдает только один корень. Но он может, вообще говоря, найти и все n корней (если многочлен ему понравится). (См. примеры 8 и 9 ).
|
|
Пример 8.
|
|
| Ограничим число разрядов в ответе: |
|
|
Оператор float, задающий число разрядов в получаемом символьным процессором результате, также как и оператор solve берется из палитры Symbolic.
Замечание. Mathcad 14. 0 в этом случае найдет все пять корней многочлена.
|
|
|
Пример 9.
| Дан многочлен: |
|
|
| Найдем его корни с помощью оператора solve: |
|
|
3. Проблемы при вычислении корней многочлена.
При использовании любого численного метода принципиально возможны два дефекта:
1) низкая точность вычисления корней;
2) зацикливание, когда вообще не удается получить результат.
Сложность задачи вычисления корней зависит от:
1) близости корней. Чем меньше расстояние между корнями, тем труднее задача.
2) степени многочлена. Чем выше степень, тем труднее получить значения всех корней с высокой точностью.
Задача вычисления корней многочлена очень чувствительна к изменению значений коэффициентов.
Рассмотрим два многочлена:
h1(z) = (z - 2)3 = 0 и h2(z) = (z - 2)3 – 10-6 = 0
Значения младших коэффициентов многочленов h1(z) и h2(z) различаются на 0. 000001. А значения корней –на 0. 01, причем два корня стали комплексными!
| h1(z) | h2(z) |
| z1 = 2 | z1 = 2. 0100 |
| z2 = 2 | z2 = 1. 9950 + i·0. 0087 |
| z3 = 2 | z3 = 1. 9950 - i·0. 0087 |
Итоговые упражнения.
1. Найти все коэффициенты многочлена: (x-2)·(x-3. 7)·(x-5) и представить его в канонической форме.
2. Найти все корни многочлена: 1. 7× x6 + 3. 8× x4 –5. 7× x3 + 1. 9× x2 – 0. 4× x +1. 1 = 0.
3. Найти все корни многочлена: z5-1=0 различными способами.
4. Найти все корни многочлена: z3+(3. 2-1. 4i)·z+1=0
Глава 6. Решение уравнений и систем уравнений.
В среде системы Mathcad можно искать решение уравнения (в том числе и нелинейного) как численными, так и аналитическими методами. Вы также можете найти решение системы уравнений (как линейных, так и нелинейных). Данная глава представляет собой введение в решение уравнений и систем уравнений численными методами.
1. Решение одного уравнения.
Mathcad позволяет найти с заданной точностью решение уравнения вида
f(x) = 0
где f(x) – некоторая известная функция. То есть, иначе говоря, найти с заданной точностью значение переменной x при котором f(x) обращается в ноль. Для этой цели служит встроенная функция root (f(x), x). Так как функция root использует для поиска решения итерационный метод, прежде чем вызвать ее надо задать начальное приближение.
|
|
|
При использовании функции root корень уравнения находится методом последовательного приближения. Процедура поиска решения заканчивается, когда два последних приближения отличаются друг от друга менее чем на величину TOL (см. главу 3 ). Причем вы можете уменьшить значение TOL, тем самым увеличив точность, с которой вычисляется корень уравнения (в этом случае вычисления потребуют больше времени).
Первый аргумент функции root – уравнение, решение которого надо найти, преобразованное так, чтобы в правой части был ноль. Второй аргумент этой функции – переменная, относительно которой надо искать решение.
Рассмотрим применение функции root в различных примерах.
 |
Пример 1.
При использовании функции root следует учитывать следующие правила:
1. Чтобы найти комплексный корень надо задать комплексное начальное приближение.
2. Если уравнение имеет несколько корней, результатом будет тот изи них, который расположен ближе к заданному начальному приближению.
Функция root может иметь еще два аргумента – границы интервала поиска решения, то есть root (f(x), x, a, b). Для того, чтобы решение было найдено, необходимо, чтобы f(а) было положительно, а f(b) - отрицательно (или наоборот). Для того, чтобы правильно выбрать интервал поиска решения или начальное приближение имеет смысл предварительно построить график. По этому графику вы сможете найти координаты точек пересечения кривых, описывающих правую и левую части уравнения или, если уравнение имеет вид f(x) = 0, координаты точек пересечения f(x) с осью абсцисс. (Построение двумерного графика и механизм считывания координат описаны в ч. II, гл. 1 ).
 |
Пример 2.
Если функция root не сходится, причиной этого может быть:
1. отсутствие корней;
2. локальный максимум или минимум между начальным приближением и корнем;
3. разрывы между начальным приближением и корнями;
4. корни уравнения далеко от начального приближения;
5. корень уравнения комплексный, а начальное приближение действительное (или наоборот).
|
|
|
2. Решение уравнений с параметром.
Пусть требуется найти несколько решений уравнения при изменении одного из его параметров. Например, найти решение уравнения

для нескольких различных значений параметра k. Самый простой способ состоит в определении функции
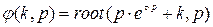
Чтобы решить уравнение для конкретного значения параметра k, задайте это значение или диапазон его изменения. Затем задайте начальное значение переменной p. После этого вы сможете найти искомое значение или несколько значений корня исходного уравнения, введя
j( k, p) =
Ответом будет значение или таблица значений корня уравнения (см. пример 3 ).
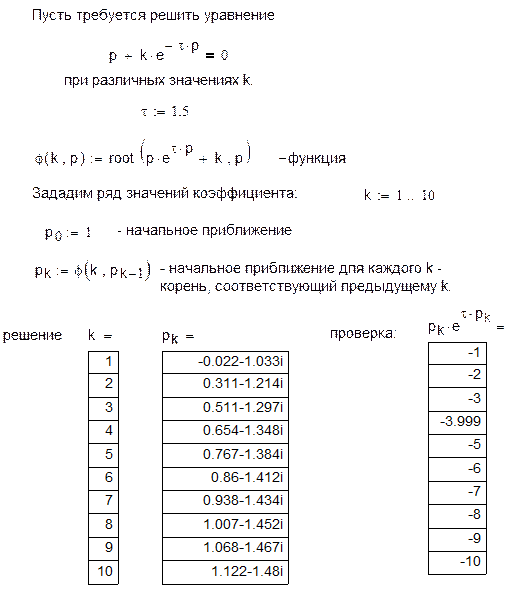 |
Пример 3.
 |
рис. 3. Траектория движения корня уравнения при изменении параметра.
|
|
|