Главная | Обратная связь | Поможем написать вашу работу!

Расчет средних показателей

МОДЕЛИРОВАНИЕ ЭКОСИСТЕМ

методические указания к практическим занятиям и лабораторным работам для подготовки дипломированных специалистов по направлению

656200 «Лесное хозяйство и ландшафтное строительство»

Брянск 2012

Брянская государственная инженерно-технологическая академия

Кафедра лесоустройства

Утверждены научно-методическим советом БГИТА Протокол № 11 от «24» декабря 2004 г.

МОДЕЛИРОВАНИЕ ЭКОСИСТЕМ

656200 «Лесное хозяйство и ландшафтное строительство»

Брянск 2012

Составитель: доцент каф. лесоустройства
канд. с.-х. наук Соломников А.А.

Рецензент: доцент каф. лесозащиты и охотоведения
доктор с.-х. наук Шелухо В.П.

Рекомендованы редакционно-издательской, научно-методической комиссиями лесохозяйственного факультета.

Протокол № 87 от «25» октября 2004 г.

Введение

Системный подход к изучению сложных биологических объектов получил уже широкое распространение, как в научных исследованиях, так и в практической деятельности лесохозяйственной отрасли. В основе такого подхода лежит рассмотрение природных объектов как комплекса взаимосвязанных элементов, каждый из которых связан со своим окружением.

В рамках системного подхода особое место занимает построение разнообразных моделей. Спецификой данного раздела определяется, что к построению модели можно приступать только тогда, когда получены знания об исходном объекте всеми доступными способами.

Моделью называется такая материально реализованная или представляемая система, которая отображает исходный объект таким образом, что изучение ее позволяет получить новые знания об исходном объекте.

Существует множество типов и разновидностей моделей, отличающихся особенностями строения, создания, использования, подробности и т.д. В лесном хозяйстве чаще всего используются имитационные математические модели, основанные на большом количестве наблюдений, что позволяет достигать высокой точности при прогнозировании процессов в системах, имеющих стохастическую природу, то есть в таких, где предсказать поведение отдельных элементов с достаточной достоверностью невозможно.

Практическая работа. Получение индивидуального задания

В качестве индивидуального задания для моделирования используются данные переобмера деревьев в насаждении по пяти показателям. Для установления взаимосвязи между показателями выбираются два из них. Один показатель принимается за х, другой за у. Основанием для выбора показателей служит последняя цифра номера зачетной книжки студента.

Таблица 1

Вспомогательная таблица для определения варианта задания

Последняя цифра шифра
Показатель ряда x	D	H	g	D	H	g	D	H	V	D
Показатель ряда y	H	g	f	g	f	V	f	V	f	V

Таким образом определяем, какие данные необходимо выписывать из приложения. Поскольку в реальной практической деятельности количество наблюдений может варьировать в достаточно широких пределах, для индивидуального задания берется разное количество данных. Оно определяется в зависимости от двух последних цифр номера зачетной книжки. Эти две цифры – это номер дерева, с которого нужно начинать выписывать данные по показателям, определенным ранее.

В дальнейшем в методических указаниях все расчеты будут показаны на примере для варианта 63. Но количество данных уменьшено по сравнению с реальным заданием. В качестве показателя х в этом случае мы принимаем диаметр дерева (D), а в качестве показателя у – площадь сечения g.

Исходные данные

Таблица 2

Ведомость обмера деревьев

№	х(D,см)	у(g, м²)	№	х(D,см)	у(g, м²)	№	х(D,см)	у(g, м²)
	15,6	0,0191		17,3	0,0235		14,6	0,0167
	15,2	0,0182		11,3	0,0101		16,3	0,0208
	21,1	0,0350		13,5	0,0143		19,6	0,0302
	15,9	0,0198		20,9	0,0343		15,0	0,0177
	12,0	0,0113		9,2	0,0066		19,2	0,0290
	15,6	0,0191		15,0	0,0177		16,9	0,0224
	20,4	0,0327		15,6	0,0191		13,5	0,0143
	21,2	0,0353		18,6	0,0271		19,0	0,0284
	20,5	0,0330		13,7	0,0147		19,1	0,0286
	11,7	0,0107		17,9	0,0251		16,3	0,0208
	20,8	0,0340		11,7	0,0107		18,6	0,0271
	15,0	0,0177		20,0	0,0314		11,3	0,0101
	20,9	0,0343		10,4	0,0085		16,6	0,0216
	17,2	0,0232		23,0	0,0416		18,6	0,0271
	18,1	0,0257		16,6	0,0216		15,2	0,0182
	18,7	0,0275		13,8	0,0150		17,4	0,0238
	9,5	0,0071		16,3	0,0208		14,7	0,0170
	17,2	0,0232		11,6	0,0106		18,5	0,0269
	19,1	0,0286		13,3	0,0139		16,1	0,0203
	15,5	0,0189		21,2	0,0353		18,1	0,0257
	10,0	0,0078		14,0	0,0154		17,2	0,0232
	13,0	0,0132		12,7	0,0127		17,6	0,0243
	16,1	0,0203		14,2	0,0159		17,6	0,0243
	17,2	0,0232		16,9	0,0224		18,9	0,0281
	17,2	0,0232		11,1	0,0097		14,0	0,0154
	15,3	0,0184		17,2	0,0232		12,2	0,0117
	11,8	0,0109		18,9	0,0281		23,0	0,0416
	11,4	0,0102		13,0	0,0132		15,7	0,0194
	14,3	0,0161		15,3	0,0184		15,6	0,0191
	19,8	0,0308		13,9	0,0152		19,9	0,0311
	14,4	0,0163		18,3	0,0263		17,8	0,0249
	18,2	0,0260		13,4	0,0141		21,8	0,0373
	14,0	0,0154		14,6	0,0167		20,0	0,0314
	14,4	0,0163		15,6	0,0191		10,7	0,0090
	13,3	0,0139		9,9	0,0077		13,8	0,0150
	14,8	0,0172		20,4	0,0327		13,3	0,0139
	14,6	0,0167		15,5	0,0189		17,6	0,0243
	19,6	0,0302		18,2	0,0260		12,5	0,0123
	11,1	0,0097		19,4	0,0296		12,0	0,0114
	16,6	0,0216		11,2	0,0099		12,2	0,0117
	17,3	0,0235		20,9	0,0343		11,7	0,0107
	16,3	0,0208		20,7	0,0336		14,0	0,0162
	13,3	0,0139		15,3	0,0183		12,0	0,0114
	13,3	0,0139		19,0	0,0284		15,3	0,0184
	19,5	0,0298		15,1	0,0179		13,9	0,0152
	13,7	0,0147		16,4	0,0211		20,7	0,0336
	16,9	0,0224		24,3	0,0463		14,3	0,0161
	15,7	0,0194		15,7	0,0194		12,5	0,0123
	18,6	0,0271		14,7	0,0170

Данная ведомость будет служить исходными данными для всех дальнейших расчетов. Некоторые расчеты будут дублироваться различными методами и служить своего рода проверочными данными для предыдущих вычислений.

Расчет средних показателей

Наиболее распространенным и используемым средним показателем является среднеарифметическая величина. Она рассчитывается по формуле:

где N – количество данных, среди которых находится среднее значение.

Но для вычисления средней площади и ряда других показателей (средний объем, запас и т.д.) более оправдано применение средней квадратической величины:

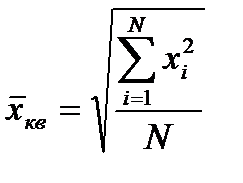
Для нашего примера рассчитываем:

åx=2332,0

åу²=0,07289

12 3 4 5 6 7 8 9 Следующая ⇒

Воспользуйтесь поиском по сайту: