 |
Расчет центральных и основных моментов
|
|
|
|
Центральные моменты рассчитываются с использованием начальных.
Центральный момент первой степени всегда равен нулю, поскольку вычисляется как 
Центральный момент второй степени рассчитывается через начальные моменты по формуле:
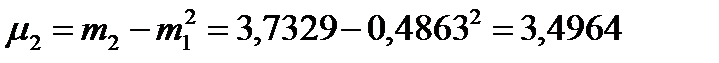
Центральный момент третьей степени рассчитывается через начальные моменты по формуле:

Центральный момент четвертой степени рассчитывается через начальные моменты по формуле:

Для практического применения рассчитываются основные моменты статистических величин, которые характеризуют отклонение фактических данных от нормального типа распределения:
 ;
;  ;
; 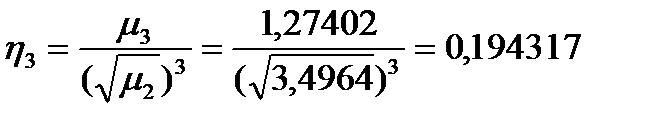

Основной момент третьей степени характеризует асимметричность распределения, а основной момент четвертой степени – крутость графика распределения.
Практическая работа. Расчет статистических характеристик при помощи моментов
При помощи моментов статистических величин легко рассчитать все основные характеристики вариационного ряда.
1. Средняя арифметическая величина:
 ,
,
где Ах – условное среднее значение (см. расчет начальных моментов);
k – размер класса по ряду х (см. разбивка большой выборки на классы);
m1 – начальный момент первой степени.
2. Показатели изменчивости выборочной совокупности:
- дисперсия учитывает отклонение каждого из значений выборки от среднеарифметической величины:

- основное отклонение представлено в тех же единицах измерения, что и среднеарифметическая величина и рассчитывается в двух вариантах:
а) неполное – без учета размера класса

б) полное – с учетом размера класса

- коэффициент изменчивости представлен в процентном выражении и позволяет судить о степени изменчивости вне зависимости от абсолютных значений выборки:
|
|
|

По величине коэффициента изменчивости можно сделать вывод о степени вариации в пределах выборки. Общеприняты следующие придержки: C≤10% - низкое варьирование; 10%<C≤30% - среднее варьирование; C>30% - высокое варьирование. На основании этих придержек следует сделать вывод о степени варьирования. В данном примере мы имеем среднюю степень изменчивости в выборке.
3. Показатели отклонения графика от нормального распределения.
График нормального распределения имеет колоколообразный вид и симметричен относительно среднеарифметического значения. Но идеальная форма нормального распределения встречается редко. Как правило, график отклоняется вправо или влево, а также вверх или вниз.
- асимметрия характеризует отклонение графика вправо или влево от средней величины.

- эксцесс характеризует крутость графика распределения

4. Точность опыта показывает, можно ли доверять результатам, полученным при данном коэффициенте изменчивости по данному количеству наблюдений.

Показатель точности опыта до 1% - очень высокий, до 5% - высокий, до 10% - нормальный.
5.Основные ошибки статистических величин показывают пределы возможного отклонения выборочных показателей от одноименных показателей генеральной совокупности:
- основная ошибка средней величины:

- основная ошибка среднеквадратического отклонения:

- основная ошибка асимметрии:
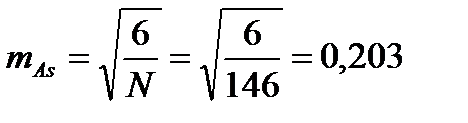
- основная ошибка эксцесса:

6. Достоверность показателей оценивается по соотношению значения показателя и величины его основной ошибки. Показатель считается достоверным, при значении критерия больше 3.
- критерий достоверности среднеарифметической величины:
 ;
;
- критерий достоверности среднеквадратического отклонения:
 ;
;
- критерий достоверности асимметрии:
 ;
;
- критерий достоверности эксцесса:

|
|
|
|
|
|


