 |
Расчет теоретических частот по распределению типа В
|
|
|
|
При этом типе распределения абсолютное значение асимметрии превышает 0,75-0,80, при критерии достоверности более 2.
Теоретические частоты при распределении типа В рассчитываются по формуле:
В этой формуле используется численность вариационного ряда и функция распределения типа В:
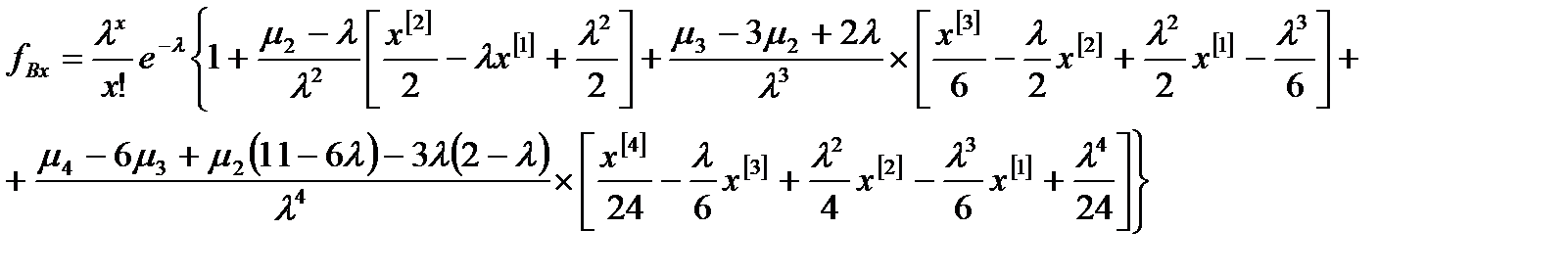
В этой формуле использованы значения центральных моментов (m) и первый начальный момент относительно нулевого значения (l). Функция распределения типа В весьма сложна и ее расчет целесообразно производить с применением компьютера и электронных таблиц. В этом случае необходимо рассчитать таблицу
Таблица 9
Расчет частот теоретического распределения по типу В
| x | x’ | n | S1 | λ | Pm | 0,537743 | +0,200643 ´ x[1] | -0,02096 ´ x[2] | -8,54373 ´10-5 ´ x[3] | -2,05585 ´10-5 ´ x[4] | = Σ | fB(X) =Pm(Σ) | nI=N*fB(X) |
| 8,25 | ---- | 4,4863 | 0,011262 | 0,537743 | 0,53774 | 0,00605 | 0,8842 | ||||||
| 9,95 | 0,050526 | 0,537743 | 0,20064 | 0,73839 | 0,03730 | 5,4469 | |||||||
| 11,65 | 0,113337 | 0,537743 | 0,40129 | -0,04192 | 0,89711 | 0,10167 | 14,8446 | ||||||
| 13,35 | 0,169488 | 0,537743 | 0,60193 | -0,12576 | -0,00051 | 1,01340 | 0,17176 | 25,0769 | |||||
| 15,05 | 0,190093 | 0,537743 | 0,80257 | -0,25151 | -0,00205 | -0,00049 | 1,08626 | 0,20649 | 30,1476 | ||||
| 16,75 | 0,170563 | 0,537743 | 1,00321 | -0,41918 | -0,00513 | -0,00247 | 1,11418 | 0,19004 | 27,7455 | ||||
| 18,45 | 0,127533 | 0,537743 | 1,20386 | -0,62878 | -0,01025 | -0,00740 | 1,09517 | 0,13967 | 20,3918 | ||||
| 20,15 | 0,081736 | 0,537743 | 1,40450 | -0,88029 | -0,01794 | -0,01727 | 1,02674 | 0,08392 | 12,2526 | ||||
| 21,85 | 0,045836 | 0,537743 | 1,60514 | -1,17372 | -0,02871 | -0,03454 | 0,90592 | 0,04152 | 6,0625 | ||||
| 23,55 | 0,022848 | 0,537743 | 1,80579 | -1,50906 | -0,0431 | -0,06217 | 0,72924 | 0,01666 | 2,4326 | ||||
| 25,25 | 0,01025 | 0,537743 | 2,00643 | -1,88633 | -0,06151 | -0,10361 | 0,49271 | 0,00505 | 0,7374 | ||||
| 146,0226 |
|
|
|
В этой таблице значения получены:
x’ – условные значения классов. Принимаются равным 0 для наименьшего класса с последующим увеличением.
S1 - последовательная сумма частот, начиная с наибольшего (последнего) класса;
λ – начальный момент относительно нулевого значения:
Pm – фрагмент функции распределения В:
коэффициенты для колонок 7-11 получены по следующим формулам:
для колонки 7:
для колонки 8:
для колонки 9:
для колонки 10:
для колонки 11:
Значения x[1] - x[4] вычислены по формулам:
x[1]=x’; x[2]=x’´(x’-1); x[3]=x’´(x’-1) ´(x’-2); x[4]=x’´(x’-1) ´(x’-2) ´(x’-3)
Колонка 12 представляет собой сумму по колонкам с 7 по 11. Дальнейшие расчеты пояснений не требуют.
Проверкой правильности выполнения расчетов служит сумма по колонке теоретических частот, которая приблизительно должна равняться численности вариационного ряда.
Для всех приведенных выше видов теоретического распределения можно утверждать, что правильность выполнения расчетов и совпадение теоретической и фактической численности вариационного ряда не является гарантией того, что данный тип распределения достоверно отражает фактические данные. Для проверки правильности выбора теоретического распределения необходимо рассчитать критерий согласия теоретических частот с фактическими – критерий Пирсона.
Практическая работа. Расчет критерия согласия Пирсона
Критерий согласия учитывает расхождения отдельных значений частот классов и таким образом свидетельствует о том, насколько близки два распределения. Он может быть применен как для сравнения двух фактических вариационных рядов, так и для установления правильности выбора теоретического распределения.
В том случае, если значение критерия согласия не превышает табличного значения, различия между рядами распределения признаются несущественными.
|
|
|
Для оценки расхождения фактического и теоретического распределения табличное значение критерия согласия принимается равным 2.
Критерий согласия рассчитывается по формуле:
, где К – количество классов включая добавленные при расчете теоретического распределения.
Расчет выполняется в форме таблицы:
Таблица 10
Расчет критерия согласия теоретических частот с фактическими
| х | n | n` | n-n` | (n-n`)2 | 
|
| 8,25 | 1,752 | -1,752 | 3,070 | 1,752 | |
| 9,95 | 5,479 | 0,521 | 0,272 | 0,050 | |
| 11,65 | 12,869 | 5,131 | 26,324 | 2,045 | |
| 13,35 | 22,711 | -0,711 | 0,506 | 0,022 | |
| 15,05 | 30,112 | 0,888 | 0,789 | 0,026 | |
| 16,75 | 29,994 | -4,994 | 24,940 | 0,836 | |
| 18,45 | 22,446 | -2,446 | 5,983 | 0,267 | |
| 20,15 | 12,620 | 4,380 | 19,187 | 1,520 | |
| 21,85 | 5,330 | -1,330 | 1,770 | 0,332 | |
| 23,55 | 1,692 | 1,308 | 1,712 | 1,012 | |
| 25,25 | 0,403 | -0,403 | 0,163 | 0,403 | |
| 145,408 | 8,262 |
В нашем случае критерий согласия Пирсона не превышает табличного значения, что свидетельствует о незначительных расхождениях в сравниваемых вариационных рядах, а также о том, что теоретическое распределение было подобрано верно.
|
|
|
