 |
Метод избранных координат точек
|
|
|
|
Для использования этого метода требуется график. Мы используем график корреляции. По графику, учитывая вес точек, проводится сглаживающая усредняющая линия – прямая.
С прямой снимаются отсчеты зависимой переменной по двум значениям независимой. При этом точки должны отстоять друг от друга как можно дальше – это повышает точность получаемого уравнения.
Снятые значения для переменных:
х1 =9,95 у1= 0,0070
х2 =23,55 у2= 0,0399
Уравнение прямой в имеет следующий вид:
у = a + bx
Для получения частной модели необходимо решить систему из двух уравнений:

Таким образом, частная модель будет иметь вид:
у = 0,00242 х – 0,0171
Проверка адекватности уравнения
Для проверки адекватности необходимо сравнить фактические значения у и значения, вычисленные по уравнению. Значения уфакт берутся из таблицы распределения вариант.
Таблица 17
Проверка адекватности уравнения взаимосвязи
| х | nх | увыч | уфакт | уфакт-увыч | (уфакт-увыч)2nх | 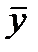
| уфакт- 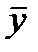
| (уфакт- 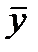 )2nх )2nх
|
| 9,95 | 0,0070 | 0,009 | 0,0019 | 0,00002 | -0,0116 | 0,00081 | ||
| 11,65 | 0,0111 | 0,010 | -0,0011 | 0,00002 | -0,0105 | 0,00198 | ||
| 13,35 | 0,0152 | 0,014 | -0,0013 | 0,00004 | -0,0066 | 0,00096 | ||
| 15,05 | 0,0193 | 0,018 | -0,0011 | 0,00004 | -0,0022 | 0,00016 | ||
| 16,75 | 0,0234 | 0,023 | -0,0009 | 0,00002 | 0,02050 | 0,0020 | 0,00010 | |
| 18,45 | 0,0275 | 0,027 | -0,0004 | 0,00000 | 0,0066 | 0,00088 | ||
| 20,15 | 0,0317 | 0,032 | -0,0001 | 0,00000 | 0,0110 | 0,00207 | ||
| 21,85 | 0,0358 | 0,035 | -0,0006 | 0,00000 | 0,0146 | 0,00086 | ||
| 23,55 | 0,0399 | 0,044 | 0,0040 | 0,00005 | 0,0234 | 0,00164 | ||
| 0,00019 | 0,00946 |

Уравнение считается адекватным при значении показателя тесноты связи больше 0,97.
Следовательно, уравнение, полученное методом избранных координат точек адекватно и хорошо отражает фактические данные.
|
|
|
Метод статистических характеристик
Уравнение взаимосвязи может быть получено также и при помощи статистических характеристик.
Для этого используется следующая формула:

Подставив в это уравнение известные статистические характеристики, получим:

Таблица 18
Проверка адекватности уравнения
| х | nх | увыч | уфакт | уфакт-увыч | (уфакт-увыч)2nх | 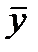
| уфакт- 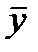
| (уфакт- 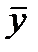 )2nх )2nх
|
| 9,95 | 0,0087 | 0,009 | 0,0002 | 0,00000 | -0,0116 | 0,00081 | ||
| 11,65 | 0,0121 | 0,010 | -0,0021 | 0,00008 | -0,0105 | 0,00198 | ||
| 13,35 | 0,0156 | 0,014 | -0,0017 | 0,00006 | -0,0066 | 0,00096 | ||
| 15,05 | 0,0190 | 0,018 | -0,0007 | 0,00002 | -0,0022 | 0,00016 | ||
| 16,75 | 0,0224 | 0,023 | 0,0001 | 0,00000 | 0,02050 | 0,0020 | 0,00010 | |
| 18,45 | 0,0259 | 0,027 | 0,0013 | 0,00003 | 0,0066 | 0,00088 | ||
| 20,15 | 0,0293 | 0,032 | 0,0023 | 0,00009 | 0,0110 | 0,00207 | ||
| 21,85 | 0,0327 | 0,035 | 0,0024 | 0,00002 | 0,0146 | 0,00086 | ||
| 23,55 | 0,0362 | 0,044 | 0,0077 | 0,00018 | 0,0234 | 0,00164 | ||
| 0,00048 | 0,00946 |
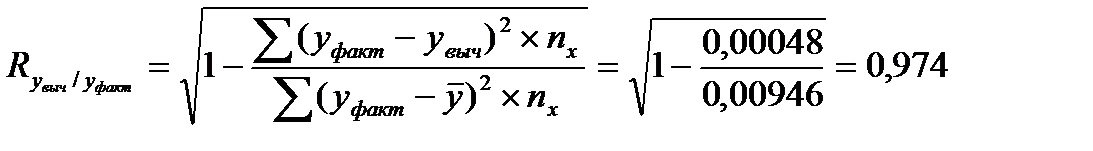
Уравнение считается адекватным при значении показателя тесноты связи больше 0,97. Следовательно, уравнение, полученное методом статистических характеристик адекватно и хорошо отражает фактические данные.
Лабораторная работа. Метод наименьших квадратов
Метод наименьших квадратов позволяет получить уравнение регрессии без использования графика. График необходим только для определения типа уравнения.
По данному методу рассчитываются уравнения практически любой сложности. Для получения коэффициентов уравнения необходимо рассчитать одну из приведенных систем:
Для уравнения у = а + bx

Для уравнения у = а + bx + cx2
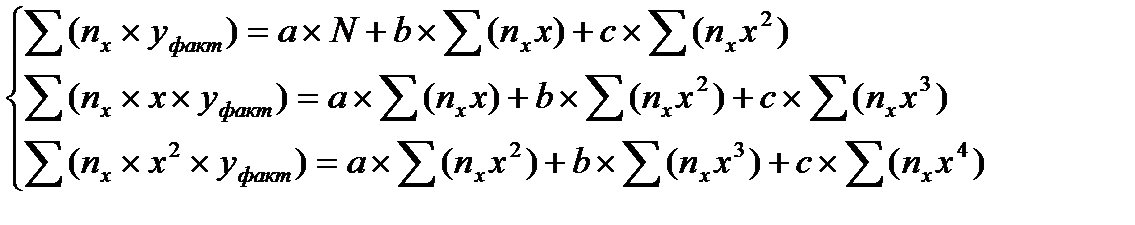
Для уравнения у = а + bx + cx2 + dx3
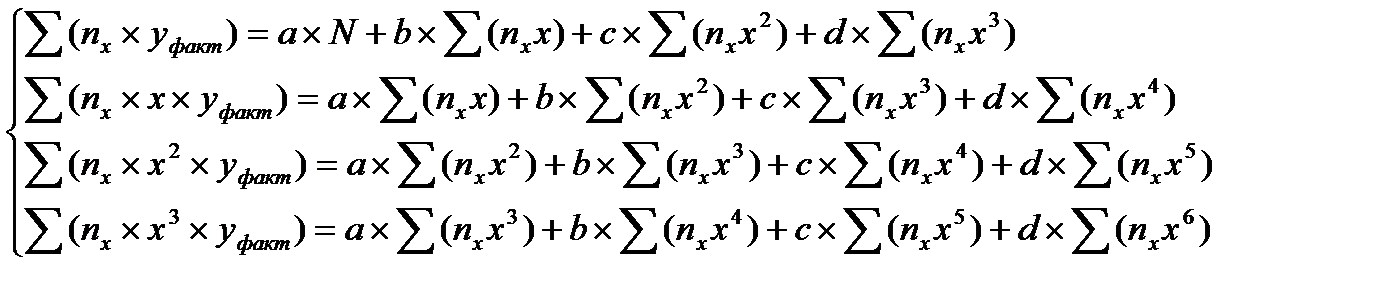
В зависимости от сложности необходимого уравнения составляется таблица сумм, в которой рассчитываются суммы, используемые в системе уравнений.
В нашем примере достаточным является уравнение кривой второго порядка: у = а + bx + cx2
Таблица 19
Расчет сумм квадратов
| х | nх | nхx | уфакт | nхyфакт | nхxyфакт | nхx2 | nхx2yфакт | nхx3 | nхx4 |
| 9,95 | 59,70 | 0,0089 | 0,0534 | 0,53133 | 594,01500 | 5,28673 | 5910,449 | 58808,970 | |
| 11,65 | 209,70 | 0,0100 | 0,1802 | 2,09933 | 2443,00500 | 24,45719 | 28461,008 | 331570,746 | |
| 13,35 | 293,70 | 0,0139 | 0,3058 | 4,08243 | 3920,89500 | 54,50044 | 52343,948 | 698791,709 | |
| 15,05 | 466,55 | 0,0183 | 0,5659 | 8,51680 | 7021,57750 | 128,17776 | 105674,741 | 1590404,858 | |
| 16,75 | 418,75 | 0,0225 | 0,5625 | 9,42188 | 7014,06250 | 157,81641 | 117485,547 | 1967882,910 | |
| 18,45 | 369,00 | 0,0272 | 0,5430 | 10,01835 | 6808,05000 | 184,83856 | 125608,523 | 2317477,240 | |
| 20,15 | 342,55 | 0,0315 | 0,5363 | 10,80645 | 6902,38250 | 217,74987 | 139083,007 | 2802522,599 | |
| 21,85 | 87,40 | 0,0352 | 0,1406 | 3,07211 | 1909,69000 | 67,12560 | 41726,727 | 911728,974 | |
| 23,55 | 70,65 | 0,0439 | 0,1317 | 3,10154 | 1663,80750 | 73,04115 | 39182,667 | 922751,799 | |
| S | 0,211313 | 3,0194 | 51,6502 | 38277,485 | 912,9937 | 655476,617 | 11601939,8 |
|
|
|
Подставив значения в систему уравнений, получим:

Решив эту систему уравнений мы получим три коэффициента:
а = -0,00438
b = 0,000602
c = 0,000059
Таким образом, уравнение регрессии будет иметь вид:
у = 0,000059х2 + 0,000602х – 0,00438
Таблица 20
Проверка адекватности уравнения
| х | nх | увыч | уфакт | уфакт-увыч | (уфакт-увыч)2nх | 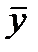
| уфакт- 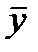
| (уфакт- 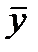 )2nх )2nх
|
| 9,95 | 0,0075 | 0,0089 | 0,0014 | 0,000012 | -0,01160 | 0,000808 | ||
| 11,65 | 0,0107 | 0,0100 | -0,0006 | 0,000008 | -0,01049 | 0,001981 | ||
| 13,35 | 0,0142 | 0,0139 | -0,0003 | 0,000002 | -0,00660 | 0,000959 | ||
| 15,05 | 0,0181 | 0,0183 | 0,0002 | 0,000001 | -0,00225 | 0,000157 | ||
| 16,75 | 0,0223 | 0,0225 | 0,0002 | 0,000001 | 0,02050 | 0,00200 | 0,000100 | |
| 18,45 | 0,0269 | 0,0272 | 0,0003 | 0,000002 | 0,00665 | 0,000884 | ||
| 20,15 | 0,0318 | 0,0315 | -0,0002 | 0,000001 | 0,01104 | 0,002074 | ||
| 21,85 | 0,0370 | 0,0352 | -0,0019 | 0,000014 | 0,01465 | 0,000858 | ||
| 23,55 | 0,0426 | 0,0439 | 0,0013 | 0,000005 | 0,02340 | 0,001642 | ||
| 0,000045 | 0,009462 |

Уравнение считается адекватным при значении показателя тесноты связи больше 0,97. Следовательно, уравнение, полученное методом наименьших квадратов адекватно и хорошо отражает фактические данные.
Приложения
Приложение 1
Ведомость обмера деревьев
| № дерева | Диаметр D, см | Высота h, м | Площадь сечения g, м2 | Видовое число, f | Объем, V, м3 |
| 12,8 | 13,3 | 0,0129 | 0,446 | 0,094 | |
| 10,2 | 13,6 | 0,0082 | 0,571 | 0,062 | |
| 13,4 | 13,9 | 0,0141 | 0,446 | 0,107 | |
| 13,6 | 14,1 | 0,0145 | 0,446 | 0,111 | |
| 15,5 | 14,5 | 0,0189 | 0,403 | 0,146 | |
| 13,3 | 14,2 | 0,0139 | 0,459 | 0,108 | |
| 9,4 | 12,7 | 0,0069 | 0,579 | 0,050 | |
| 9,7 | 14,0 | 0,0074 | 0,618 | 0,058 | |
| 13,3 | 14,3 | 0,0139 | 0,464 | 0,108 | |
| 15,1 | 13,8 | 0,0179 | 0,391 | 0,133 | |
| 14,1 | 13,9 | 0,0156 | 0,425 | 0,118 | |
| 12,4 | 13,8 | 0,0121 | 0,476 | 0,092 | |
| 8,7 | 12,5 | 0,0059 | 0,618 | 0,043 | |
| 13,0 | 14,3 | 0,0133 | 0,481 | 0,105 | |
| 12,0 | 13,9 | 0,0113 | 0,464 | 0,082 | |
| 12,3 | 13,4 | 0,0119 | 0,468 | 0,088 | |
| 8,7 | 12,7 | 0,0059 | 0,627 | 0,043 | |
| 11,3 | 14,5 | 0,0100 | 0,549 | 0,085 | |
| 14,4 | 13,9 | 0,0163 | 0,416 | 0,122 | |
| 19,6 | 14,7 | 0,0302 | 0,322 | 0,230 | |
| 10,5 | 12,8 | 0,0087 | 0,524 | 0,062 | |
| 12,8 | 13,3 | 0,0129 | 0,446 | 0,094 | |
| 11,8 | 12,8 | 0,0109 | 0,464 | 0,078 | |
| 13,3 | 13,0 | 0,0139 | 0,421 | 0,099 | |
| 10,9 | 13,0 | 0,0094 | 0,511 | 0,068 | |
| 9,8 | 12,0 | 0,0075 | 0,524 | 0,052 | |
| 13,4 | 12,5 | 0,0141 | 0,399 | 0,097 | |
| 14,5 | 13,6 | 0,0165 | 0,403 | 0,122 | |
| 11,0 | 12,5 | 0,0095 | 0,489 | 0,067 | |
| 21,0 | 14,9 | 0,0346 | 0,305 | 0,265 | |
| 9,9 | 13,1 | 0,0077 | 0,567 | 0,057 | |
| 14,4 | 13,8 | 0,0163 | 0,412 | 0,122 | |
| 14,0 | 13,9 | 0,0154 | 0,425 | 0,116 | |
| 10,9 | 14,1 | 0,0093 | 0,554 | 0,073 | |
| 15,6 | 14,4 | 0,0191 | 0,395 | 0,147 | |
| 16,8 | 14,9 | 0,0222 | 0,382 | 0,175 | |
| 13,2 | 15,1 | 0,0137 | 0,489 | 0,113 | |
| 16,3 | 14,5 | 0,0209 | 0,382 | 0,161 | |
| 11,8 | 14,7 | 0,0109 | 0,536 | 0,088 | |
| 11,7 | 14,1 | 0,0107 | 0,519 | 0,084 | |
| 9,3 | 13,3 | 0,0068 | 0,614 | 0,051 | |
| 14,0 | 13,8 | 0,0154 | 0,425 | 0,115 | |
| 13,7 | 14,4 | 0,0127 | 0,485 | 0,100 | |
| 13,8 | 13,8 | 0,0150 | 0,429 | 0,112 | |
| 9,8 | 13,0 | 0,0075 | 0,571 | 0,056 | |
| 11,9 | 13,9 | 0,0111 | 0,502 | 0,085 | |
| 12,1 | 13,5 | 0,0115 | 0,481 | 0,086 | |
| 16,7 | 14,5 | 0,0219 | 0,373 | 0,168 | |
| 13,2 | 13,9 | 0,0137 | 0,451 | 0,104 | |
| 11,8 | 14,0 | 0,0109 | 0,511 | 0,085 | |
| 10,1 | 12,6 | 0,0080 | 0,536 | 0,057 | |
| 10,4 | 12,7 | 0,0084 | 0,524 | 0,061 | |
| 11,6 | 13,0 | 0,0106 | 0,481 | 0,077 | |
| 13,3 | 14,1 | 0,0139 | 0,455 | 0,107 | |
| 12,3 | 14,3 | 0,0119 | 0,498 | 0,093 | |
| 12,0 | 13,8 | 0,0113 | 0,494 | 0,086 | |
| 13,6 | 14,9 | 0,0145 | 0,472 | 0,117 | |
| 14,4 | 14,2 | 0,0163 | 0,425 | 0,125 | |
| 14,6 | 14,6 | 0,0167 | 0,429 | 0,132 | |
| 10,7 | 13,2 | 0,0090 | 0,528 | 0,067 | |
| 12,9 | 13,0 | 0,0131 | 0,433 | 0,093 | |
| 8,9 | 12,8 | 0,0062 | 0,618 | 0,046 | |
| 12,9 | 13,9 | 0,0131 | 0,464 | 0,100 | |
| 12,0 | 13,8 | 0,0113 | 0,494 | 0,086 | |
| 11,7 | 14,3 | 0,0107 | 0,524 | 0,085 | |
| 16,2 | 14,3 | 0,0206 | 0,378 | 0,157 | |
| 12,2 | 13,5 | 0,0117 | 0,476 | 0,087 | |
| 9,2 | 12,5 | 0,0067 | 0,584 | 0,048 | |
| 12,0 | 13,5 | 0,0113 | 0,481 | 0,084 | |
| 15,7 | 14,1 | 0,0194 | 0,386 | 0,146 | |
| 16,3 | 13,9 | 0,0209 | 0,365 | 0,154 | |
| 15,8 | 14,0 | 0,0196 | 0,382 | 0,147 | |
| 9,0 | 12,0 | 0,0064 | 0,571 | 0,044 | |
| 16,0 | 14,0 | 0,0201 | 0,373 | 0,150 | |
| 11,5 | 12,8 | 0,0104 | 0,476 | 0,074 | |
| 16,1 | 14,6 | 0,0204 | 0,391 | 0,158 | |
| 13,2 | 14,1 | 0,0137 | 0,459 | 0,105 | |
| 13,9 | 13,9 | 0,0152 | 0,429 | 0,115 | |
| 14,4 | 13,8 | 0,0163 | 0,412 | 0,122 | |
| 7,3 | 12,3 | 0,0042 | 0,721 | 0,030 | |
| 13,2 | 13,5 | 0,0137 | 0,438 | 0,101 | |
| 14,7 | 13,6 | 0,0170 | 0,399 | 0,125 | |
| 11,9 | 14,3 | 0,0111 | 0,515 | 0,088 | |
| 7,7 | 11,6 | 0,0047 | 0,648 | 0,032 | |
| 10,0 | 13,0 | 0,0079 | 0,558 | 0,058 | |
| 12,4 | 13,3 | 0,0121 | 0,459 | 0,089 | |
| 13,2 | 15,1 | 0,0137 | 0,489 | 0,112 | |
| 13,2 | 14,0 | 0,0137 | 0,455 | 0,105 | |
| 11,8 | 13,3 | 0,0109 | 0,485 | 0,081 | |
| 9,1 | 12,1 | 0,0065 | 0,571 | 0,045 | |
| 8,8 | 12,3 | 0,0061 | 0,601 | 0,043 | |
| 11,0 | 12,5 | 0,0095 | 0,489 | 0,067 | |
| 15,2 | 14,9 | 0,0181 | 0,421 | 0,145 | |
| 11,1 | 12,8 | 0,0097 | 0,494 | 0,069 | |
| 14,0 | 14,1 | 0,0154 | 0,433 | 0,118 | |
| 10,8 | 13,9 | 0,0092 | 0,554 | 0,071 | |
| 11,1 | 14,3 | 0,0097 | 0,554 | 0,077 | |
| 10,2 | 11,4 | 0,0082 | 0,481 | 0,053 | |
| 11,4 | 13,5 | 0,0102 | 0,506 | 0,077 | |
| 11,2 | 11,1 | 0,0099 | 0,425 | 0,062 | |
| 15,1 | 13,5 | 0,0179 | 0,382 | 0,130 | |
| 8,5 | 10,9 | 0,0057 | 0,549 | 0,036 | |
| 12,8 | 14,4 | 0,0129 | 0,481 | 0,101 | |
| 13,3 | 13,7 | 0,0139 | 0,442 | 0,104 | |
| 12,5 | 13,0 | 0,0123 | 0,446 | 0,088 | |
| 10,2 | 11,5 | 0,0082 | 0,485 | 0,054 | |
| 10,2 | 12,2 | 0,0082 | 0,515 | 0,057 | |
| 15,0 | 14,0 | 0,0177 | 0,399 | 0,133 | |
| 10,5 | 14,2 | 0,0087 | 0,579 | 0,069 | |
| 13,0 | 14,0 | 0,0133 | 0,464 | 0,102 | |
| 12,1 | 13,7 | 0,0115 | 0,502 | 0,087 | |
| 14,3 | 13,5 | 0,0161 | 0,403 | 0,118 | |
| 13,3 | 13,1 | 0,0139 | 0,421 | 0,100 | |
| 8,7 | 10,0 | 0,0059 | 0,494 | 0,035 | |
| 10,4 | 11,5 | 0,0085 | 0,476 | 0,056 | |
| 16,1 | 13,3 | 0,0204 | 0,356 | 0,145 | |
| 7,1 | 12,0 | 0,0040 | 0,725 | 0,028 | |
| 11,5 | 10,5 | 0,0104 | 0,391 | 0,062 | |
| 12,0 | 13,9 | 0,0113 | 0,498 | 0,087 | |
| 14,3 | 14,1 | 0,0161 | 0,425 | 0,123 | |
| 10,5 | 14,0 | 0,0087 | 0,571 | 0,068 | |
| 13,8 | 14,1 | 0,0150 | 0,438 | 0,115 | |
| 9,0 | 12,1 | 0,0064 | 0,575 | 0,044 | |
| 15,4 | 13,9 | 0,0186 | 0,386 | 0,139 | |
| 8,0 | 10,5 | 0,0050 | 0,562 | 0,031 | |
| 17,7 | 13,4 | 0,0246 | 0,326 | 0,174 | |
| 12,8 | 13,9 | 0,0129 | 0,468 | 0,098 | |
| 10,6 | 12,2 | 0,0088 | 0,494 | 0,061 | |
| 12,5 | 12,8 | 0,0123 | 0,438 | 0,087 | |
| 8,9 | 10,3 | 0,0062 | 0,498 | 0,038 | |
| 10,2 | 12,5 | 0,0082 | 0,528 | 0,058 | |
| 16,3 | 13,5 | 0,0209 | 0,356 | 0,150 | |
| 10,8 | 13,3 | 0,0092 | 0,528 | 0,068 | |
| 9,8 | 12,1 | 0,0075 | 0,528 | 0,052 | |
| 10,9 | 12,4 | 0,0093 | 0,489 | 0,065 | |
| 13,0 | 12,5 | 0,0133 | 0,412 | 0,091 | |
| 8,5 | 11,2 | 0,0057 | 0,567 | 0,037 | |
| 13,2 | 14,2 | 0,0137 | 0,464 | 0,106 | |
| 14,5 | 14,1 | 0,0165 | 0,416 | 0,126 | |
| 10,0 | 13,0 | 0,0079 | 0,558 | 0,058 | |
| 11,8 | 12,0 | 0,0109 | 0,438 | 0,073 | |
| 10,7 | 12,4 | 0,0090 | 0,498 | 0,063 | |
| 14,1 | 13,6 | 0,0156 | 0,412 | 0,115 | |
| 10,3 | 13,0 | 0,0083 | 0,541 | 0,061 | |
| 11,2 | 13,3 | 0,0099 | 0,511 | 0,073 | |
| 12,0 | 14,2 | 0,0113 | 0,721 | 0,089 | |
| 7,6 | 10,2 | 0,0045 | 0,575 | 0,028 | |
| 15,7 | 14,0 | 0,0194 | 0,382 | 0,145 | |
| 11,9 | 14,5 | 0,0111 | 0,524 | 0,089 | |
| 14,0 | 14,4 | 0,0154 | 0,442 | 0,120 | |
| 14,9 | 15,3 | 0,0174 | 0,442 | 0,143 | |
| 8,6 | 13,1 | 0,0058 | 0,652 | 0,044 | |
| 16,1 | 14,4 | 0,0204 | 0,382 | 0,156 | |
| 15,9 | 14,2 | 0,0199 | 0,382 | 0,151 | |
| 11,8 | 13,6 | 0,0110 | 0,494 | 0,082 | |
| 14,6 | 15,1 | 0,0167 | 0,442 | 0,136 | |
| 11,6 | 13,9 | 0,0106 | 0,515 | 0,081 | |
| 12,6 | 13,8 | 0,0125 | 0,472 | 0,095 | |
| 18,7 | 16,1 | 0,0275 | 0,369 | 0,230 | |
| 12,1 | 14,6 | 0,0115 | 0,519 | 0,092 | |
| 11,3 | 14,4 | 0,0100 | 0,545 | 0,080 | |
| 11,2 | 14,1 | 0,0099 | 0,541 | 0,077 | |
| 12,5 | 14,4 | 0,0123 | 0,494 | 0,097 | |
| 15,1 | 15,2 | 0,0179 | 0,433 | 0,146 | |
| 11,5 | 13,1 | 0,0104 | 0,489 | 0,076 | |
| 14,8 | 14,7 | 0,0172 | 0,425 | 0,136 | |
| 13,0 | 12,3 | 0,0133 | 0,408 | 0,090 | |
| 10,4 | 13,2 | 0,0085 | 0,545 | 0,063 | |
| 14,6 | 13,7 | 0,0167 | 0,425 | 0,124 | |
| 14,7 | 13,5 | 0,0170 | 0,395 | 0,124 | |
| 12,5 | 13,5 | 0,0123 | 0,464 | 0,091 | |
| 14,3 | 14,2 | 0,0161 | 0,425 | 0,123 | |
| 8,7 | 12,1 | 0,0059 | 0,597 | 0,041 | |
| 12,8 | 13,7 | 0,0129 | 0,459 | 0,097 | |
| 14,3 | 13,8 | 0,0161 | 0,416 | 0,120 | |
| 11,7 | 12,5 | 0,0107 | 0,459 | 0,075 | |
| 13,4 | 13,0 | 0,0141 | 0,416 | 0,100 | |
| 11,3 | 13,1 | 0,0100 | 0,498 | 0,073 | |
| 14,2 | 14,5 | 0,0158 | 0,438 | 0,124 | |
| 12,4 | 14,3 | 0,0121 | 0,494 | 0,095 | |
| 13,9 | 14,8 | 0,0152 | 0,455 | 0,122 | |
| 13,2 | 13,5 | 0,0137 | 0,438 | 0,101 | |
| 13,5 | 13,6 | 0,0143 | 0,433 | 0,106 | |
| 13,5 | 13,5 | 0,0143 | 0,429 | 0,106 | |
| 14,5 | 13,0 | 0,0165 | 0,386 | 0,116 | |
| 10,8 | 12,5 | 0,0092 | 0,498 | 0,064 | |
| 9,4 | 12,3 | 0,0069 | 0,562 | 0,049 | |
| 17,7 | 14,0 | 0,0246 | 0,339 | 0,181 | |
| 12,1 | 12,8 | 0,0115 | 0,455 | 0,082 | |
| 12,0 | 14,3 | 0,0113 | 0,511 | 0,089 | |
| 15,3 | 15,3 | 0,0184 | 0,429 | 0,150 | |
| 13,7 | 14,5 | 0,0147 | 0,455 | 0,116 | |
| 16,8 | 15,0 | 0,0222 | 0,382 | 0,176 | |
| 15,4 | 13,8 | 0,0186 | 0,386 | 0,138 | |
| 8,2 | 12,6 | 0,0053 | 0,661 | 0,038 | |
| 10,6 | 13,8 | 0,0088 | 0,558 | 0,068 | |
| 10,2 | 13,5 | 0,0082 | 0,567 | 0,062 | |
| 13,5 | 14,8 | 0,0143 | 0,472 | 0,115 | |
| 9,6 | 12,3 | 0,0072 | 0,549 | 0,051 | |
| 9,2 | 13,0 | 0,0066 | 0,605 | 0,049 | |
| 9,4 | 13,6 | 0,0069 | 0,622 | 0,053 | |
| 9,0 | 12,2 | 0,0064 | 0,584 | 0,045 | |
| 10,8 | 13,5 | 0,0083 | 0,562 | 0,063 | |
| 9,2 | 13,0 | 0,0066 | 0,605 | 0,049 | |
| 11,8 | 12,0 | 0,0109 | 0,438 | 0,073 | |
| 10,7 | 13,5 | 0,0090 | 0,541 | 0,068 | |
| 15,9 | 15,2 | 0,0199 | 0,412 | 0,161 | |
| 11,0 | 14,6 | 0,0095 | 0,571 | 0,077 | |
| 9,6 | 13,6 | 0,0072 | 0,609 | 0,056 | |
| 10,2 | 13,0 | 0,0082 | 0,545 | 0,060 | |
| 11,0 | 13,0 | 0,0095 | 0,506 | 0,069 | |
| 15,2 | 13,7 | 0,0181 | 0,386 | 0,134 | |
| 9,2 | 10,5 | 0,0066 | 0,489 | 0,041 | |
| 12,5 | 13,3 | 0,0123 | 0,455 | 0,090 | |
| 9,4 | 12,6 | 0,0069 | 0,575 | 0,050 | |
| 10,8 | 13,8 | 0,0092 | 0,549 | 0,071 | |
| 11,3 | 14,0 | 0,0100 | 0,532 | 0,078 | |
| 14,3 | 13,5 | 0,0161 | 0,403 | 0,118 | |
| 11,0 | 12,3 | 0,0095 | 0,481 | 0,066 | |
| 9,0 | 12,0 | 0,0064 | 0,571 | 0,044 | |
| 8,2 | 12,4 | 0,0053 | 0,648 | 0,038 | |
| 11,0 | 13,0 | 0,0095 | 0,506 | 0,069 | |
| 15,8 | 13,8 | 0,0196 | 0,373 | 0,145 | |
| 11,4 | 14,2 | 0,0102 | 0,536 | 0,080 | |
| 12,5 | 13,7 | 0,0123 | 0,472 | 0,093 | |
| 10,2 | 13,2 | 0,0082 | 0,554 | 0,061 | |
| 13,8 | 14,3 | 0,0150 | 0,446 | 0,116 | |
| 12,9 | 13,7 | 0,0131 | 0,455 | 0,098 | |
| 15,8 | 13,9 | 0,0196 | 0,378 | 0,146 | |
| 12,2 | 13,6 | 0,0117 | 0,476 | 0,088 | |
| 11,7 | 12,5 | 0,0127 | 0,459 | 0,075 | |
| 12,6 | 13,8 | 0,0125 | 0,472 | 0,095 | |
| 17,0 | 14,1 | 0,0227 | 0,356 | 0,169 | |
| 11,9 | 13,5 | 0,0111 | 0,485 | 0,083 | |
| 13,4 | 14,6 | 0,0141 | 0,468 | 0,112 | |
| 19,5 | 15,3 | 0,0299 | 0,335 | 0,237 | |
| 13,0 | 15,5 | 0,0133 | 0,511 | 0,112 | |
| 18,3 | 15,0 | 0,0263 | 0,352 | 0,206 | |
| 12,8 | 13,0 | 0,0119 | 0,455 | 0,085 | |
| 14,4 | 13,6 | 0,0163 | 0,403 | 0,120 | |
| 17,6 | 14,1 | 0,0243 | 0,343 | 0,181 | |
| 13,0 | 13,9 | 0,0133 | 0,459 | 0,101 | |
| 10,9 | 13,1 | 0,0093 | 0,515 | 0,068 | |
| 11,1 | 12,5 | 0,0097 | 0,485 | 0,068 | |
| 11,3 | 13,5 | 0,0100 | 0,511 | 0,075 | |
| 10,3 | 12,9 | 0,0083 | 0,536 | 0,061 | |
| 12,5 | 13,7 | 0,0123 | 0,472 | 0,093 | |
| 11,1 | 13,0 | 0,0097 | 0,502 | 0,070 | |
| 10,1 | 13,0 | 0,0080 | 0,554 | 0,059 | |
| 15,8 | 12,1 | 0,0196 | 0,330 | 0,128 | |
| 15,2 | 13,5 | 0,0181 | 0,382 | 0,132 |
Литература
|
|
|
|
|
|
|
|
|
1. Степин В.В. Применение математической статистики в лесном хозяйстве. М. – 1970
2. Трулль О.А. Математическая статистика в лесном хозяйстве, Минск, «Высшая школа», 1966
3. Алексеев А.С. Математические методы и модели в лесном хозяйстве, Учебное пособие, Л.: ЛТА, 1988
4. Кравченко Г.Л. Математические методы и модели в вариационной статистике. Методические указания по выполнению лабораторных работ для студентов специальности 1512 «Лесное хозяйство». – БТИ. 1991
Содержание
Введение. 5
Практическая работа. Получение индивидуального задания. 6
Исходные данные. 7
Расчет средних показателей. 8
Лабораторная работа. Группировка выборочной совокупности. 9
Практическая работа. Расчет статистических характеристик большой выборочной совокупности 13
Расчет статистических характеристик большой выборочной совокупности через центральное отклонение 13
Лабораторная работа. Расчет статистических характеристик большой выборочной совокупности через моменты.. 15
Расчет моментов. 15
Расчет центральных и основных моментов. 16
Практическая работа. Расчет статистических характеристик при помощи моментов. 17
Лабораторная работа. Теоретическое распределение. 19
Расчет частот нормального распределения. 19
Расчет теоретических частот распределения типа А.. 21
Расчет теоретических частот по распределению типа В.. 24
Практическая работа. Расчет критерия согласия Пирсона. 26
КОРРЕЛЯЦИОННЫЙ АНАЛИЗ. 28
Лабораторная работа. Корреляция малой выборочной совокупности. 28
Расчет показателей малой выборочной совокупности. 29
Практическая работа. Расчет характеристик связи между показателями. 30
Получение уравнения регрессии по данным взаимосвязи. 31
Графическое отражение взаимосвязи. 31
Лабораторная работа. Корреляция большой выборочной совокупности. 32
Лабораторная работа. Расчет статистических характеристик Статистические характеристики по ряду х 37
Статистические характеристики по ряду у. 37
Характеристики связи большой выборочной совокупности. 38
Построение графика корреляции. 39
Практическая работа. ДИСПЕРСИОННЫЙ АНАЛИЗ. 41
Лабораторная работа. РЕГРЕССИОННЫЙ АНАЛИЗ. 44
Метод избранных координат точек. 44
Проверка адекватности уравнения. 44
Метод статистических характеристик. 45
Лабораторная работа. Метод наименьших квадратов. 46
Приложения. 49
Литература. 56
А.А. Соломников
|
|
|


