 |
Г. В. Красоленко, Н. В. Сванидзе, Г. В. Якунина
|
|
|
|
Министерство образования и науки Российской Федерации
Санкт-Петербургский государственный
архитектурно-строительный университет
Факультет городского строительства и жилищно-коммунального хозяйства
Кафедра математики
Г. В. КРАСОЛЕНКО, Н. В. СВАНИДЗЕ, Г. В. ЯКУНИНА
Дифференциальное и интегральное
исчисление в случае функции одной
переменной
Рабочая программа, методические указания и
контрольные задания
Санкт-Петербург
УДК 517. 22 + 517. 968+519. 95 (075. 8)
Рецензент канд. физ. -мат. наук, доцент Е. К. Ершов (СПбГАСУ)
Дифференциальное и интегральное исчисление в случае функции одной переменной: рабочая программа, методические указания и контрольные задания / сост.: Г. В. Красоленко, Н. В. Сванидзе, Г. В. Якунина; СПбГАСУ. – СПб., 2012. –48 с
Даются методические рекомендации по выполнению индивидуального домашнего задания (третьей и четвертой контрольных работ) по курсу высшей математики: «Дифференциальное и интегральное исчисление в случае функции одной переменной » и предназначены для студентов факультета безотрывной формы обучения.
Приводятся варианты контрольных работ.
Ил. 5. Библиогр.: 9 назв.
Ó Санкт-Петербургский государственный
архитектурно-строительный университет, 2012
ВВЕДЕНИЕ
Прежде чем приступать к выполнению контрольных работ, Вам необходимо ознакомиться с «Рабочей программой» и изучить соответствующий теоретический материал по учебникам, указанным в разделе «Рекомендуемая литература».
Во время экзаменационной сессии для студентов безотрывной формы обучения читают установочные лекции и проводят практические занятия, которые носят обзорный характер.
|
|
|
К сдаче экзамена или зачета допускаются студенты, контрольные работы которых проверены и зачтены преподавателями кафедры математики.
Обратите внимание на оформление контрольной работы. На титульном листе должны быть указаны:
фамилия, имя, отчество
Номер студенческого билета (или зачетной книжки)
Специальность
Название дисциплины и номер контрольной работы
Номер варианта
Номер варианта, который должен выполнять студент, соответствует последней цифре номера студенческого билета (или зачетной книжки). Цифре ноль соответствует вариант № 10
РАБОЧАЯ ПРОГРАММА КУРСА ВЫСШЕЙ МАТЕМАТИКИ
Дифференциальное исчисление в случае функции одной переменной
1. Геометрическая и механические задачи, приводящие к понятию производной (задача о построении касательной к кривой и задача о вычислении скорости материальной точки).
2. Производная функции. Её геометрическая и механическая трактовки.
3. Непрерывность функции, имеющей производную. Необходимое условие существования производной и его недостаточность.
4. Основные правила нахождения производных (суммы и произведения нескольких функций, частного двух функций, сложной функции, обратной функции). Производная постоянной. Производные основных элементарных функций. Таблица производных. Производная неявно заданной функции и функции, заданной в параметрической форме.
5. Касательная и нормаль к плоской кривой и их уравнения.
6. Производные высших порядков. Механическая трактовка второй производной.
7. Теоремы о средних значениях дифференцируемых функций (теоремы Ферма, Ролля, Лагранжа, Коши).
8. Основные виды неопределённостей. Раскрытие неопределённостей вида 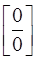 и
и  с помощью правила Лопиталя.
с помощью правила Лопиталя.
|
|
|
9. Возрастание и убывание функции. Необходимые и достаточные условия возрастания, убывания и постоянства функции.
10. Экстремум функции (локальный максимум и локальный минимум). Необходимое условие существования экстремума дифференцируемой функции и его недостаточность. Острый экстремум. Два варианта достаточных условий существования экстремума дифференцируемой функции.
11. Наибольшее и наименьшее значения функции, непрерывной на замкнутом промежутке.
12. Выпуклость вверх и выпуклость вниз плоской кривой. Необходимые и достаточные условия выпуклости вверх и выпуклости вниз плоской кривой. Точки перегиба. Необходимое условие существования точки перегиба дифференцируемой функции и его недостаточность. Достаточные условия существования точки перегиба кривой.
13. Асимптота кривой. Нахождение вертикальных и наклонных асимптот.
14. Исследование функций, заданных в явной аналитической форме, и построение их графиков.
15. Дифференциал функции. Дифференциал как главная линейная часть приращения функции. Геометрическая трактовка дифференциала функции. Основные правила вычисления дифференциалов суммы и произведения нескольких функций, частного двух функций, сложной функции. Дифференциал постоянной функции. Инвариантность формы дифференциала функции.
16. Приближённые вычисления с помощью дифференциалов.
17. Понятие о длине дуги плоской кривой. Дифференциал длины дуги плоской кривой, его выражение в декартовой и полярной системах координат.
18. Кривизна плоской кривой. Вычисление кривизны плоской кривой в декартовой системе координат.
19. Окружность кривизны, ее центр и радиус. Выражение радиуса кривизны и координат центра кривизны в декартовой системе координат. Эволюта плоской кривой и ее свойства.
20. Понятие вектор – функции скалярного аргумента. Годограф вектор – функции скалярного аргумента.
21. Уравнения пространственной кривой в векторно-параметрической и параметрической формах. Винтовая линия и ее параметрические уравнения.
22. Предел, приращение, производная и дифференциал вектор – функции скалярного аргумента. Орт касательной к годографу. Основные правила дифференцирования вектор – функции скалярного аргумента.
|
|
|
23. Уравнение касательной к пространственной кривой.
24. Вторая производная вектор – функции скалярного аргумента. Соприкасающаяся плоскость. Главная нормаль к годографу и ее орт. Кривизна годографа. Выражение кривизны годографа через первую и вторую производные вектор–функции скалярного аргумента.
|
|
|


