 |
Интегральное исчисление в случае функции одной переменной. Формулы Тейлора и Маклорена. Гиперболические функции
|
|
|
|
Интегральное исчисление в случае функции одной переменной. Формулы Тейлора и Маклорена. Гиперболические функции
1. Понятие о первообразной функции и неопределенном интеграле.
2. Основные свойства неопределенного интеграла.
3. Таблица неопределенных интегралов.
4. Интегрирование методом замены переменной.
5. Интегрирование по частям.
6. Интегралы от некоторых функций, содержащих квадратный трехчлен в знаменателе.
7. Простейшие рациональные дроби и их интегрирование.
8. Разложение правильной рациональной дроби в сумму простейших дробей.
9. Интегрирование рациональных дробей.
10. Интегралы от произведения синуса и косинуса различных аргументов.
11. Интегралы от произведения степеней синуса и косинуса одного аргумента.
12. Вычисление интегралов от иррациональных функций вида 
13. Вычисление интегралов от иррациональных функций вида 
с помощью тригонометрических подстановок Эйлера.
14. О функциях, интегралы от которых не выражаются через элементарные функции.
15. Геометрическая задача, приводящая к понятию об определенном интеграле. Определенный интеграл от непрерывной функции по конечному промежутку как предел интегральной суммы Римана. Геометрическая трактовка определенного интеграла.
16. Основные свойства определенного интеграла.
17. Теорема Барроу. Дифференцирование определенного интеграла по параметру, от которого зависят пределы интегрирования.
18. Формула Ньютона-Лейбница.
19. Замена переменной и интегрирование по частям в определенном интеграле.
20. Теорема о среднем значении.
21. Формулы Тейлора и Маклорена. Выражение остаточного члена формул Тейлора и Маклорена в форме Лагранжа.
|
|
|
22. Гиперболические функции вещественного аргумента и их свойства.
23. Несобственные интегралы.
24. Вычисление площадей плоских фигур.
25. Вычисление объемов тел вращения.
26. Вычисление длин дуг плоских кривых.
27. Вычисление площадей поверхностей вращения.
Примерный вариант контрольной работы № 3
по дифференциальному исчислению в случае функции одной переменной
1. Найти производную по правилам и формулам дифференцирования
а) 
б)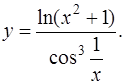 
2. Функция 
задана в параметрической форме
Найти параметрическую форму её производной 
3. Показать, что функция 
является решением дифференциального уравнения 
4. Написать уравнение касательной к параболе 
в точке ее пересечения с осью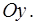 
Построить параболу и ее касательную в декартовой системе координат.
5. Тело движется прямолинейно по закону 
где 
измеряется в секундах, а 
– в метрах. Определить скорость и ускорение в момент времени 
с.
Решение задачи № 1
В этой задаче требуется найти производные функций, заданных явно.
В примере а) функция
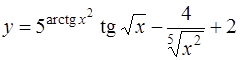
представляет собой сумму трех функций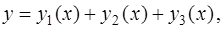 
где 
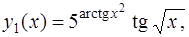
и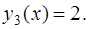 
По правилу дифференцирования суммы трех функций имеем 
Найдём производную функции 
Для этого сначала воспользуемся правилом дифференцирования произведения двух функций:
,
в результате получаем, что
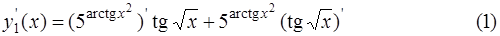
Для вычисления производных, входящих в это выражение воспользуемся теоремой о дифференцировании сложной функции.
Теорема (цепное правило). Пусть функция 
имеет в точке 
производную 
, а функция 
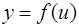имеет в точке 
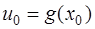производную 
Тогда сложная функция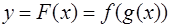 
имеет в точке производную
Функция 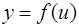называется внешней функцией, а –внутренней функцией. (Производная сложной функции равна произведению производной внешней функции на производную внутренней функции. )
|
|
|
В обозначениях Лейбница эта теорема формулируется более изящно:
Применим цепное правило для вычисления производной функции 
Для этого положим 
и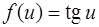 
. Тогда 
Так как 
и 
, то, имеем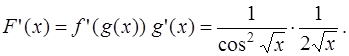 
В обозначениях Лейбница те же вычисления принимают вид
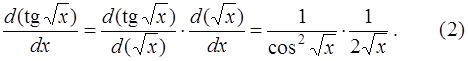
Здесь при вычислении производной 
с функцией 
обращаемся как с единым символом.
Конечно, цепное правило можно применять повторно. Вычисляя производную функции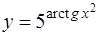 
, получаем
Подставляя вычисленные производные 
и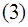 
в выражение 
имеем
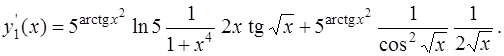
Для завершения решения примера а) осталось вычислить производные функций 
и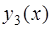 
:
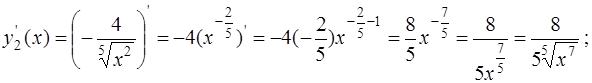
Окончательно получаем:
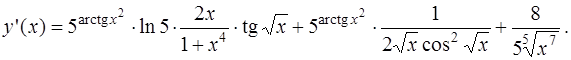
В примере б) функция 
представляет собой частное двух сложных функций. Применяя правило дифференцирования частного, получаем
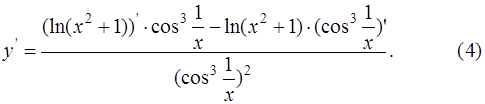
С помощью цепного правила вычислим производные функций, входящие в правую часть выражения (4):
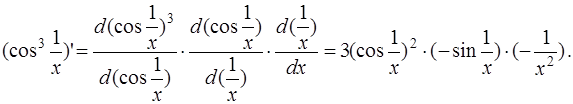
После подстановки этих производных в формулу (4), окончательно получаем
|
|
|
