 |
Решение примера б). Решение примера в). Решение задачи № 2. Сначала сделаем замену переменной Тогда
|
|
|
|
Решение примера б)
Для вычисления интеграла
воспользуемся теоремой о замене переменной и формулой интегрирования по частям.
Сначала сделаем замену переменной 
Тогда
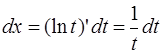
и интеграл приводится к виду
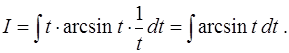
К этому результату можно прийти и другим способом. После выбора подстановки 
вычислим дифференциал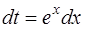 
и перегруппируем функции, стоящие в подынтегральном выражении, следующим образом:
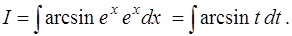
Для вычисления интеграла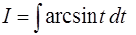 
применим формулу интегрирования по частям.
Пусть 
и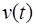 
– две непрерывно дифференцируемые функции на некотором промежутке. Тогда имеет место формула
которая называется формулой интегрирования по частям.
Напомним, что 
и 
В нашем случае положим
Тогда
Интеграл 
вычислим с помощью подстановки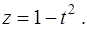 
Тогда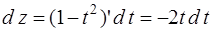 
, 
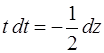и в результате получаем
Таким образом,
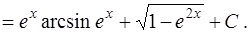
Ответ примера б): 
Решение примера в)
В этом примере используются методы интегрирования тригонометрических функций (см. [1], [2] и [6]).
Для вычисления интеграла 
применим следующие тригонометрические формулы
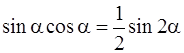и 
Тогда
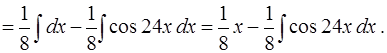
Последний интеграл 
вычислим с помощью замены переменной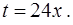 
Отсюда 
и 
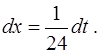В результате получаем
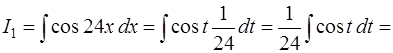
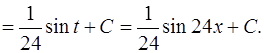
Ответ примера в):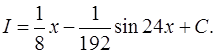 
Решение задачи № 2
В этой задаче нужно вычислить площадь фигуры, ограниченной линиями 
Построим заданную фигуру (см. рис. 3). Найдем точки пересечения указанных в условии линий (параболы и прямой). Решим для этого систему уравнений
Она равносильна системе
откуда 
Уравнение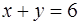 
задает прямую, которая проходит через две найденные точки c координатами 
и 
.
Уравнение параболы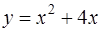 
приведём к каноническому виду, выделяя полный квадрат по переменной 
: 
|
|
|
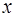Тогда каноническое уравнение параболы имеет вид
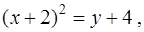
из которого видно, что парабола имеет осью симметрии вертикальную прямую 
, вершину в точке 
и ветви параболы направлены вверх (в направлении оси 
).
Для того, чтобы найти площадь построенной фигуры, рекомендуют сначала составить выражение бесконечно малого элемента искомой площади, а затем проинтегрировать полученный результат в пределах изменения аргумента (см. [7]).
Обозначим бесконечно малый элемент площади через 
.
Он равен площади прямоугольника, заштрихованного на рис. 3, со сторонами 
и 
, т. е.
Так как 
и 
, то
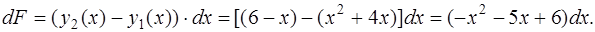
Искомую площадь получаем, проинтегрировав полученный результат в пределах изменения переменной 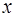от 
до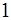 
.
Тогда
Решение задачи № 4
В данной задаче нужно вычислить объём тела, полученного вращением вокруг оси плоской фигуры, ограниченной параболой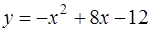 
и прямой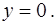 
Чтобы построить параболу, ее уравнение
(1)
приведём к каноническому виду, выделяя полный квадрат по переменной 
:
,
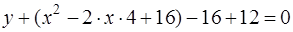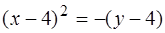. (2)
Следовательно, парабола имеет ось симметрии 
, вершину в точке 
. Ветви параболы направлены вниз (в направлении, противоположном положительному направлению оси ). Кривая пересекает ось 
в точках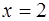 
и 
. Заданная фигура заштрихована на рис. 4 (а). Вращая её вокруг оси , получим тело с полостью.
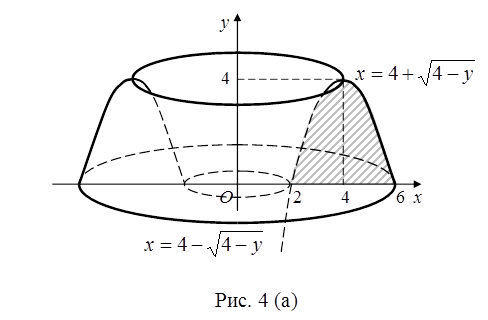
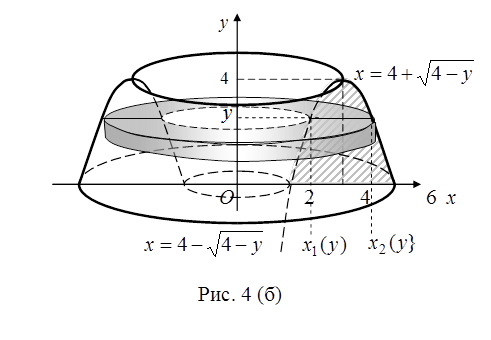
Найдем объем 
тела вращения. Для этого составим выражение бесконечно малого элемента объема 
, а затем проинтегрируем полученный результат в пределах изменения аргумента
(см. [7]).
Бесконечно малый элемент искомого объема равен объему кольцевого цилиндра с внешним радиусом 
, внутренним радиусом 
и высотой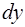 
(см. рис. 4 (б), на котором выделен затененный цилиндр):
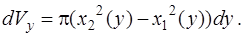(3)
Рассечём тело вращения плоскостью, перпендикулярной оси . В сечении получим кольцо (рис. 4 (б)), которое является основанием нашего бесконечно тонкого кольцевого цилиндра. Чтобы определить внутренний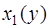 
и внешний 
радиусы этого кольца, вернемся к уравнению параболы. Из уравнения (2) найдём
|
|
|
,
следовательно,
Очевидно, что первая функция задает внешний радиус кольца, а вторая – внутренний, т. е.
и 
Найдём бесконечно малый элемент искомого объёма по формуле (3):
.
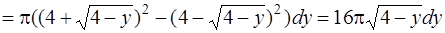Для вычисления объёма тела вращения проинтегрируем полученный результат по переменной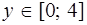 
. Тогда
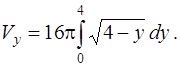
Для вычисления интеграла сделаем подстановку 
и используем теорему о замене переменной.
Найдем пределы интегрирования по переменной 
: если 
, то 
если 
, то 
Так как 
то 
и в результате получаем
|
|
|
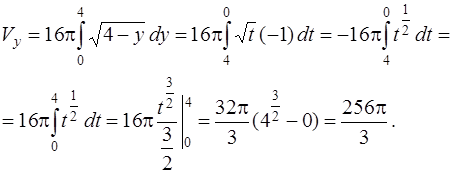
