 |
Контрольная работа № 4. по интегральному исчислению функции одной переменной. Рекомендуемая литература
|
|
|
|
Контрольная работа № 4
по интегральному исчислению функции одной переменной
Вариант I
1. Вычислить следующие интегралы:
а) 
б)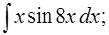 
в) 
2. Вычислить площадь фигуры, ограниченной линиями
и 
3. Вычислить объем тела, образованного вращением вокруг оси 
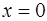фигуры, ограниченной линиями 
, 
и 
4. Вычислить несобственный интеграл (или доказать его расходимость) 
Вариант 2
1. Вычислить следующие интегралы:
а) 
б)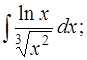 
в) 
2. Вычислить площадь фигуры, ограниченной линиями
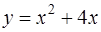и 
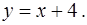
3. Вычислить объем тела, образованного вращением вокруг оси 
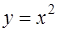фигуры, ограниченной линиями 
и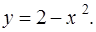 
4. Вычислить несобственный интеграл (или доказать его расходимость)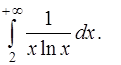 
Вариант 3
1. Вычислить следующие интегралы:
а)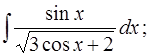 
б) 
в)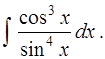 
2. Вычислить площадь фигуры, ограниченной линиями
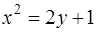и 
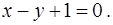
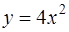3. Вычислить объем тела, образованного вращением вокруг оси фигуры, ограниченной линиями 
и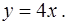 
4. Вычислить несобственный интеграл (или доказать его расходимость)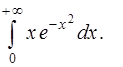 
Вариант 4
1. Вычислить следующие интегралы:
а)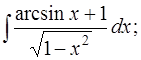 
б)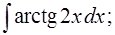 
в)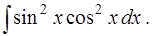 
2. Вычислить площадь фигуры, ограниченной линиями
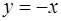и 
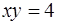3. Вычислить объем тела, образованного вращением вокруг оси фигуры, ограниченной линиями 
, 
и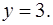 
4. Вычислить несобственный интеграл (или доказать его расходимость) 
|
|
|
Вариант 5
1. Вычислить следующие интегралы:
а) 
б) 
в)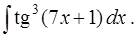 
2. Вычислить площадь фигуры, ограниченной линиями
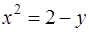и 
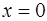3. Вычислить объем тела, образованного вращением вокруг оси фигуры, ограниченной линиями 
, 
, и 
4. Вычислить несобственный интеграл (или доказать его расходимость) 
Вариант 6
1. Вычислить следующие интегралы:
а) 
б) 
в) 
2. Вычислить площадь фигуры, ограниченной линиями
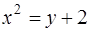и
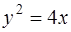3. Вычислить объем тела, образованного вращением вокруг оси фигуры, ограниченной линиями 
и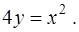 
4. Вычислить несобственный интеграл (или доказать его расходимость) 
Вариант 7
1. Вычислить следующие интегралы:
а) 
б) 
в)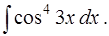 
2. Вычислить площадь фигуры, ограниченной линиями
и 
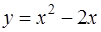3. Вычислить объем тела, образованного вращением вокруг оси фигуры, ограниченной линиями 
и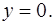 
4. Вычислить несобственный интеграл (или доказать его расходимость) 
Вариант 8
1. Вычислить следующие интегралы:
а)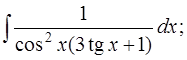 
б) 
в) 
2. Вычислить площадь фигуры, ограниченной линиями
и 
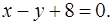
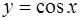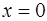3. Вычислить объем тела, образованного вращением вокруг оси фигуры, ограниченной линиями 
, 
, и 
|
|
|
4. Вычислить несобственный интеграл (или доказать его расходимость) 
Вариант 9
1. Вычислить следующие интегралы:
а) 
б)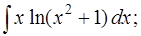 
в) 
2. Вычислить площадь фигуры, ограниченной линиями
и 
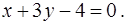
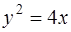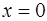3. Вычислить объем тела, образованного вращением вокруг оси фигуры, ограниченной линиями , и 
4. Вычислить несобственный интеграл (или доказать его расходимость)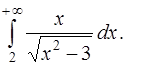 
Вариант 10
1. Вычислить следующие интегралы:
а)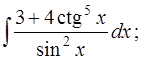 
б) 
в)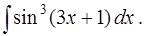 
2. Вычислить площадь фигуры, ограниченной линиями
и 
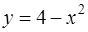3. Вычислить объем тела, образованного вращением вокруг оси фигуры, ограниченной линиями 
и 
4. Вычислить несобственный интеграл (или доказать его расходимость) 
Рекомендуемая литература
1. Натансон, И. П. Краткий курс высшей математики / И. П. Натансон. – СПб. : Лань, 2005.
2. Пискунов, Н. С. Дифференциальное и интегральное исчисление / Н. С. Пискунов. – СПб. : Мифрил, Физматгиз, 1996.
3. Берс, Л. Математический анализ. / Липман Берс. –М. : Высшая школа, 1975.
4. Нумеров, С. Н. Определенный интеграл: методические указания к выполнению задания для студентов всех специальностей ЛИСИ / С. Н. Нумеров. – Л. : ЛИСИ, 1984.
5. Ивочкина, Н. М. Дифференциальное исчисление в случае функции одного аргумента: Учебное пособие для студентов строительных вузов / Н. М. Ивочкина., Л. Б. Клебанов. – СПб. : СПбГАСУ, 1993.
6. Смирнова, В. Б. Неопределенный интеграл: Учебное пособие для студентов всех специальностей и всех форм обучения / В. Б. Смирнова., Л. Е. Морозова. – СПб. : СПбГАСУ, 2010.
7. Морозова, Л. Е. Определенный интеграл: Учебное пособие для студентов всех специальностей и всех форм обучения / Л. Е. Морозова., В. Б. Смирнова. – СПб. : СПбГАСУ, 2011.
8. Берман, Г. Н. Сборник задач по курсу математического анализа / Г. Н. Берман. – М. : Наука, 1985.
9. Демидович, Б. П. Задачи и упражнения по математическому анализу / Б. П. Демидович. – М. : Физматгиз, 1962.
|
|
|
|
|
|
