 |
Решение задачи № 2. Для этого воспользуемся формулой . которая позволяет вычислить значение производной от функции, заданной в параметрической форме, не находя непосредственной зависимости от
|
|
|
|
Решение задачи № 2
В этой задаче требуется найти производную функции 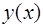 , заданную параметрическими уравнениями:
, заданную параметрическими уравнениями:

Для этого воспользуемся формулой

которая позволяет вычислить значение производной  от функции, заданной в параметрической форме, не находя непосредственной зависимости
от функции, заданной в параметрической форме, не находя непосредственной зависимости 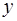 от
от 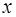 .
.
Вычислим производные  и
и 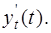
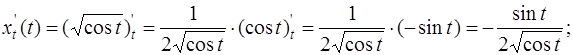

Следовательно,

Обращаем Ваше внимание, что производная  от функции, заданной в параметрической форме, также оказывается функцией, заданной в параметрической форме:
от функции, заданной в параметрической форме, также оказывается функцией, заданной в параметрической форме:
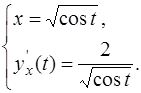
Замечание. Пусть параметр  меняется в интервале:
меняется в интервале:  Тогда переменная
Тогда переменная 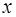 меняется в интервале:
меняется в интервале:  и (в нашем случае, исключая параметр
и (в нашем случае, исключая параметр  из параметрических уравнений) можно получить явное задание функции
из параметрических уравнений) можно получить явное задание функции  и ее производной
и ее производной 
Решение задачи № 3
В этой задаче требуется показать, что функция  является решением дифференциального уравнения второго порядка
является решением дифференциального уравнения второго порядка 
Для этого нужно найти её первую и вторую производные, подставить их в левую часть уравнения и убедиться в справедливости полученного равенства.
Используя цепное правило, вычислим предварительно производные следующих сложных функций:
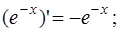
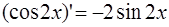 и
и 
Тогда


Вычислим вторую производную. По определению вторая производная есть первая производная от первой производной.


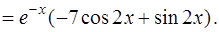
Подставим теперь функцию  и найденные ее производные в левую часть уравнения:
и найденные ее производные в левую часть уравнения:


( вынесем общий множитель  и сгруппируем слагаемые, содержащие функции
и сгруппируем слагаемые, содержащие функции 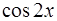 и
и  )
)

Равенство нулю значения левой части уравнения показывает, что функция  является решением дифференциального уравнения второго порядка
является решением дифференциального уравнения второго порядка 
Решение задачи № 4
|
|
|
Напомним одно из определений производной и ее геометрический смысл.
Определение. Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки 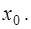 Функция имеет производную
Функция имеет производную 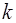 в точке
в точке 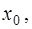 если она допускает следующее представление
если она допускает следующее представление

где 
или, что то же самое,
 непрерывна в точке
непрерывна в точке 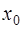 и
и 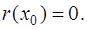
График линейной функции
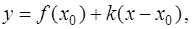 где
где 
есть прямая, которая называется касательной к графику функции  в точке
в точке 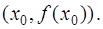
Если касательная составляет угол  с положительным направлением оси
с положительным направлением оси 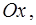 то число
то число 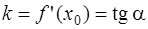 называется угловым коэффициентом (или наклоном) касательной (см. рис. 1).
называется угловым коэффициентом (или наклоном) касательной (см. рис. 1).
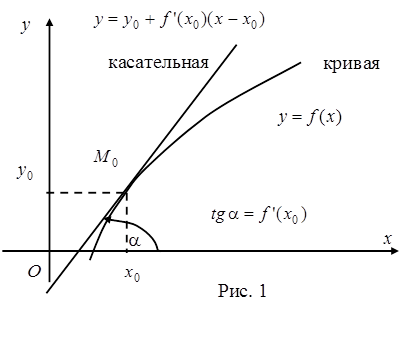
Число же
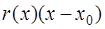
указывает ошибку, которую мы допускаем, если при вычислении значения 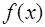 в точках
в точках 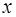 , близких к
, близких к 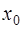 , заменяем график функции
, заменяем график функции  её касательной в точке
её касательной в точке 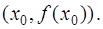
Приступим к решению нашей задачи. Для этого найдем координаты точки касания 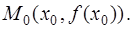 Так как
Так как  одновременно является точкой пересечения параболы с осью
одновременно является точкой пересечения параболы с осью 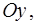 то абсцисса
то абсцисса 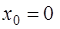 и, следовательно, ордината точки касания
и, следовательно, ордината точки касания
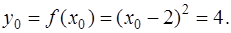
Найдем угловой коэффициент касательной  Для этого вычислим производную
Для этого вычислим производную  и найдем ее значение в точке
и найдем ее значение в точке 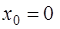 , таким образом,
, таким образом,

Уравнение касательной к параболе в точке  с угловым коэффициентом
с угловым коэффициентом  будет иметь вид
будет иметь вид
 или
или 
Осталось построить параболу  и ее касательную
и ее касательную  в декартовой системе координат.
в декартовой системе координат.
Прямую  строим по двум точкам
строим по двум точкам  и
и  (см. рис. 2).
(см. рис. 2).
Парабола  имеет вершину в точке
имеет вершину в точке 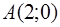 и ее ветви направлены вверх. Прямая
и ее ветви направлены вверх. Прямая  является осью симметрии параболы.
является осью симметрии параболы.
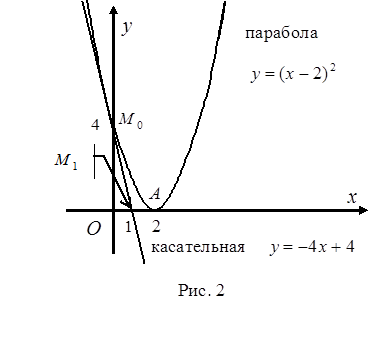 Решение задачи № 5
Решение задачи № 5
Условимся, что при решении задач, использующих размерные величины, будем применять основные единицы измерения международной системы СИ.
Напомним механический смысл первой и второй производных.
Рассмотрим частицу, движущуюся вдоль прямой (прямолинейное движение). Под частицей понимается тело, размерами которого можно пренебречь, так что его можно считать математической точкой. Выберем на прямой, по которой движется наша точка, точку  и положительное направление. Длину будем измерять в метрах, а время в секундах. Выберем, далее, момент времени, начиная с которого отсчитывается время.
и положительное направление. Длину будем измерять в метрах, а время в секундах. Выберем, далее, момент времени, начиная с которого отсчитывается время.
|
|
|
Таким образом, предполагаем, что частица движется вдоль числовой прямой и это движение описывается функцией  сопоставляющей каждому моменту времени
сопоставляющей каждому моменту времени  координату
координату  частицы в этот момент.
частицы в этот момент.
Тогда
скорость  частицы есть первая производная пути по времени:
частицы есть первая производная пути по времени: 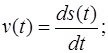
|
|
|


