 |
Решение задачи № 4. Контрольная работа № 3. по дифференциальному исчислению функций одной переменной
|
|
|
|
Решение задачи № 4
В этой задаче требуется исследовать интеграл 
Данный интеграл является несобственным, так как промежуток интегрирования 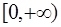 бесконечный. Напомним определение несобственного интеграла по бесконечному промежутку.
бесконечный. Напомним определение несобственного интеграла по бесконечному промежутку.
Пусть функция 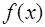 определена при всех
определена при всех  и интегрируема на каждом конечном промежутке
и интегрируема на каждом конечном промежутке 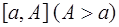 . Рассмотрим предел
. Рассмотрим предел
 (1)
(1)
Его называют несобственным интегралом по бесконечному промежутку и обозначают символом
 . (2)
. (2)
Таким образом,

Если предел (1) существует и конечен, то говорят, что интеграл (2) существует или сходится. Если же рассматриваемый предел (1) не существует или бесконечен, то говорят, что несобственный интеграл (2) не существует или расходится.
В нашем случае


Для вычисления интеграла используем теорему о замене переменной в определенном интеграле, сделав подстановку 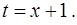
Найдем пределы интегрирования по переменной  : если
: если 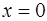 , то
, то  если
если 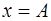 , то
, то 
Так как 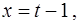 то
то  и в результате получаем
и в результате получаем
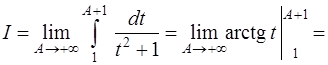

Следовательно, данный интеграл сходится и равен 
Контрольная работа № 3
по дифференциальному исчислению функций одной переменной
Вариант № 1
1. Найти производную по правилам и формулам дифференцирования
а) 
б) 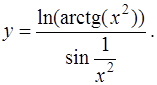
2. Функция  задана в параметрической форме
задана в параметрической форме

Найти параметрическою форму её производной 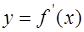 :
:
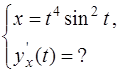
3. Показать, что функция  является решением дифференциального уравнения
является решением дифференциального уравнения 
4. Найти уравнения касательных к кривой 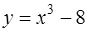 в точках пересечения её с осями координат. Построить кривую и касательные в декартовой системе координат.
в точках пересечения её с осями координат. Построить кривую и касательные в декартовой системе координат.
|
|
|
5. Тело движется прямолинейно по закону 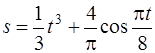 , где
, где  измеряется в секундах, а
измеряется в секундах, а  – в метрах. Определить скорость и ускорение тела в момент времени
– в метрах. Определить скорость и ускорение тела в момент времени 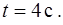
Вариант № 2
1. Найти производную по правилам и формулам дифференцирования
а) 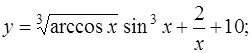
б) 
2. Функция  задана в параметрической форме
задана в параметрической форме
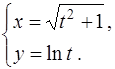
Найти параметрическою форму её производной 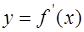 :
:

3. Показать, что функция  является решением дифференциального уравнения
является решением дифференциального уравнения 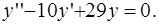
4. Найти уравнения касательных к кривой 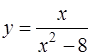 в точках, ордината которых
в точках, ордината которых  Построить эти касательные в декартовой системе координат.
Построить эти касательные в декартовой системе координат.
5. Тело движется прямолинейно по закону 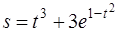 , где
, где  измеряется в секундах, а
измеряется в секундах, а  – в метрах. Определить скорость и ускорение тела в момент времени
– в метрах. Определить скорость и ускорение тела в момент времени 
Вариант № 3
1. Найти производную по правилам и формулам дифференцирования
а) 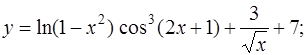
б) 
2. Функция  задана в параметрической форме
задана в параметрической форме

Найти параметрическою форму её производной 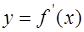 :
:

3. Найти  , если
, если 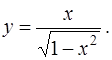
4. В каких точках кривой 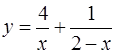 касательная параллельна оси
касательная параллельна оси 
5. Закон движения материальной точки имеет вид  , где
, где  измеряется в секундах, а
измеряется в секундах, а  – в метрах. Определить скорость и ускорение материальной точки в момент времени
– в метрах. Определить скорость и ускорение материальной точки в момент времени 
Вариант № 4
1. Найти производную по правилам и формулам дифференцирования
а) 
б) 
2. Функция  задана в параметрической форме
задана в параметрической форме

Найти параметрическою форму её производной 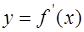 :
:

3. Показать, что функция 
 удовлетворяет уравнению
удовлетворяет уравнению 
4. Найти уравнения касательных к графику функции 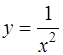 в точках, ордината которых
в точках, ордината которых  . Построить график функции и касательные в декартовой системе координат.
. Построить график функции и касательные в декартовой системе координат.
5. По параболе  движется точка так, что ее абсцисса изменяется в зависимости от времени
движется точка так, что ее абсцисса изменяется в зависимости от времени  по закону
по закону 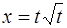 , где
, где  измеряется в секундах, а
измеряется в секундах, а 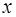 – в метрах. Определить скорость изменения ее ординаты в точке параболы
– в метрах. Определить скорость изменения ее ординаты в точке параболы 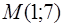 .
.
|
|
|
Вариант № 5
1. Найти производную по правилам и формулам дифференцирования
а) 
б) 
2. Функция  задана в параметрической форме
задана в параметрической форме

Найти параметрическою форму её производной 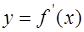 :
:

3. Показать, что функция 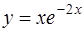 является решением уравнения
является решением уравнения 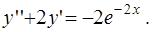
4. В каких точках касательная к кривой  параллельна оси абсцисс
параллельна оси абсцисс 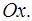
5. Тело движется прямолинейно по закону 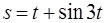 , где время
, где время  измеряется в секундах, а расстояние
измеряется в секундах, а расстояние  – в метрах. Определить скорость и ускорение тела в момент времени
– в метрах. Определить скорость и ускорение тела в момент времени 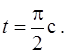
Вариант № 6
1. Найти производную по правилам и формулам дифференцирования
а) 
б) 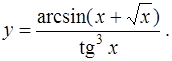
2. Функция  задана в параметрической форме
задана в параметрической форме

Найти параметрическою форму её производной 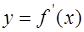 :
:
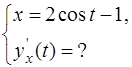
3. Показать, что функция 
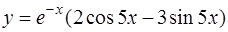 удовлетворяет уравнению
удовлетворяет уравнению 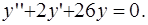
4. Найти уравнение касательной к кривой 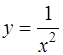 , где
, где 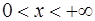 , которая параллельна прямой
, которая параллельна прямой  . Построить кривую и касательную в декартовой системе координат.
. Построить кривую и касательную в декартовой системе координат.
5. По гиперболе  движется точка так, что ее абсцисса изменяется в зависимости от времени
движется точка так, что ее абсцисса изменяется в зависимости от времени  по закону
по закону  , где
, где  измеряется в секундах, а
измеряется в секундах, а 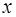 – в метрах. Определить скорость изменения ее ординаты в точке гиперболы
– в метрах. Определить скорость изменения ее ординаты в точке гиперболы 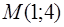 .
.
Вариант № 7
1. Найти производную по правилам и формулам дифференцирования
а) 
б) 
2. Функция  задана в параметрической форме
задана в параметрической форме

Найти параметрическою форму её производной 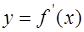 :
:
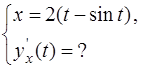
3. Показать, что функция 
 удовлетворяет уравнению
удовлетворяет уравнению 
4. Найти уравнение касательной к кривой  в точке, абсцисса которой
в точке, абсцисса которой  . Построить касательную в декартовой системе координат.
. Построить касательную в декартовой системе координат.
5. Радиус шара возрастает равномерно со скоростью 5 м/с. С какой скоростью растут площадь поверхности шара и объем шара в момент, когда радиус его становится равным 50 м?
Вариант № 8
1. Найти производную по правилам и формулам дифференцирования
а) 
б) 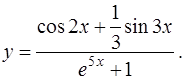
2. Функция  задана в параметрической форме
задана в параметрической форме

Найти параметрическою форму её производной 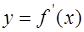 :
:

3. Показать, что функция 
 удовлетворяет уравнению
удовлетворяет уравнению 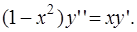
4. В какой точке касательная к параболе 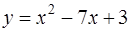 параллельна прямой
параллельна прямой  ? Найти ее уравнение. Построить параболу и касательную в декартовой системе координат.
? Найти ее уравнение. Построить параболу и касательную в декартовой системе координат.
|
|
|
5. Одна сторона прямоугольника имеет постоянную величину  м, а другая сторона
м, а другая сторона 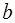 изменяется, возрастая с постоянной скоростью 4 м/с. С какой скоростью растут диагональ прямоугольника и его площадь в момент, когда
изменяется, возрастая с постоянной скоростью 4 м/с. С какой скоростью растут диагональ прямоугольника и его площадь в момент, когда  м?
м?
Вариант № 9
1. Найти производную по правилам и формулам дифференцирования
а) 
б) 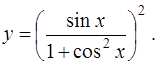
2. Функция  задана в параметрической форме
задана в параметрической форме
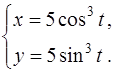
Найти параметрическою форму её производной 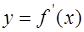 :
:
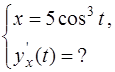
3. Показать, что функция 
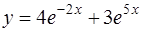 удовлетворяет уравнению
удовлетворяет уравнению 
4. Написать уравнение касательной к параболе 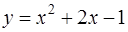 в точке ее пересечения с кривой
в точке ее пересечения с кривой  . Построить параболу
. Построить параболу 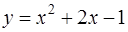 и касательную в декартовой системе координат.
и касательную в декартовой системе координат.
5. По оси  движутся две точки, имеющие законы движения
движутся две точки, имеющие законы движения 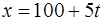 и
и 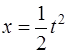 , где
, где 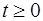 . С какой скоростью удаляются эти точки друг от друга в момент встречи (координата
. С какой скоростью удаляются эти точки друг от друга в момент встречи (координата 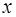 измеряется в метрах, а время
измеряется в метрах, а время  – в секундах)?
– в секундах)?
Вариант № 10
1. Найти производную по правилам и формулам дифференцирования
а) 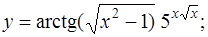
б) 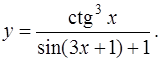
2. Функция  задана в параметрической форме
задана в параметрической форме

Найти параметрическою форму её производной 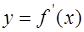 :
:
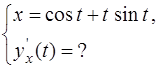
3. Показать, что функция 
 удовлетворяет уравнению
удовлетворяет уравнению 
4. Найти уравнения касательных к кривой 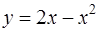 в точках пересечения её с осями координат. Построить кривую и касательные в декартовой системе координат.
в точках пересечения её с осями координат. Построить кривую и касательные в декартовой системе координат.
5. Тело движется прямолинейно по закону  , где время
, где время  измеряется в секундах, а расстояние
измеряется в секундах, а расстояние  – в метрах. Определить скорость и ускорение тела в момент времени
– в метрах. Определить скорость и ускорение тела в момент времени 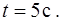
|
|
|


