 |
Крамеровские системы уравнений. Теорема Кронекера–Капелли
|
|
|
|
Система линейных алгебраических уравнений
Рассмотрим систему линейных алгебраических уравнений
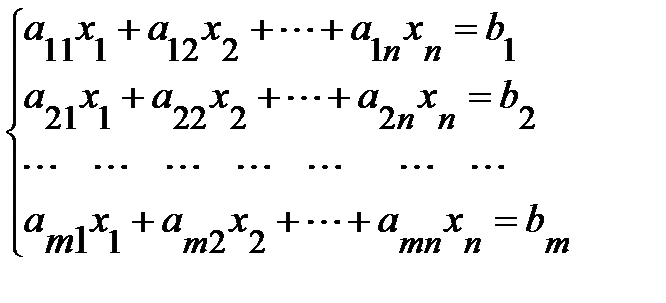, (1)
где а i j – числовые коэффициенты системы; b i - произвольные числовые константы, называемые свободными членами системы; х 1, х 2 ,…,х n – неизвестные величины, подлежащие определению.
Вводя матрицы А = 
; х = 
; b =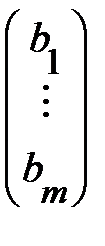 
,
систему (1) можно записать в матричном виде
Ах = b. (2)
Матрица А называется основной матрицей системы (1), а матрица
В =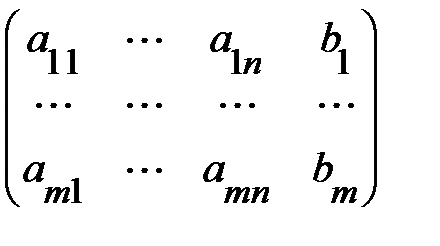 
называется расширенной матрицей системы (1).
Система (1), в которой число неизвестных n совпадает с числом m уравнений, называется крамеровской системой линейных уравнений:
m = n
Ax = b . (3)
В этом случае матрица А является квадратной матрицей n –го порядка.
Если определитель матрицы А в системе (3) отличен от нуля, то умножая матричное уравнение слева на обратную матрицу А-1, получим его решение
А - 1 Ах = А - 1 b Þ Ex = x = А - 1 b. (4)
Пример 16. Решить систему матричным методом
ì х1 + 2х2 – х3 = 8
í 2х1 – х2 + х3 = -3
î 3х1 + х2 – 2х3 = 11.
|
|
|
Решение. Имеем матрицы
А =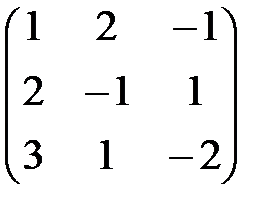 
; х = 
; b = 
.
Для применения формулы (4) необходимо вычислить обратную матрицу А - 1 (результат получен в примере 13). Окончательно получим
x = А - 1 b =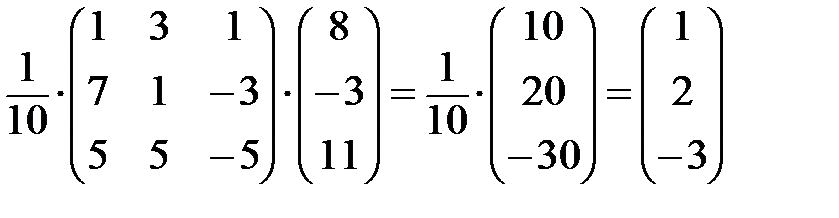 
, т.е.
х 1 = 1; х 2 = 2; х 3 = -3.
Если число неизвестных величин в системе (3) невелико, то для получения решения можно воспользоваться формулами Крамера
Х i = 
(5)
" i = 1, 2,…, n.
Пример 17. Решить систему по формулам Крамера
.
Решение. Найдем определители:
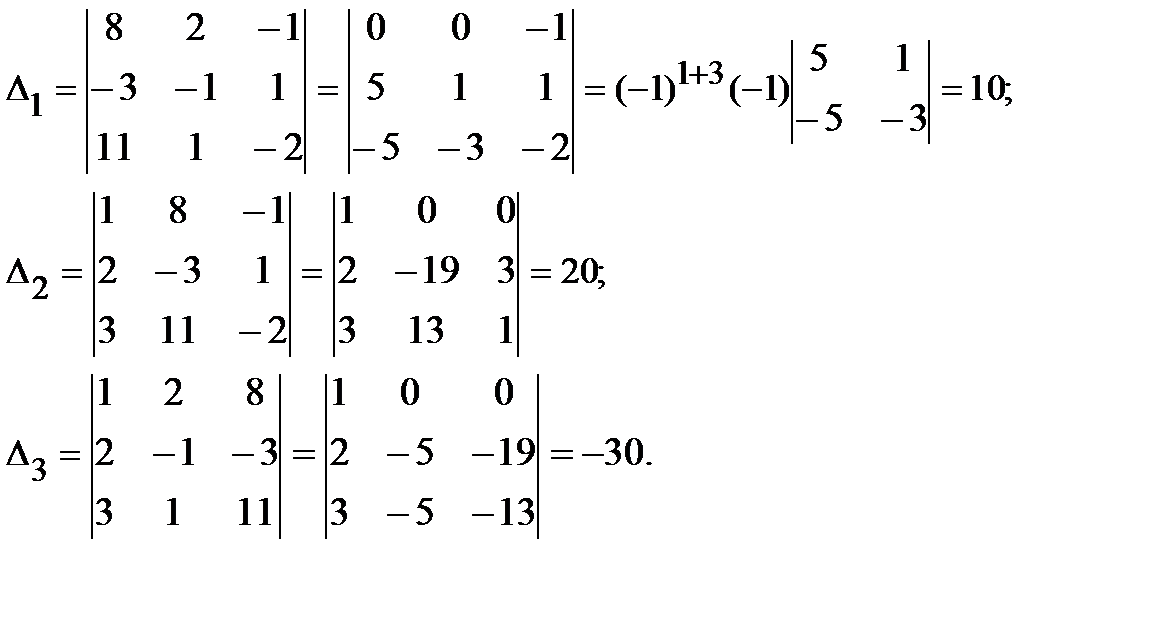
Определитель матрицы A вычислен нами ранее и равен D = det A = 10.
Применяя формулы Крамера (5), найдем решения системы:
х1= 
; х 2 = 
= 2; х3 = 
= -3.
Перейдем к решению систем линейных уравнений, заданных в общем виде (1), когда число n неизвестных величин х i i = 1,2, …, n необязательно совпадает с числом m уравнений системы.
Система линейных уравнений (1) называется однородной, если все её правые части равны нулю: b 1 = b 2 = …= b m = 0. В противном случае система (1) называется неоднородной.
Решением системы (1) называется набор таких чисел х 1, х 2, …, х n, которые обращают каждое уравнение системы в числовое тождество.
Если система (1) имеет хотя бы одно решение, то она называется совместной. Система, не имеющая ни одного решения, называется несовместной.
В частности, любая однородная система всегда совместна, так как одним из ее решений является нулевое (тривиальное) решение:
х 1 = х 2 = …= х n = 0.
Теорема Кронекера – Капелли
|
|
|
Система (1) линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы r (A) равен рангу расширенной матрицы r (B):
r (A) = r (B).
Если r (A) < r (B), то система (1) несовместна.
Если r (A) = r (B) = n (где n – число неизвестных), то система (1) имеет единственное решение.
Если r (A) = r (B) < n, то система (1) имеет бесчисленное множество решений.
Система, имеющая единственное решение, называется определенной; в противном случае система называется неопределенной.
Общий способ решения системы основан на последовательном преобразовании исходной системы к такой эквивалентной системе, для которой решения находятся достаточно просто. При этом с расширенной матрицей системы производятся действия, приводящие её к ступенчатому виду. Метод решения систем линейных уравнений таким способом называется методом Гаусса.
Пример 18 . Найти общее решение системы
.
Решение. Запишем расширенную матрицу и приведем ее к ступенчатому виду с помощью элементарных преобразований:
В = 
~ 
~ 
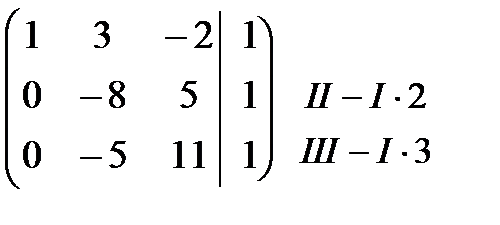= В 1.
Получим ранги r(А) = r(В 1) = 3, причем это число совпало с числом неизвестных n = 3 в данной системе. Это означает, что система имеет единственное решение. Для его нахождения запишем систему, эквивалентную данной:
.
Методом подстановки найдем решение этой системы:
х 1 = 
; х 2 = 
; х 3 =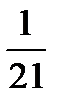 
; или Х = 
.
Пример 19. Найти общее решение системы уравнений
.
Решение. Приведем матрицу однородной системы к ступенчатому виду
А = 
~ 
= А1.
Ранг эквивалентной матрицы А 1 равен r (А 1) = 3, при этом число переменных n = 4 (замечаем, что n > r (А 1)). В этом случае какие-либо три переменные, например, х 1 , х 2 и х 3, будем называть базисными, а оставшиеся переменные, в данном случае это х 4, будем называть свободными.
Запишем систему, эквивалентную данной
|
|
|
.
Перенесем переменную х 4 в правую часть и получим
.
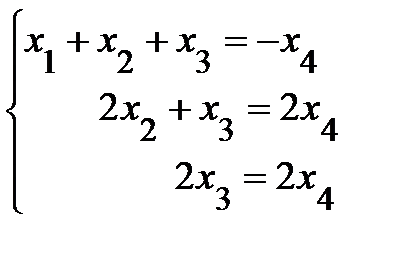Запишем основную А и расширенную В матрицы этой системы
А = 
; В =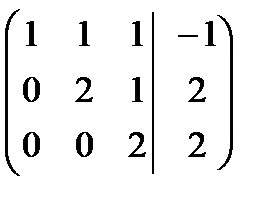 
.
Ранги этих матриц равны r (А) = r (В) = 3, причем n = 4 > r (А) = 3, поэтому система является неопределенной и имеет бесчисленное множество решений. Обозначим х 4= t и выразим базисные переменные
х 1 = 
; х 2 = 
; х 3 = t.
Общее решение исходной системы будет Х = 
.
При фиксированном значении t = t 0 (t 0 – числовое значение) из общего решения можно выделить некоторое частное решение системы
Х 0 = 
.
Вопросы для самопроверки
1. Запишите систему линейных уравнений в развернутом и матричном виде.
2. Какая система называется крамеровской системой линейных уравнений?
3. Сформулируйте правило Крамера решения систем линейных уравнений.
4. Сформулируйте правило решения систем линейных уравнений матричным методом.
5. Какие преобразования матрицы называются эквивалентными?
6. Какие системы называются совместными?
7. Сформулируйте теорему Кронекера-Капелли.
8. Какие системы называются определенными (неопределенными)?
9. В чем заключается метод Гаусса решения систем линейных уравнений?
10. Что такое матрицы линейного преобразования?
11. Запишите линейное преобразование в матричной форме.
12. Запишите в матричной форме нахождение преобразования, обратного данному линейному преобразованию.
|
|
|
