 |
Алгебраическое свойство смешанного произведения
|
|
|
|
([ a, b ], с) = (a,[ b, с ]) = (b,[ с, a ]).
Геометрическое свойство смешанного произведения
Модуль смешанного произведения |(a, b, с) | равен объёму параллелепипеда,
построенного на векторах a, b, с.
Пример 25. Даны вершины треугольника А(2,1,3), В(4,-2,4), С(5,2,1). Определить величину угла А.
Решение. Находим векторы  и
и  :
:
 = (4-2)
= (4-2)  + (-2-1)
+ (-2-1)  + (4-3)
+ (4-3) 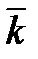 = 2
= 2  - 3
- 3  +
+ 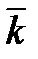 ;
;
 = (5-2)
= (5-2)  + (2-1)
+ (2-1)  + (1-3)
+ (1-3) 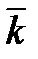 = 3
= 3  +
+  - 2
- 2 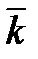 .
.
Далее: |  | =
| =  ,
,
|  | =
| =  .
.
Найдем скалярное произведение векторов  и
и  по формуле (11):
по формуле (11):
( ,
,  ) = 2× 3 + (-3)× 1 + 1× (-2) = 6 – 3 – 2 = 1.
) = 2× 3 + (-3)× 1 + 1× (-2) = 6 – 3 – 2 = 1.
Окончательно, из формулы (12) получим
сos a =  и по таблице (или с помощью калькулятора) найдем a» 850 54¢.
и по таблице (или с помощью калькулятора) найдем a» 850 54¢.
Пример 26. Вычислить площадь треугольника АВС из примера 24.
Решение. Найдем векторное произведение векторов  и
и  :
:
с =  = [
= [  ,
,  ] =
] =  .
.
По определению векторного произведения |  | численно равен площади параллелограмма, построенного на векторах сомножителей, а площадь ΔАВС равна
| численно равен площади параллелограмма, построенного на векторах сомножителей, а площадь ΔАВС равна
половине площади этого параллелограмма, т.е.
SΔABC =  кв. ед.
кв. ед.
Пример 27. Основанием пирамиды SABC служит Δ АВС из примера 24.
Вершина S (3,3,6). Найти объем пирамиды.
Решение. Для решения этой задачи учтем, что объем параллелепипеда, построенного на векторах  ,
,  и
и  как на ребрах, равен абсолютной величине смешанного произведения этих векторов, а объем пирамиды составляет 1/6 часть объема указанного параллелепипеда.
как на ребрах, равен абсолютной величине смешанного произведения этих векторов, а объем пирамиды составляет 1/6 часть объема указанного параллелепипеда.
Находим
( ,
,  ,
,  ) =
) = 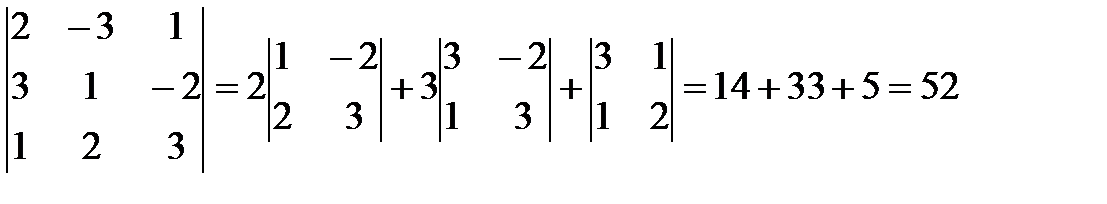 .
.
Тогда объем пирамиды V = 52/6 = 26/3 куб. ед.
Вопросы для самопроверки
|
|
|
1. Могут ли два вектора иметь равные длины, но быть неравными?
2. Могут ли два коллинеарных вектора иметь равные длины, но быть неравными?
3. Чем отличаются составляющие вектора по осям координат от его проекции на оси координат?
4. Что такое скалярное произведение двух векторов и по какой формуле оно вычисляется?
5. Что такое векторное произведение двух векторов и по какой формуле оно находится?
6. Что такое смешанное произведение трех векторов и по какой формуле оно вычисляется?
7. Как расположены ненулевые векторы a, b и с относительно друг друга, если:
а) (a, b) = 0; б) (a, b) = | a | | b |; в) [ a, b ] = 0; г) [ a, b ] = | a | | b |; д) (a, b, с) = 0; е) (a, b, с) = | a || b || с |?
8. Что называется линейной комбинацией векторов?
9. Какие векторы называются линейно независимыми?
10. Дайте определение базиса векторного пространства.
11. Что такое координаты вектора в данном базисе?
12. Что называется размерностью линейного векторного пространства?
13. Какое пространство называется евклидовым?
14. Какой базис называется ортонормированным?
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Аналитическая геометрия на плоскости
Линии и их уравнения. Уравнение прямой на плоскости
Важным понятием в аналитической геометрии является понятие уравнения линии.
Уравнением данной линии в выбранной системе координат называется такое уравнение F (x, y) = 0 с двумя переменными, которому удовлетворяют координаты х и у каждой точки, лежащей на этой линии, и не удовлетворяют координаты никакой точки, не лежащей на ней.
На этом утверждении основаны методы аналитической геометрии, суть которых состоит в том, что рассматриваемые линии исследуются при помощи анализа их уравнений. В аналитической геометрии всякую линию рассматривают как геометрическое место точек, обладающих каким-то свойством, общим для всех её точек.
|
|
|
Алгебраические уравнения линии в декартовых прямоугольных координатах в общем виде, например, имеют вид:
А х + В у + С = 0; (15)
А х 2 + В ху + С у 2 + D x + E y + F = 0, (16)
где А, В, С, D, E, F – некоторые фиксированные числа, называемые коэффициентами данных уравнений.
Уравнение (15) – уравнение первой степени и является общим уравнением прямой (или линии 1-го порядка). Здесь коэффициенты А и В одновременно не могут равняться нулю.
Уравнение (16) – уравнение второй степени и является уравнением линии второго порядка. Здесь коэффициеты А, В, и С, также одновременно не могут равняться нулю.
Порядок алгебраического уравнения определяет порядок кривой.
|
|
|


