 |
Векторы и действия над ними
|
|
|
|
Следует различать два типа объектов, встречающихся в естествознании: скалярные и векторные величины.
Скалярные величины – это величины, которые характеризуются числовым значением. Например, скалярными величинами являются масса тела, давление, коэффициент трения и т.д.
Векторные величины – это величины, которые кроме числового значения характеризуются еще направлением. Примерами таких величин являются: скорость тела, сила, действующая на тело, импульс тела и т.д.
Вектором называется направленный отрезок 
с начальной точкой А и конечной точкой В, который можно перемещать параллельно самому себе.
Длиной 
вектора = а называется число (неотрицательное), равное длине отрезка АВ, соединяющего точки А и В.
Нулевой вектор – вектор, начальная и конечная точки которого совпадают: = 
= О. Его длина равна нулю (| О | = 0), а направление для него не имеет смысла.
Единичный вектор е - вектор, длина которого равна 1 (| е | = 1). 
Коллинеарные векторы – векторы, лежащие на одной прямой или на параллельных прямых. Векторы а, b и c, изображенные на рис. 1, коллинеарны.
Рис. 1
Компланарные векторы – векторы, которые лежат в одной плоскости или в параллельных плоскостях.
Равные векторы – векторы, которые коллинеарны, имеют одинаковую длину и одинаковое направление.
Суммой а + b векторов а и b называется вектор, идущий из начала вектора а в конец вектора b, если начало вектора b совпадает с концом вектора а (т.е. вектор b приложен к вектору а) – это правило треугольника (рис. 2).
Рис. 2 Рис. 3
|
|
|
Если векторы а и b имеют общее начало и на них как на сторонах построен параллелограмм, то суммой а + b будет диагональ параллелограмма.
Правило вычитания векторов показано на рис. 3.
Произведением l а (или а l) вектора а на действительное число l называется вектор b, коллинеарный вектору а, длина которого |l а ½= |l|×| а |, а направление совпадает с вектором а, если l > 0, или противоположно а, если l < 0.
Проекцией точки А на прямую l называется точка А*, в которой пересекается прямая l с плоскостью, перпендикулярной к l, проходящей через точку А (рис. 4).
Рис. 4
Проекцией вектора а = (рис. 4) на направленную прямую l называется вектор 
, где А*и В* соответственно проекции точек А, В на прямую l.
Проекция вектора а = на направленную прямую l будем обозначать символом 
(пр l а).
Числовой проекцией |пр l а | вектора а на направленную прямую l называется произведение длины вектора а на косинус угла a между вектором а и прямой l
|пр l а | = | а |×cos (а, l) = | а |×cos a (0 £ a £p).
2. Линейное пространство. Линейная зависимость. Базис
Линейным пространством L называется множество элементов, для которых определены операции сложения двух векторов и умножения вектора на число, обладающие следующими свойствами
1. Для любых векторов а и b из линейного пространства
а + b = b + а (коммутативность сложения).
В символьной записи это свойство будет иметь вид
" a, b Î L Þ а + b = b + а.
2. " a, b,с Î L Þ(а + b) + с = а + (b + c) (ассоциативность).
3. $ О Î L: " a Î L Þ а + О = а (существование нулевого вектора).
4. " a Î L $ (- а) Î L (противоположный вектор): а + (-а) = О.
|
|
|
5. " l Î R, " a, b Î L Þ l (а + b) = l а + l b.
6. " l 1, l 2 Î R, " a Î L Þ (l 1 + l 2) а = l 1 а + l 2 а.
7. " l 1, l 2 Î R, " a Î L Þ (l 1×l 2) а = l 1(l 2 а).
8. " a Î L Þ 1× а = а.
Линейными пространствами, в частности, являются: множество действительных чисел; множество векторов на плоскости или в пространстве; множество всех функций, определенных на каком-нибудь отрезке и т.д.
Определение 21. Линейной комбинацией векторов а 1, а 2, …, а n называется
сумма с1 а1 + с2 а 2 + …+ сn а n, где коэффициенты
с1, с2, …, сn– действительные числа.
Определение 22. Совокупность векторов а 1, а 2, …, а n линейного
пространства называется линейной зависимой, если их
линейная комбинация равна нулю
с1 а1 + с2 а 2 + …+ сn а n = 0
и при этом хотя бы один из коэффициентов с1, с2, …, сn
отличен от нуля.
Определение 23. Совокупность векторов а 1, а 2, …, а n называется
линейно независимой, если равенство
с1 а1 + с2 а 2 + …+ сn а n= 0
выполняется лишь в случае, когда все коэффициенты
с1, с2, …, сn равны нулю.
Утверждение 1. Необходимым и достаточным условием линейной зависимости двух векторов на плоскости является их коллинеарность.
Утверждение 2. Необходимым и достаточным условием линейной зависимости трех векторов в пространстве является их компланарность.
Определение 24. Базисом в линейном пространстве L называется
упорядоченная система А (А = { а 1, а 2, …, а n })
максимально возможного числа векторов { а 1, а 2, …, а n},
удовлетворяющая условиям:
1) совокупность векторов а 1, а 2, …, а n линейно независима;
2) любой вектор a Î L в системе векторов А единственным
|
|
|
образом представляется в виде их линейной комбинации
а = х 1 а1 + х 2 а 2 + …+ х n а n.
Числа (х 1, х 2, …, х n) называются координатами вектора а в базисе
{ а 1, а 2, …, а n }.
Размерность линейного пространства L определяется максимальным числом n линейно независимых векторов и обозначается dim L (dim L = n). Если это число конечно, то такое пространство L называется конечномерным.
Любая пара неколлинеарных векторов а 1, а 2 на плоскости является базисом множества всех векторов, лежащих на плоскости.
Любая тройка некомпланарных векторов а 1, а 2, а 3 в трехмерном пространстве является базисом множества всех векторов, лежащих в этом пространстве.
В случае декартовой прямоугольной
системы координат в трехмерном
пространстве в качестве базисных выбирают
единичные векторы
i = (1,0,0), j = (0,1,0), k = (0,0,1),
которые:
а) линейно независимы;
б) имеют длину, равную единице, т.е. | i | = | j | = | k | = 1;
c) по направлению совпадают с направлением осей
Рис. 5 координат OX, OY, OZ.
Векторы i, j, k называются ортами и образуют базис.
Любой произвольный вектор а в этом трехмерном базисе может быть представлен в виде линейной комбинации а = х i + у j + z k или а = (х, у, z), где х, у, z - координаты ветора а в базисе { i, j, k }.
3. Собственные значения и собственные векторы матрицы.
Характеристическое уравнение
Во многих областях науки и техники, например, электро- и радиотехнике, механике, экономике, в теории кодирования и обработки сигналов широко используется понятие «собственное значение» и «собственный вектор».
Определение 25. Число l называется собственным значением, а ненулевой вектор х называется собственным вектором матрицы А, задающей линейное преобразование, если они связаны между собой соотношением
|
|
|
А х = l х Û (А -l Е) х = О. (8)
Это матричное уравнение задает систему однородных линейных уравнений:
, (9)
которая имеет ненулевое решение в том случае, когда ее определитель | А -l Е | равен нулю.
Определение 26. Характеристическим уравнением квадратной матрицы А называется уравнение
| А -l Е | = 0.
Пример 24. Найти собственные значения и собственные векторы линейного
преобразования с матрицей А = 
.
Решение. Составим характеристическое уравнение | А -l Е | = 0 Þ
(7 -l)[(5 -l)(6 -l) - 4] + 2 × (-2)(5 -l) =
= -l3 + 18l2- 99l + 162 = 0 Þ (l-3)(l- 15l + 54) = (l- 3)(l- 6)(l- 9) = 0.
Таким образом нашли собственные значения линейного преобразования с матрицей А, равные: l1 = 3, l2 = 6, l3 = 9.
Найдем собственный вектор, соответствующий собственному значению
l1=3. Подставим l = 3 в систему (9) и получим 
.
С помощью элементарных преобразований получим систему, эквивалентную
данной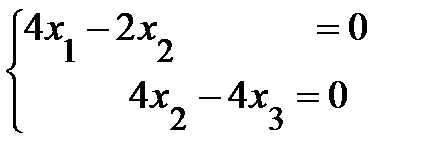 
, ранг которой r = 2. Так как число неизвестных в
системе n = 3 > r = 2, то в качестве базисных выберем переменные х1 и х2, а свободной переменной будет х3. Полагая х3= 2 t, где t – произвольное число, из последней системы найдем: х2 = 2 t, х1 = t.
Таким образом собственному значению l1 = 3 соответствует собственный
вектор Х 1 = 
. Аналогично, собственным значениям l2 = 6 и l3 = 9 соответствуют собственные векторы Х 2 = 
и Х 3 = 
.
|
|
|
