 |
Уравнение прямой на плоскости
|
|
|
|
Прямая линия на плоскости может быть задана различными способами.
1. Общее уравнение прямой на плоскости в прямоугольной системе ОХУ:
А х + В у + С = 0.
Прямая, определяемая этим уравнением, ортогональна к вектору n, координаты которого А и В, т.е. n = {A,B}.
Вектор n – нормальный вектор данной прямой.
2. Уравнение прямой, проходящей через заданную точку М(х 0, у 0):
А(х - х 0) + В(у - у 0) + С = 0.
3. Уравнение прямой в отрезках:
,
где а = 
и b = 
.
4. Каноническое уравнение прямой:
,
где m и n – координаты направляющего вектора L = { m, n } (параллельного данной прямой).
5. Уравнение прямой, проходящей через две данные точки М 1 (х1, у1) и
М2 (х2, у2):
.
6. Параметрическое уравнение прямой
,
где t – параметр, т.е. при одном и том же значении t эти уравнения определяют координаты х и у некоторой точки линии. При изменении параметра t изменяются х и у, и соответствующая точка перемещается вдоль заданной линии.
7. Уравнение прямой с угловым коэффициентом k = 
у – у 0 = k (х – х 0) или у = k х + b.
8. Нормальное уравнение прямой
xcos a + ysin a – p = 0,
где a – угол между нормальным вектором n к данной прямой и осью ОХ;
p – длина отрезка прямой, совпадающего по направлению с вектором n и соединяющего начало координат с заданной прямой.
|
|
|
При решении различных задач то или иное из этих уравнений оказывается удобным. Поэтому надо научиться приводить уравнение прямой к любому из указанных видов, когда это возможно (например, прямая, параллельная оси ординат, не может быть представлена уравнением с угловым коэффициентом), и хорошо уяснить геометрический смысл параметров А, В, m, n, a, b в указанных уравнениях.
Не следует думать, что все способы построения прямой по её простейшим уравнениям одинаково удобны. Обычно построение прямой легче всего производить, исходя из её уравнения в отрезках.
Необходимо научиться проводить прямую через данную точку в заданном направлении и прямую через две заданные точки, уметь определять угол между двумя прямыми, применять условия параллельности и перпендикулярности двух прямых. Следует обратить внимание на то, что в аналитической геометрии «провести» означает «написать уравнение».
Пример 28. Вершины треугольника находятся в точках А (-4, 16), В (-10, -1) и
С (14, -8).
Найти длину высоты, опущенной из вершины В, и величину угла А.
Решение. 1. Находим уравнение прямой АС как прямой, проходящей через две заданные точки:
.
Отсюда угловой коэффициент прямой k АС = 
.
Длина высоты ВС (| ВС | = h) равна расстоянию от точки В до прямой АС, которое можно найти по формуле расстояния между заданной точкой М (х 0, у 0) и прямой Ах +Ву + С = 0:
h = 
.
В нашем случае h = 
ед. дл.
2. Для нахождения угла А находим уравнение прямой АВ:
,
откуда 17х – 6у + 164 = 0 или у = 
.
Итак, k 1 = k AB = 
, а k 2 = k AC = - 
(было найдено ранее).
Тогда tg A = 
.
Из чертежа видно, что угол А – острый. По калькулятору или по таблицам В.М.Брадиса находим: Ð А» 56 019¢ (или в радианах Ð А» 0,98 рад.).
|
|
|
Замечание. Угол А можно найти и другим способом: как угол между нормальными векторами прямых АВ и АС по формуле
сos j = 
,
по таблице j» 56 019¢.
Вопросы для самопроверки
1. Какие виды уравнения на плоскости вы знаете?
2. Объясните смысл параметров в каждом из видов уравнения прямой.
3. Как определяется угол между прямыми на плоскости?
4. В чем заключается условие параллельности и перпендикулярности двух прямых на плоскости?
1.3 Кривые второго порядка
Кривые второго порядка – линии, определяемые в декартовых координатах алгебраическими уравнениями второй степени (16):
А х 2 + В ху + С у 2 + D x + E y + F =0.
Такими линиями являются – эллипс, гипербола, парабола, пара прямых. Они часто встречаются в различных вопросах естествознания и техники. Например, детали круглой формы и вращательное движение в технике; движение планет и искусственных спутников Земли по эллипсам; для функции у = 
графиком является гипербола; при сложении двух взаимно перпендикулярных гармонических колебаний, сдвинутых по фазе на 
,
получается уравнение эллипса 
.
Окружность является частным случаем эллипса (когда a = b), но целесообразно её самостоятельное изучение.
Следует знать канонические и параметрические уравнения окружности, эллипса, гиперболы и параболы.
При определенных соотношениях между коэффициентами А, В, С, D, E из уравнения (16) следуют канонические уравнения эллипса, гиперболы и параболы. Сведем их для удобства в таблицу 1.
Таблица 1
| Эллипс | Гипербола | Парабола | |
| Каноническое уравнение | 
| 
| 
|
| Малая полуось | 
| 
| __ |
| Эксцентриситет | 
| 
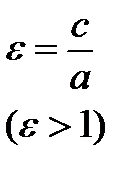
| e = 1 |
| Асимптоты | ¾- | 
| ¾ |
| Фокальные радиусы | z 1 = a + e x z 2 = a -e x | правая ветвь z1 = e x + a z2 = e x - a левая ветвь z 1 = -e x - a z 2 = -e x + a |
|
| Директрисы | 
| 
| 
|
|
|
|
Вопросы для самопроверки
1. Что такое эллипс и каково его каноническое уравнение?
2. Что такое гипербола и каково ее каноническое уравнение?
3. Что такое парабола и каково ее каноническое уравнение?
4. Что такое эксцентриситет и каким он может быть у эллипса, у
гиперболы, у параболы?
5. Какие из кривых второго порядка имеют асимптоты и каковы их
уравнения?
6. Какая линия называется алгебраической и как определяется ее порядок?
2. Аналитическая геометрия в пространстве
|
|
|
