 |
Различные виды уравнения плоскости
|
|
|
|
1. Можно доказать утверждение, что если в пространстве задана прямоугольная система координат ОХУZ, то всякое уравнение первой степени с тремя неизвестными х,у,z необходимо и достаточно определяет относительно этой системы некоторую плоскость Р. Уравнение это называется общим уравнением плоскости и имеет следующий вид:
А х + В у + С z + D= 0 (17)
(сравните с общим уравнением (15) прямой на плоскости, которое следует из этого при z = 0) и определяет плоскость Р, перпендикулярную вектору  (А,В,С).
(А,В,С).
Вектор  - нормальный вектор плоскости Р.
- нормальный вектор плоскости Р.
Уравнению (17) эквивалентны следующие уравнения.
2. Уравнение плоскости, проходящей через заданную точку М(х0, у0, z0):
А(х - х 0) + В(у - у 0) + С(z - z 0) = 0.
3. Уравнение плоскости в отрезках
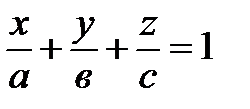 ,
,
где  ;
;  ;
;  .
.
4. Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой, записывается в виде определителя
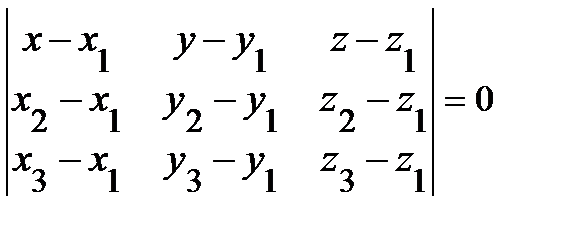 ,
,
где (х 1, y 1, z 1), (х 2, y 2, z 2), (х 3, y 3, z 3) - координаты заданных точек.
Угол между двумя плоскостями определяется как угол между их нормальными векторами n 1 и n 2. Отсюда условие параллельности плоскостей
Р 1 и Р 2:

и условие перпендикулярности двух плоскостей:
А 1 А 2 + В 1 В 2 + С 1 С 2 = 0.
Пример 29. Через точку К (1, -3, 2) провести плоскость, параллельную векторам
а = (1, 2, -3) и b = (2,-1,-1).
Решение. Пусть М (х, у, z) – произвольная точка искомой плоскости. Вектор
|
|
|
КМ = (х - 1, у + 3, z - 2) лежит в этой плоскости, а векторы а и b ей параллельны. Следовательно, векторы КМ, а и b – компланарны. Тогда их смешанное произведение равно нулю:
 .
.
Отсюда -(х –1) - (у + 3) – 5(z – 2) = 0 или х+ 7 у + 5 z + 10 = 0. Это и есть искомое уравнение плоскости.
Различные виды уравнения прямой в пространстве
Прямую линию в пространстве можно задавать в виде:
1) линии пересечения двух не совпадающих и не параллельных плоскостей Р 1 и Р 2:
 ;
;
2) уравнения прямой, проходящей через данную точку М (х 0, у 0, z 0) в направлении, задаваемом вектором L = (m, n, p):
 ,
,
которое называется каноническим уравнением прямой в пространстве;
3) уравнения прямой, проходящей через две заданные точки М (х 1, у 1, z 1)
и M (x 2, y 2, z 2):
 ;
;
4) параметрических уравнений:
 .
.
Пример 30. Привести к каноническому и параметрическому видам уравнение прямой
 .
.
Решение. Прямая задана как линия пересечения двух плоскостей. Нормальные векторы этих плоскостей n 1 = (3,1,-2) и n 2 = (4,-7,-1) перпендикулярны к искомой прямой, поэтому их векторное произведение [ n 1, n 2] = L параллельно ей и вектор [ n 1, n 2] (или любой ему коллинеарный) можно принять за направляющий вектор L искомой прямой.
Находим
[ n 1, n 2] =  .
.
Примем за L = 3 i + j + 5 k. Остается найти какую-либо точку на заданной прямой. Положим для этого, например, z = 0. Получим
 .
.
|
|
|
Решив эту систему, находим х = 1, у = - 2. Таким образом, точка К (1, -2, 0) принадлежит заданной прямой, а её каноническое уравнение имеет вид
 .
.
Параметрические уравнения следуют из канонических, если за параметр t принять каждое из отношений:
 ;
;  ;
;  .
.
Откуда  .
.
Пример 31. Через точку К (1, 3, -1) провести прямую, перпендикулярную
плоскости 3 х – у + 2 z – 10 = 0.
Решение. Вектор нормали к данной плоскости n = (3, -1, 2). Искомая прямая проходит через точку К и должна быть параллельна вектору n. Поэтому её уравнение можно записать в виде
 .
.
Вопросы для самопроверки
1. Объясните смысл параметров в уравнениях
 ;
;  .
.
2. Напишите уравнения:
а) плоскости ХОZ;
б) осей ОУ, ОХ, ОZ.
3. Каково взаимное расположение прямой

и плоскости 3 х + 2 у – 5 = 0?
2.3 Поверхности 2-го порядка
Студент должен уметь распознавать указанные в таблице две поверхности 2-го порядка по их каноническим уравнениям, используя при этом метод сечений.
Таблица 2
| Каноническое уравнение | Название | Схематический чертеж |

| Трехосный эллипсоид | 
|

| Однополостный гиперболоид | 
|

| Двуполостный гиперболоид | 
|

| Эллиптический параболоид | 
|

| Гиперболический параболоид | 
|

| Конус 2-го порядка | 
|
Следует, также, обратить внимание на цилиндры 2-го порядка
 ;
;  ; у 2= 2 рх
; у 2= 2 рх
и на поверхности вращения 2-го порядка. Например, если в уравнении однополостного гиперболоида
|
|
|

Положить а = b, то в сечении поверхности плоскостью z = h будут получаться окружности
 ,
,
следовательно, в этом случае поверхность является однополостным гиперболоидом вращения (он получается вращением гиперболы
 вокруг оси ОZ).
вокруг оси ОZ).
Пример 32. Составить уравнение поверхности, образованной вращением линии x 2 - pz 2 = 4 вокруг оси OZ. Подобрать значение параметра р так, чтобы точка А (1,2,-1) лежала на этой поверхности. Указать название полученной поверхности и сделать её эскиз.
Решение. Уравнением вращения линии F(x,z) = 0 вокруг оси OZ является уравнение
 ,
,
так как при вращении вокруг оси OZ в уравнении без изменения остается координата z, а х заменяется на  (аналогичный факт имеет место и по отношению к поверхностям, получаемым вращением плоских линий вокруг других координатных осей).
(аналогичный факт имеет место и по отношению к поверхностям, получаемым вращением плоских линий вокруг других координатных осей).
Таким образом, в рассматриваемом примере получим уравнение
 или x 2 + y 2 – pz 2 = 4.
или x 2 + y 2 – pz 2 = 4.
Найдем параметр р, учитывая требования задачи. Координаты точки А должны удовлетворять найденному уравнению поверхности. Подставляя координаты точки в уравнение, получим 1+ 4 - р = 4 Þ р = 1. Тогда искомое уравнение примет вид
x 2 + y 2 – z 2 = 4 или в канонической форме  .
.
Это уравнение описывает однополостный гиперболоид вращения.
Пример 33. Построить поверхность, определяемую уравнением:
9 x 2 + 4 y 2+ 36 z 2 -18 x - 16 y +216 z + 313 = 0.
Для выполнения задания необходимо:
а) привести данное уравнение поверхности к каноническому виду;
б) определить вид поверхности и ее расположение относительно системы координат;
с) записать название поверхности и сделать чертеж.
Решение. Группируем члены уравнения, содержащие одинаковые переменные:
(9 x 2 - 18 x) + (4 y 2 - 16 y) + (36 z 2 + 216 z) + 313=0 Þ
|
|
|
9(x 2 - 2 x) + 4(y 2 - 4 y) + 36(z 2 + 6 z) + 313=0.
Выделяем полный квадрат в каждой скобке:
9((x 2 - 2 x +1) - 1) + 4((y 2- 4 y + 4) - 4)+36((z 2+ 6 z + 9) - 9) + 313 = 0.
Получим 9((x -1) 2-1) + 4((y -2) 2- 4) + 36((z +3) 2-9) + 313 = 0 Þ
9(x -1) 2-9 + 4(y -1) 2-16 + 36(z +3) 2-324 + 313=0 Þ
9(x -1) 2 + 4(y -2) 2 + 36(z + 3) 2 = 36.
Разделим обе части уравнения на свободный член и получим каноническое уравнение эллипсоида с центром в точке О1(1,2,-3)
 .
. 
Для построения этого эллипсоида сделаем в уравнении замену переменных
x -1= x 1, y -2 = y 1, z +3 = z 1.
В новых переменных уравнение эллипсоида примет вид:
 .
.
Сделаем чертеж. Для этого через центр эллипсоида O1(1,2,-3) проведем оси
O1X1 , O1Y1, O1Z1, и в этой системе координат построим эллипсоид
 , где a = 2, b = 3, c = 1 (рис. 7).
, где a = 2, b = 3, c = 1 (рис. 7).

Рис. 7
Вопросы для самопроверки
1. Какие поверхности заданы уравнениями:
4 x 2+9 y 2+ z 2 = 36;
4 x 2+9 y 2- z 2 = 36;
4 x 2+9 y 2- z 2= -36;
3 x 2+4 y 2 = z 2;
3 x 2- 4 y 2= z 2;
x 2+ y 2 = z;
x 2+ z 2= 1;
x 2– z 2= 0;
y 2= 4 x.
2. Составить уравнение поверхности, образованной вращением прямой
у = k х вокруг оси ОХ.
3. Какую поверхность в пространстве описывает алгебрарическое уравнение 2-го порядка, содержащее лишь две переменные?
Контрольная работа № 1
Вариант 0
1. Решить систему линейных уравнений матричным методом и по формулам Крамера.
| Варианты | Варианты | ||
| 10 | -5x +4y -3z = 6 -6x - 2y +5z = 9 4x - y - 3z = -8 | 60 | -3x + 4y +5z = -4 -5x +5y +5z = -5 2y - z = 3 |
| 20 | -2y +3z = -8 3x +y +3z = 1 -x +y +z = -3 | 70 | 3x - 4y - 4z = - 6 5x + 3y + z = - 8 4x + 2y - 3z = -3 |
| 30 | -y - 5z = 2 -5x +y +2z = - 4 -5x +5y +4z = 6 | 80 | 3x +4y -z = -8 y - 2z = -8 -3x -y +3z = 8 |
| 40 | -4x -6y -z = -1 -x -2y -5z = 5 -x +2z = -4 | 90 | -x -3z = 5 3x -2y -z = 3 -x +6y -2z = 9 |
| 50 | x +4y +z = 7 -3x +2y +z = -1 5x -2y -2z = 5 | 00 | -x -3y = 5 -3x +y +z = -2 -2x +y +3z = 5 |
2. Даны координаты вершин треугольника АВС. Требуется:
1) вычислить длину стороны ВС;
2) составить уравнение стороны ВС;
3) вычислить длину высоты, проведенной из вершины А;
|
|
|
4) составить уравнение этой высоты.
| Варианты | 10 | 20 | 30 | 40 | 50 |
| А(x1;y1;) В(x2;y2;) С(x3;y3;) | (-5, -3) (-7, -9) (-13, -17) | (-19, -10) (6, -15) (14, -9) | (10, 15) (-14, -13) (-17, -9) | (16, 8) (-11, 4) (-15, 1) | (19, -1) (-4, -7) (-16, -16) |
| Варианты | 60 | 70 | 80 | 90 | 00 |
| А(x1;y1;) В(x2;y2;) С(x3;y3;) | (4, -8) (-9, -4) (-13, -7) | (-19, -7) (-5, -15) (4, -3) | (-6, 6) (-4, 0) (5, -12) | (19, -4) (13, 8) (17, 5) | (-10, 4) (-18, 5) (-10, -1) |
3. Даны координаты вершин пирамиды А1А2А3А4. Средствами векторной алгебры найти:
1) угол между ребрами А1А2 и А1А4;
2) площадь грани А1А2А3;
3) объем пирамиды А1А2А3А4;
4) уравнение плоскости основания пирамиды А2А3А4;
5) уравнение высоты пирамиды, проведенной из вершины А1.
| Варианты | 10 | 20 | 30 | 40 | 50 |
| (7, 2, -9) (3,-5,-5) (7,-8,-9) (1, 5, -7) | (6,-4,-5) (6,-7,-9) (-2, 2,-5) (6, 3, -5) | (3, 3, 6) (1, 3, 6) (1,-3, 3) (10,-1,10) | (-6, -7, 1) (-3, -5, 7) (1, -1, 7) (-6, -7, 6) | (3, 3, -5) (4, 5, -7) (9, 6, -3) (-4, -3, 1) | |
| Варианты | 60 | 70 | 80 | 90 | 00 |
| (-7, 8, 2) (-1, 5, 4) (-5, 10, 1) (-7, 8, 1) | (2, 4, 4) (-4,-3, -2) (5, 2, -2) (-2, -4, 5) | (-2, -1,-7) (2,-1,-7) (-2,-1, -6) (-4,-3,-8) | (1, 5, -1) (10, 3, 5) (1, 5, -9) (7, 5, -1) | (-1, 5, 5) (-3, 6, 3) (-1, 5, 2) (6, 9, 1) |
4. 1) Составить уравнение поверхности, образованной вращением линии вокруг оси ОZ.
2) Подобрать значение параметра p так, чтобы точка А(x0;y0;z0) лежала на поверхности.
3) Сделать схематический чертёж.
| Варианты | Данные | задачи |
| Уравнение линии в плоскости х = 0 | А(x0;y0;z0) | |
| 10 | рy2 = z | (1, 0,-1) |
| 20 | рy2 + 2z2 = 2 | (1,-1, 0) |
| 30 | y2 = рz2 +р | (1, 3, 2) |
| 40 | y2 + рz2 = 6р | (1, 2, -1) |
| 50 | рy2 + z2 = 6 | (1,-1, 2) |
| 60 | y2 = z2 + р | (4, 3, 5) |
| 70 | рy2 = рz + 4 | (1,-2, 1) |
| 80 | рy2 + z2 = 4р | (2, 1,-2) |
| 90 | рy2 + z2 = 4 | (0, 1, 1) |
| 00 | y2 + z2 = 6р | (2, -1, 1) |
Вариант 1
1. Решить систему линейных уравнений матричным методом и по формулам Крамера
| Варианты | Варианты | ||
| 01 | 3x + 4y - 2z = 1 x + 5y + z = 0 2x + 4y + 3z = 8 | 51 | 2x - 5y + z = 1 4x + 2y - 3z = 1 x - y + z = 2 |
| 11 | 3x + 2y + z = 1 2x - 3y + 2z = 9 x - 8y - 5z = -7 | 61 | 3x + 3y - 2z = 4 5x - 7y + 4z = 0 x + 2y - z = 3 |
| 21 | 2x - y - z = 0 2x + 4y - z = 15 3x - z = 5 | 71 | x + 2y - 2z = 3 5x + 4y - 3z = 4 3x + y - 4z = 7 |
| 31 | x + 2y - 3z = -3 2x - 3y + z = - 13 3x + y + 2z = 4 | 81 | 5x - y + 8z = 7 2x + 2y - 3z = 9 x + 3y + 2z = 1 |
| 41 | x - 2y + 2z = -14 2x - y + z = -4 4x + y + 2z = 7 | 91 | 2x - 3y - 4z = -1 x + y + 5z = 0 3x + 2y + 4z = 8 |
2. Даны координаты вершин треугольника АВС. Требуется:
1) вычислить длину стороны ВС;
2) составить уравнение стороны ВС;
3) вычислить длину высоты, проведенной из вершины А;
4) составить уравнение этой высоты.
| Варианты | 01 | 11 | 21 | 31 | 41 |
| А(x1;y1;) В(x2;y2;) С(x3;y3;) | (-4. 3) (-10, 6) (2, -10) | (-16, 13) (14, 3) (20, 11) | (10, 11) (-6, 14) (-2, 17) | (4, 9) (-9,-2) (-18, 10) | (8,-5) (-7,-10) (9, 2) |
| Варианты | 51 | 61 | 71 | 81 | 91 |
| А(x1;y1;) В(x2;y2;) С(x3;y3;) | (-10, 20) (-5,-5) (-15, 19) | (17,-19) (9, 15) (-15, 19) | (10,-6) (-3,-6) (7, 18) | (10,-16) (1,-18) (-11,-9) | (11,-15) (-3, 8) (1, 5) |
3. Даны координаты вершин пирамиды А1А2А3А4. Средствами векторной алгебры найти:
1) угол между ребрами А1А2 и А1А4;
2) площадь грани А1А2А3;
3) объем пирамиды А1А2А3А4;
4) уравнение плоскости основания пирамиды А2А3А4;
5) уравнение высоты пирамиды, проведенной из вершины А1.
| Варианты | 01 | 11 | 21 | 31 | 41 |
| А1(x1;y1;z1) А2(x2;y2;z2) А3(x3;y3;z3) А4(x4;y4;z4) | (3, 1,-3) (3,-6,-3) (9,-6,-9) (2,-3, 5) | (-2,-4,-7) (-6,-8,-9) (-2, 1,-7) (-2,-8,-4) | (-1, 4,-4) (-4, 4,-8) (-9, 8,-3) (-5, 5, 4) | (4,-7, 8) (8,-3, 10) (2,-3, 4) (-2, 1, 8) | (-1,-3,-1) (1,-6,-7) (7,-9,-1) (1, 3, 8) |
| Варианты | 51 | 61 | 71 | 81 | 91 |
| А1(x1;y1;z1) А2(x2;y2;z2) А3(x3;y3;z3) А4(x4;y4;z4) | (5, 3, 1) (5, 3,-4) (-1,-6,-1) (-4, 1, 7) | (-2,-10,-1) (-1,-8, 1) (-6,-3, 3) (-5,-4, 1) | (2,-5,-7) (-4,-3, 2) (-2,-1,-9) (-6, 1,-7) | (8, 3,-5) (6, 7,-1) (8, 3,-10) (2,-3,-2) | (-1, 8, 3) (1, 8, 3) (-1, 4, 6) (1,-1,-3) |
4. Построить поверхность, определяемую заданным уравнением
| Вариант | Уравнение поверхности |
| 01 | x2+2x +2y2 +4y -z2 = 0 |
| 11 | x2 –4x + 4y2 –8y + z2 = 0 |
| 21 | 0,5x2 +0,25y2 –2z +2 = 0 |
| 31 | x2–2x+y2–4y +z2–6z = 0 |
| 41 | x2–6x +y2–2y–z2 –4z = 0 |
| 51 | x2 + y2 –2х – 4y = 0 |
| 61 | x2 – 4x – y2 – 2y = 0 |
| 71 | x2 – 4x + 2z = 0 |
| 81 | x2 -3x -y2 + 4y -2z2 = 0 |
| 91 | x2 – 4x +y2 – 2y – z = 0 |
Вариант 2
1. Решить систему линейных уравнений методом Гаусса
| Варианты | Варианты | ||
| 02 | 3x + 2z + u = –5 –4x–3y +5z–2u =–1 –2x–4y+6z+u = 4 –x–3y+ 7z – u =–6 | 52 | x–3y + 4z +2u = –3 –y –5z –3u = 5 2x +2y –z +u = –2 2x +y –6z –2u = 4 |
| 12 | 2y +3z –u = 9 –2x –6y +z +2u =–2 –2x –5y –3z +u =–8 –2x –4y +4z +u = 8 | 62 | –2x +4y +4z +u =–4 5x –5y –3z +u = –3 3y +3z +u = –2 –2x +7y+7z+4u =–6 |
| 22 | –x +3y +2z+3u = –7 –4x +6y –6z –2u =8 –2x +5y –u = 3 –6x+11y–6z–3u=11 | 72 | 6x –3y –6z –3u = 6 –3x –4y +6z –u = 6 6x +4y –4z +2u = 4 3x +2z + u = 9 |
| 32 | 4x +4y –z –2u = 5 –3y +3z –u = 5 –2x –y –z –u = –7 4x +y +2z –3u = 11 | 82 | –5x+2y +4z+3u =–3 –3x –4y +6z –u = 6 4x –5y –3z –3u = 5 x –9y +2z –5u = 6 |
| 42 | 6x +y –z +u = –8 5x +4y +z –3u = 4 –x –2y +4z +2u = 5 11x +5y –2u = –4 | 92 | 4x –2y +z +2u = –7 –3x –5y –z –2u =–9 y –6z +3u = 6 –3x –2y–7z +u = –2 |
2. Даны координаты вершин треугольника АВС. Требуется:
1) вычислить длину стороны ВС;
2) составить уравнение стороны ВС;
3) вычислить длину высоты, проведенной из вершины А;
4) составить уравнение этой высоты.
| Варианты | 02 | 12 | 22 | 32 | 42 |
| А(x1;y1;) В(x2;y2;) С(x3;y3;) | (20, -7) (-19, 15) (-7,-1) | (0, 4) (7,-10) (15,-16) | (-12, 19) (3, 3) (15,-2) | (-18, 8) (12, 8) (16, 11) | (17, 18) (8, 11) (-7,-9) |
| Варианты | 52 | 62 | 72 | 82 | 92 |
| А(x1;y1;) В(x2;y2;) С(x3;y3;) | (-14, 1) (-7,-10) (-3,-7) | (14,-9) (-10,-12) (0, 12) | (-18, 20) (0, 9) (-12,-7) | (14, 3) (15, -2) (-9,-12) | (-4,-9) (15,-12) (12,-16) |
3. Даны координаты вершин пирамиды А1А2А3А4. Средствами векторной алгебры найти:
1) угол между ребрами А1А2 и А1А4;
2) площадь грани А1А2А3;
3) объем пирамиды А1А2А3А4;
4) уравнение плоскости основания пирамиды А2А3А4;
5) уравнение высоты пирамиды, проведенной из вершины А1.
| Варианты | 02 | 12 | 22 | 32 | 42 |
| А1(x1;y1;z1) А2(x2;y2;z2) А3(x3;y3;z3) А4(x4;y4;z4) | (2,-5, 2) (-4,-3,-7) (-2, 2, 6) (4, 1, 5) | (2,-3, 2) (-2,-3, 5) (8,-1, 5) (-5,-9,-4) | (4, 4,-7) (4,-2, 1) (10,1,-5) (4,-7,-7) | (-4, 5,-7) (2, 5, 1) (-4, 9,-7) (-5, 3,-9) | (-1, 8,-9) (8, 2,-7) (8, 8,-9) (-1, 7,-9) |
| Варианты | 52 | 62 | 72 | 82 | 92 |
| А1(x1;y1;z1) А2(x2;y2;z2) А3(x3;y3;z3) А4(x4;y4;z4) | (-3, 4, 2) (5, 3, 6) (3, 10, 9) (5, 3,-2) | (5, 5, 2) (3, 5, 2) (6, 1, 10) (5, 5,-7) | (-3,10,-2) (-5, 8,-1) (5, 9,-6) (3, 3, 4) | (5, 4, 1) (6, 4, 1) (5, 4, 4) (3, 7, 7) | (1,-4, 3) (2,-4, 3) (8, 2, 9) (1,-4, 7) |
4. 1) Составить уравнение поверхности, образованной вращением линии вокруг оси ОХ.
2) Подобрать значение параметра p так, чтобы точка А(x0;y0;z0) лежала на поверхности.
3) Сделать схематический чертёж.
| Варианты | Данные | задачи |
| Уравнение линии в плоскости y = 0 | А(x0;y0;z0) | |
| 02 | px –2 = z2 | (2;-2; 2) |
| 12 | x + p = z2 | (1; 3; 2) |
| 22 | px2 = z2 | (1; 0; -1) |
| 32 | px = z2 | (2; -2; 2) |
| 42 | px2 = z2 – 4 | (2; -5; 1) |
| 52 | 5x2 + pz2 = 10 | (2; 3; 3) |
| 62 | p – x2 = z2 | (2; 1; 1) |
| 72 | px2 + z2 = 4 | (0; 1; 1) |
| 82 | px2 + z2 = 0 | (1;-2; 1) |
| 92 | px + 4 = z2 | (1;-1; 2) |
Вариант 3
1. Решить систему линейных уравнений матричным методом и по формулам Крамера
| Варианты | Варианты | ||
| 03 | x +2y –2z = –1 –3x +2y +4z = –9 3x –4y –z = 7 | 53 | –3x –2y +3z = –5 –3x +2y – z = –9 5x –3y –3z = 6 |
| 13 | 2x +y +4z = 5 –3x –y +2z = 2 –x – 4z = –3 | 63 | 6x +3y = 9 5x +2y +2z = 9 –5x +4y –5z = –6 |
| 23 | –5x –3y +6z = –2 5x +3y –4z = 4 –6x –2y +3z = –5 | 73 | 3x –6y –3z = 9 4x +5y –3z = –3 –x –4y +6z = –7 |
| 33 | –x +4y +z = –8 4x –4y +3z = 1 –2x +5y –3z = –5 | 83 | 4x +3y –4z = 1 –6x –3y +3z = –6 –y –z = 0 |
| 43 | 5x +2y +4z = 8 5x +y +3z = 7 3x –2y –2z = 4 | 93 | 5x + y = 6 5x +3y +3z = –1 –x –4y –4z = 7 |
2. Даны координаты вершин треугольника АВС. Требуется:
1) вычислить длину стороны ВС;
2) составить уравнение стороны ВС;
3) вычислить длину высоты, проведенной из вершины А;
4) составить уравнение этой высоты.
| Варианты | 03 | 13 | 23 | 33 | 43 |
| А(x1;y1;) В(x2;y2;) С(x3;y3;) | (-11, 0) (4, 0) (-5, 12) | (4, -16) (-14,-17) (-19,-5) | (8, 4) (-2, 14) (2,17) | (12, 17) (9, 1) (13, 4) | (18, 17) (-5, 16) (-13, 10) |
| Варианты | 53 | 63 | 73 | 83 | 93 |
| А(x1;y1;) В(x2;y2;) С(x3;y3;) | (3, -2) (0, 20) (15, 12) | (-3,-2) (19, 18) (3,-12) | (7, 2) (2, 7) (14, 16) | (-5, 2) (1,-20) (-19,-5) | (16, 13) (20,-20) (-4,-2) |
3. Даны координаты вершин пирамиды А1А2А3А4. Средствами векторной алгебры найти:
1) угол между ребрами А1А2 и А1А4;
2) площадь грани А1А2А3;
3) объем пирамиды А1А2А3А4;
4) уравнение плоскости основания пирамиды А2А3А4;
5) уравнение высоты пирамиды, проведенной из вершины А1.
| Варианты | 03 | 13 | 23 | 33 | 43 |
| А1(x1;y1;z1) А2(x2;y2;z2) А3(x3;y3;z3) А4(x4;y4;z4) | (2, -1, 2) (8,-8,-4) (-1,-7,4) (8,-7,-5) | (-5, 2, 1) (-1, 3,-7) (-9,-6, 2) (-7, 5,-5) | (-6, 8, 2) (-2, 6,-2) (-6, 4,-1) (-4, 8, 2) | (-3,-2,-3) (5,-6,-4) (-7, 2, 4) (-9, 1,-5) | (8, 3, 3) (6,-3, 6) (2, 9,-4) (4,-5, 2) |
| Варианты | 53 | 63 | 73 | 83 | 93 |
| А1(x1;y1;z1) А2(x2;y2;z2) А3(x3;y3;z3) А4(x4;y4;z4) | (-4, 3,-1) (-6, 4,-3) (-4, 3,9) (-4, 7,-1) | (3,-1,2) (7, 6, 6) (1, 3, 6) (4,-5,-6) | (-2, 3, 3) (-1, 5, 1) (-8, 5, 6) (-8, 6, 5) | (-1,-1,-3) (-6,-1,-3) (3,-9,-4) (2, 5,-1) | (-5,-5, 1) (-5,-5, 9) (-7,-9, 5) (2, 1,-5) |
4. Построить поверхность, определяемую заданным уравнением
| Варианты | Уравнение поверхности |
| 03 | x2 +2x +y2 –2y –2z = 2 |
| 13 | 4x2 –8x –9y2 –36y –72z2 = –184 |
| 23 | x2 -6x + 4y2 +16y + 9 = 0 |
| 33 | x2 + y2 –2z = 1 |
| 43 | x +y2 = 4 |
| 53 | x2 -4x +y2 +2y = z |
| 63 | 4x2 –4x –9y2 –6y = z |
| 73 | x2+6x+2y2–18y–8z = –49 |
| 83 | 6y +4z +20 = z2 |
| 93 | y2 +z2 + 2z = 0 |
Вариант 4
1. Решить систему линейных уравнений методом Гаусса
| Варианты | Варианты | ||
| 04 | 2x -y + 3z -2u = 1 x - z + 2u = 6 x + y - z + u = 4 3x - y + z - u = 0 | 54 | 4x +2y +3z +2u = 5 3x +3y +5z -u = 3 -5x -6y -6z-u = -9 -2x-3y -z -2u = -6 |
| 14 | 3x + 2z + u = –5 –4x–3y +5z–2u =–1 –2x–4y+6z+u = 4 –x–3y+ 7z – u =–6 | 64 | 4x +4y –z –2u = 5 –3y +3z –u = 5 –2x –y –z –u = –7 4x +y +2z –3u = 11 |
| 24 | –x +3y +2z+3u = –7 –4x +6y –6z –2u =8 –2x +5y –u = 3 –6x+11y–6z–3u=11 | 74 | -4x+5z +2u = 9 -4x -y –4z -2u =-8 -x +3y -5z +u = -6 -4x -5y +z = 1 |
| 34 | 2y +3z –u = 9 –2x –6y +z +2u =–2 –2x –5y –3z +u =–8 –2x –4y +4z +u = 8 | 84 | x–3y + 4z +2u = –3 –y –5z –3u = 5 2x +2y –z +u = –2 2x +y –6z –2u = 4 |
| 44 | -4x-2y-5z +u = -3 -2x +6y +4z +u = 0 4x -y +6z -2u = -3 -3y +z -u = -6 | 94 | x +y -4z +2u = 7 2x -6y +2u = -8 -x -5y -5z +u = -9 |
2. Даны координаты вершин треугольника АВС. Требуется:
1) вычислить длину стороны ВС;
2) составить уравнение стороны ВС;
3) вычислить длину высоты, проведенной из вершины А;
4) составить уравнение этой высоты.
| Варианты | 04 | 14 | 24 | 34 | 44 |
| А(x1;y1;) В(x2;y2;) С(x3;y3;) | (-17,-9) (-3,-6) (3,-14) | (12,-13) (-13, 12) (-19, 20) | (-3, 11) (11, 8) (-7,-16) | (0,11) (13, 12) (10, 16) | (-7, 6) (20,-3) (14,-11) |
| Варианты | 54 | 64 | 74 | 84 | 94 |
| А(x1;y1;) В(x2;y2;) С(x3;y3;) | (5, 12) (-5,-8) (7, 1) | (15,-19) (17, 20) (-19,-7) | (19, 1) (-17, 3) (19,-12) | (6,-16) (4, 13) (0, 16) | (1, 4) (14,-9) (19, 3) |
3. Даны координаты вершин пирамиды А1А2А3А4. Средствами векторной алгебры найти:
1) угол между ребрами А1А2 и А1А4;
2) площадь грани А1А2А3;
3) объем пирамиды А1А2А3А4;
4) уравнение плоскости основания пирамиды А2А3А4;
5) уравнение высоты пирамиды, проведенной из вершины А1.
| Варианты | 04 | 14 | 24 | 34 | 44 |
| А1(x1;y1;z1) А2(x2;y2;z2) А3(x3;y3;z3) А4(x4;y4;z4) | (-2,-1,2) (1,-7, 4) (-2, 2, 6) (-4, 8, 8) | (-3,-6,-5) (-9,-9, 1) (5,-2,-6) (-5,-8,-4) | (-3,-7,-6) (3,-5, 3) (-1,-1,-3) (-9,-5,-9) | (2,-7,-3) (8,-7, 5) (-4,-10,-9) (-6,-7, 3) | (-4, 1,-2) (-4,-3,-2) (-7, 3, 4) (-5, 1,-2) |
| Варианты | 54 | 64 | 74 | 84 | 94 |
| А1(x1;y1;z1) А2(x2;y2;z2) А3(x3;y3;z3) А4(x4;y4;z4) | (2, 1,-8) (1, 1,-8) (4,-2,-2) (8,-1,-5) | (2, 1,-5) (2, 5,-5) (-2, 5, 2) (-4,-1,-2) | (-4,-6,-3) (2,-9,-9) (-2,-4,-2) (-1,-4,-9) | (9,-1,-5) (6, 5, 1) (5,-4,-5) (7, 3,-9) | (-4,-5, 4) (-4,-5,-8) (-5,-7, 2) (5,-7, -2) |
4. 1) Составить уравнение поверхности, образованной вращением линии вокруг оси ОZ.
2) Подобрать значение параметра p так, чтобы точка А(x0;y0;z0) лежала на поверхности.
3) Сделать схематический чертёж.
| Варианты | Данные | задачи |
| Уравнение линии в плоскости Х = 0 | А(x0;y0;z0) | |
| 04 | y 2 - 2 = z 2 | (3; -2; 3) |
| 14 | рy 2 + z2 = 4 | (1; 2; 1) |
| 24 | у 2 + 2 = pz 2 | (1; 0; 1) |
| 34 | рy 2 = z 2 | (2; 2; -2) |
| 44 | p + y 2 = z 2 | (-1; 1; 2) |
| 54 | 5y 2 + pz 2 = 10 | (-1; 1; -1) |
| 64 | у 2 + z 2 = p | (-2; 1; 1) |
| 74 | рy 2 + z 2 = 4 | (-1; 1; 0) |
| 84 | рy 2 = z 2 | (3; 2; 3) |
| 94 | рy 2 +4 = z 2 | (-5; 2; 1) |
Вариант 5
1. Решить систему линейных уравнений методом Гаусса
| Варианты | Варианты | ||
| 05 | -x -5y +2u = -4 4x +y -3z -u = -2 x +4y +4z +u = 0 -y +4z +3u = -4 | 55 | -3x -5y -z -3u = 8 -5x +y -4z -u = 5 -4x +y -4z -u = 4 -7x-4y-5z-4u = 12 |
| 15 | 5y -z +3u = 9 -x -y -4z +u = 6 2x -2y -2z -2u = 0 -x+4y-5z+4u =-15 | 65 | 3x +y +u = -9 x +3y -z +2u = -3 x +3y -z +2u = -3 4x +4y-z +3u = -12 |
| 25 | 4x -4y -z +u = -4 -3x+2y-3z+2u =-9 -5x +2y +2u = -1 x-2y -4z +3u = -13 | 75 | 2x -z +2u = -9 -3x+4y+6z+2u =-5 -2x +4y +4z -u = 0 -5x+8y+10z+u =-5 |
| 35 | -3x -y +z +2u = 7 -4x -3y -3z-u = -8 -3x-2y +2z -2u = 2 -7x-4y-2z +u = -1 | 85 | 2x +y -2z -u = 0 -2x -3y +2 u = -1 -3x-2y+2z +u = -2 -2y -2z +u = -1 |
| 45 | 4x -2y +4z -u = 0 x +3y +4z +2u = -2 -x +5y +z -2u = 6 5x +y +8z +u = -2 | 95 | -3x+3y-2z+2u =-3 -x -2y +4z -2u = 6 2x +3y -5z -u = -7 x +y -z -3u = -1 |
2. Даны координаты вершин треугольника АВС. Требуется:
1) вычислить длину стороны ВС;
2) составить уравнение стороны ВС;
3) вычислить длину высоты, проведенной из вершины А;
4) составить уравнение этой высоты.
| Варианты | 05 | 15 | 25 | 35 | 45 |
| А(x1;y1;) В(x2;y2;) С(x3;y3;) | (19, 7) (16, 18) (10, 10) | (13,-3) (-10, 8) (2, 13) | (1,-2) (3,-18) (-9,-13) | (-15, 11) (-18,-11) (12, 5) | (19,-4) (-6,-19) (-9,-15) |
| Варианты | 55 | 65 | 75 | 85 | 95 |
| А(x1;y1;) В(x2;y2;) С(x3;y3;) | (-11, 3) (15, 10) (-5, -5) | (-2, -19) (2, -7) (-6, -1) | (-18, 17) (5, 16) (-10,-4) | (17, 0) (-2,-18) (-11,-6) | (-14, 4) (-15, 7) (-3, 16) |
3. Даны координаты вершин пирамиды А1А2А3А4. Средствами векторной алгебры найти:
1) угол между ребрами А1А2 и А1А4;
2) площадь грани А1А2А3;
3) объем пирамиды А1А2А3А4;
4) уравнение плоскости основания пирамиды А2А3А4;
5) уравнение высоты пирамиды, проведенной из вершины А1.
| Варианты | 05 | 15 | 25 | 35 | 45 |
| А1(x1;y1;z1) А2(x2;y2;z2) А3(x3;y3;z3) А4(x4;y4;z4) | (9,-3,3) (2,3,9) (-2,-3,3) (7,-7,7) | (2,-5,1) (-4,-3,10) (2,-5,-5) (-4,-8,-1) | (3,5,-5) (7,-3,-6) (-3, 8, 1) (9,-1,-2) | (-5, 5, 4) (-5, 5,-4) (-7, 9, 8) (-3,-4,-2) | (8,-4, 3) (8,-7, 3) (8,-4, 6) (5, 2,-3) |
| Варианты | 55 | 65 | 75 | 85 | 95 |
| А1(x1;y1;z1) А2(x2;y2;z2) А3(x3;y3;z3) А4(x4;y4;z4) | (-2,-2,-2) (-3,-4,-4) (-2,-6,-2) (-2,-6,-5) | (-5,-3,-1) (2, 1, 3) (-6, 1, 7) (-4,-7, 7) | (1, 2, 6) (-5,-4, 3) (-1, 4, 7) (9, 6, 7) | (-1,-5, 9) (1,-9, 5) (-7,-8, 3) (1,-4, 7) | (-7, 4,-7) (-7, 4,-1) (-3,-4,-6) (-1,-2,-4) |
4. Построить поверхность, определяемую заданным уравнением
| Вариант | Уравнение поверхности |
| 05 | -4x +y2 -6y + 17 = 0 |
| 15 | у 2 - 2y + z2 = 0 |
| 25 | x2-6x+4y2+9z2+36z= 99 |
| 35 | 16x2+3y2 +16z2 -48 = 0 |
| 45 | 2x2 +y2 +4y +2z2 = 4x-4z-7 |
| 55 | x2 -9y2 -3z2 = 0 |
| 65 | х2 +4y2 -2z2 = 0 |
| 75 | x2+2x+2y2+4y+4z2+1= 0 |
| 85 | x2 +y2 +2z2 -2 -4z = 0 |
| 95 | 9x2-18x+16y2+64y+36z2-216z +253= 0 |
Вариант 6
1. Решить систему линейных уравнений матричным методом и по формулам Крамера
| Варианты | &
Воспользуйтесь поиском по сайту:  ©2015 - 2026 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...
|

