 |
Задания для самостоятельного выполнения
|
|
|
|
Задача 1. Порядок выступления 8 участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?
Задача 2. Расписание одного дня состоит из 4 дисциплин. Определить количество вариантов расписания при выборе из 15 дисциплин.
Задача 3. В шахматном турнире участвуют 12 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?
Задача 4. Из 25 студентов 5 имеют спортивные разряды. Какова вероятность того, что выбранные наудачу 2 студента – разрядники?
Задача 5. Среди 1000 новорожденных оказалось 487 девочек. Найти относительную частоту рождения девочек.
Задача 6. На отрезке L длины 30 см помещен меньший отрезок l = 15 см. Найти вероятность того, что точка наудачу поставленная на больший отрезок, попадет также и на меньший отрезок. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.
Задача 7. Вероятность того, что студент сдаст первый экзамен, равна 0,9; второй – 0,8; третий – 0,7. Найти вероятность того, что студентом будут сданы: а) только первый экзамен;  б) только один экзамен; в) три экзамена; г) по крайней мере два экзамена; д) хотя бы один экзамен.
б) только один экзамен; в) три экзамена; г) по крайней мере два экзамена; д) хотя бы один экзамен.
Задача 8. Среди 1000 лотерейных билетов 25 выигрышных. Найти вероятность того, что два наудачу выбранные билета окажутся выигрышными.
Задача 9. В торговую фирму поступили телевизоры от трех поставщиков в отношении 1:4:5. Практика показала, что телевизоры поступающие от 1-го, 2-го и 3-го поставщиков, не потребуют ремонта в течение гарантийного срока в 98%, 88% и 92% случаев.
1) Найти вероятность того, что поступивший в торговую фирму телевизор не потребует ремонта в течение гарантийного срока.
|
|
|
2) Проданный телевизор потребовал ремонта в течение гарантийного срока. От какого поставщика вероятнее всего поступил этот телевизор?
Задача 10. В среднем 20% пакетов акций на аукционах продаются по первоначально заявленной цене. Найти вероятность того, что из 8 пакетов акций в результате торгов по первоначально заявленной цене: 1) будет продано 2 пакета; 2) не будут проданы 5 пакетов.
Задача 11. По результатам проверок налоговыми инспекциями установлено, что в среднем каждое второе частное предприятие региона имеет нарушение финансовой дисциплины. Найти вероятность того, что из 100 зарегистрированных в регионе частных предприятий имеют нарушения финансовой дисциплины: а) 48 предприятий; б) от 48 до 55.
Задача 12. Завод отправил на базу 10000 стандартных изделий. Среднее число изделий, повреждаемых при транспортировке составляет 0,02%. Найти вероятность того, что из 10000 изделий будет повреждено три изделия.
Задача 13. Дискретная случайная величина Х задана законом распределения
| Х | |||
| Р | 0,3 | 0,5 | 0,2 |
Найти функцию распределения 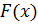 и построить ее график.
и построить ее график.
Задача 14. Случайная величина Х задана функцией распределения

Вычислить вероятности попадания СВ Х в интервалы (1,5; 2,5) и (2,5; 3,5).
Задача 15. Случайная величина Х задана функцией распределения
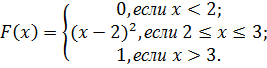
Найти плотность распределения СВ Х.
Задача 16. СВ Х подчинена закону распределения с плотностью f(x), причем

Требуется: 1) найти коэффициент а; 2) найти вероятность попадания Х в промежуток (1; 2).
Задача 17. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение СВ Х, заданной законом распределения:
| Х | -5 | -2 | |||
| р | 0,2 | 0,1 | 0,3 | 0,15 | 0,25 |
Задача 18. СВ Х в интервале (0; 4) задана плотностью распределения 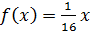 , вне этого интервала
, вне этого интервала 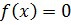 . Найти дисперсию Х.
. Найти дисперсию Х.
Образцы решения заданий
Задание 1. Сколько существует способов распределить три премии между десятью сотрудниками отдела: а) одинакового размера; б) разных размеров; в) одинакового размера, если сотрудники могут быть премированы за различные показатели и более одного раза; г) разного размера, если сотрудники могут быть премированы за различные показатели и более одного раза?
|
|
|
Решение. Каждому работнику отдела поставим в соответствие некоторый номер – 1, 2, …, 10. Тогда любая тройка номеров из этого списка соответствует одному варианту распределения премий. Условимся также премии располагать слева направо в порядке убывания, когда они различаются по размеру.
а) если премии одинакового размера, то наборы номеров, например, (1, 2, 3); (1, 3, 2); (2, 1, 3); (2, 3, 1) неразличимы (они соответствуют факту награждения первых трёх сотрудников по списку). Поэтому здесь важен только состав, порядок расположения элементов в наборе роли не играет. Значит, способов распределить три премии одинакового размера столько же, сколько сочетаний «из 10 по 3»,  .
.
б) если премии разного размера, то наборы номеров, например, (1, 2, 3); (1, 3, 2) разные (для 2-го и 3-го сотрудников). Поэтому здесь важен не только состав, но и порядок расположения элементов в наборе. Значит, способов распределить три премии разного размера столько же, сколько размещений «из 10 по 3», 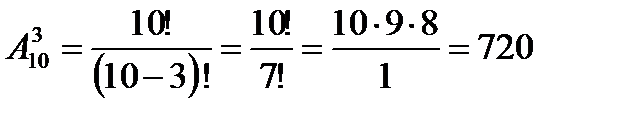 .
.
в) если премии одинакового размера, а сотрудники могут быть премированы и более одного раза, то наборы номеров, например, (1, 1, 3); (1, 3, 1) неразличимы. В обоих случаях 2 премии получил работник с № 1 и 1 премию – работник № 3. Значит, способов распределить три премии одинакового размера в этом случае столько же, сколько существует сочетаний с повторениями «из 10 по 3»,  .
.
г) если премии разного размера, а сотрудники могут быть премированы и более одного раза, то наборы номеров, например, (1, 1, 3); (1, 3, 1) различные. В первом варианте 1-й работник имеет премию максимальную и 2-ю по величине, во 2-м варианте 1-й работник имеет премию максимальную и 3-ю по величине. Значит, наборы представляют собой размещения с повторениями. Поэтому способов распределить три премии разного размера в столько же, сколько существует размещений с повторениями «из 10 по 3», 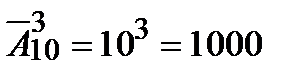 .
.
Задание 2. Сколько трехзначных чисел можно составить из множества цифр {1,2,3,4,5,6}
|
|
|
а) без повторений; б) с повторениями?
Решение. а) Так как числа 123 и 321 разные, то порядок расположения внутри набора существенен. Поэтому чисел можно составить столько, сколько будет размещений «из 6 по 3», 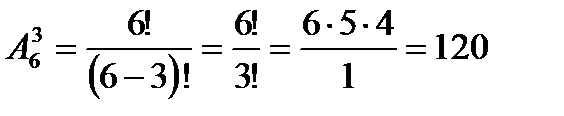 .
.
б) Если цифры повторяются, то важен и состав, и порядок в наборе. Поэтому чисел можно составить столько, сколько будет размещений с повторениями «из 6 по 3», то есть 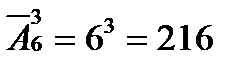 .
.
Задание 3. В отделении банка работают 25 человек, 10 из них мужчины. Для перевода в другое отделение банка необходимо отобрать 5 сотрудников. Какова вероятность того, что среди отобранных сотрудников три женщины?
Решение. Пусть событие A означает, что из 5 отобранных для перевода в другое отделение сотрудников три женщины. Тогда
 .
.
Общее число n способов выбора 5 сотрудников из 25 равно числу сочетаний из 25 по 5, т.е.  . Определим число m, благоприятствующих событию А исходов — «среди отобранных 5 сотрудников будут 3 женщины». Число способов выбрать 3 женщины из 15 равно
. Определим число m, благоприятствующих событию А исходов — «среди отобранных 5 сотрудников будут 3 женщины». Число способов выбрать 3 женщины из 15 равно  . Каждому такому выбору соответствует
. Каждому такому выбору соответствует 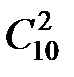 способов выбора 2-х мужчин из 10. Следовательно,
способов выбора 2-х мужчин из 10. Следовательно, 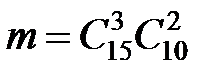 . Тогда
. Тогда
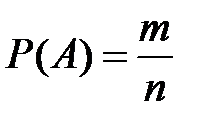 =
= 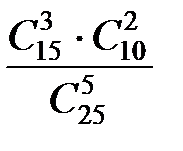 =
=  =
=  =
= 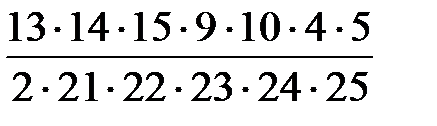 =
= 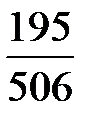
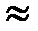 0,38.
0,38.
Ответ: 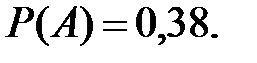
Задание 5. В течение года три фирмы независимо друг от друга могут обанкротиться (прекратить функционирование) с вероятностями 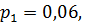
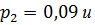
 = 0,08 соответственно. Вычислить вероятность того, что в течение года будут функционировать:
= 0,08 соответственно. Вычислить вероятность того, что в течение года будут функционировать:
а) только две фирмы;
б) хотя бы одна фирма;
в) не более одной фирмы.
Решение
Пусть 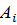 , i=1, 2, 3 – события, означающие банкротство каждой из трёх фирм. Тогда P(
, i=1, 2, 3 – события, означающие банкротство каждой из трёх фирм. Тогда P(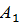 ) = 0,06, P(
) = 0,06, P(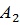 ) = 0,09, P(
) = 0,09, P(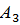 ) = 0,08; P(
) = 0,08; P(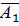 ) =0,94, P(
) =0,94, P( ) = = 0,91, P(
) = = 0,91, P(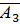 ) = 0,92. Здесь
) = 0,92. Здесь 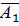 ,
,  ,
, 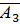 – противоположные относительно
– противоположные относительно 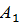 ,
, 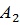 ,
, 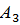 случайные события.
случайные события.
а) Рассмотрим событие В= 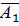
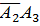 +
+ 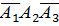 +
+ 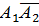
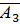 . Оно заключается в том, что в течение года не обанкротятся только две фирмы.
. Оно заключается в том, что в течение года не обанкротятся только две фирмы.
Так как 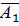
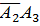 ,
, 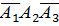 ,
, 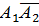
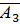 несовместны и
несовместны и 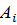 (i=1, 2, 3) независимы, то на основании теорем сложения и умножения вероятностей получим:
(i=1, 2, 3) независимы, то на основании теорем сложения и умножения вероятностей получим:
Р(В)= Р(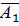 ) Р(
) Р( ) Р(
) Р(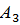 ) + Р(
) + Р(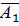 ) Р(
) Р(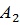 ) Р(
) Р(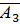 ) + Р(
) + Р(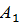 ) Р(
) Р( ) Р(
) Р(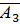 )= =0,94∙0,91∙0,08+0,94∙0,09∙0,92+0,06∙0,91∙0,92=0,196496≈0,1965.
)= =0,94∙0,91∙0,08+0,94∙0,09∙0,92+0,06∙0,91∙0,92=0,196496≈0,1965.
б) Обозначим через С событие, состоящее в том, что все три фирмы в течение года обанкротятся. Тогда
Р(С)=Р(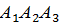 )= Р(
)= Р(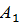 ) Р(
) Р(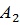 )Р(
)Р(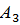 )=0,06∙0,09∙0,08=0,000432.
)=0,06∙0,09∙0,08=0,000432.
Вероятность того, что хотя бы одна фирма не обанкротится, равна
|
|
|
1– Р(С)=1–0,000432=0,999568≈0,9996.
в) Пусть теперь D – случайное событие, состоящее в том, что в течение года будет функционировать не более одной фирмы. Оно означает, что либо все три фирмы обанкротятся, либо будет функционировать только одна фирма. Тогда D= 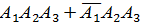 +
+ 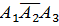 +
+ 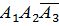 и
и
Р(D) = Р(С)+ Р(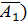 Р(
Р( Р(
Р(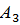 ) + Р(
) + Р(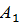 ) Р(
) Р( )Р(
)Р(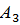 ) + Р(
) + Р(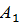 )Р(
)Р( Р(
Р(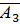 ) = =0,000432+0,94∙0,09∙0,08+0,06∙0,91∙0,08+0,06∙0,09∙0,92=0,016536≈0,0165.
) = =0,000432+0,94∙0,09∙0,08+0,06∙0,91∙0,08+0,06∙0,09∙0,92=0,016536≈0,0165.
Ответ: а) 0,1965; б) 0,9996; в)0,0165.
Задание 6. В магазине имеются холодильники, произведенные двумя заводами в количественном соотношении 2:9. Вероятность выхода из строя в течение гарантийного срока холодильника, произведенного первым заводом, равна 0,005, а вторым – 0,009. Купленный в магазине холодильник выдержал гарантийный срок. Вычислить вероятность того, что этот холодильник произведен вторым заводом.
Решение
Пусть А– событие, состоящее в том, что холодильник выдержит гарантийный срок, 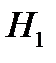 и
и 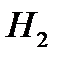 – гипотезы, состоящие в том, что он произведен первым или вторым заводом соответственно. Тогда
– гипотезы, состоящие в том, что он произведен первым или вторым заводом соответственно. Тогда
 ;
; 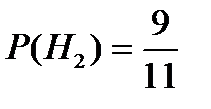 .
.
Из условия задачи следует, что: 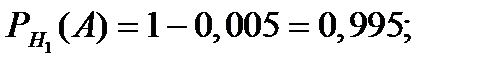
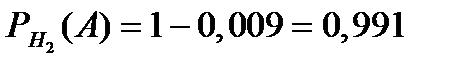 .
.
Вероятность того, что холодильник, выдержавший гарантийный срок, произведен вторым заводом, т.е.  вычислим по формуле Бейеса:
вычислим по формуле Бейеса: 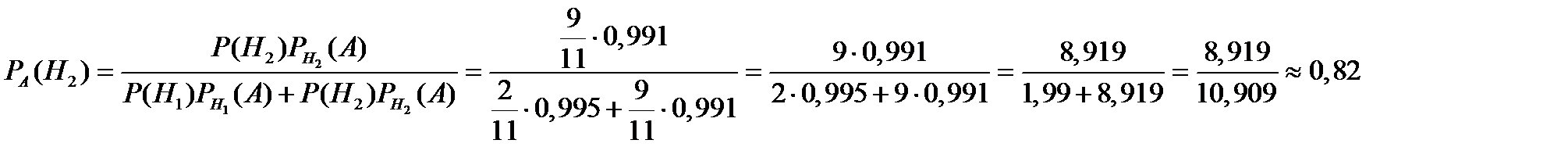 Ответ: 0,82.
Ответ: 0,82.
Задание 7. При проведении социологического опроса студентов каждый из них, независимо друг от друга, может дать неискренний ответ с вероятностью 0,12. Вычислить вероятность того, что из 300 ответов неискренних будет:
а) ровно 30;
б) не более 70;
в) не менее 30 и не более 70.
Решение
а) Так как число опрошенных студентов 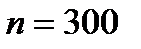 достаточно велико, а вероятность
достаточно велико, а вероятность 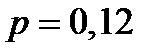 сравнительно мала, то воспользуемся локальной теоремой Муавра–Лапласа:
сравнительно мала, то воспользуемся локальной теоремой Муавра–Лапласа:
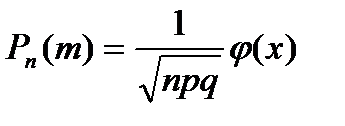 , где
, где  .
.
В нашем случае 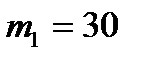 ,
,  ,
,
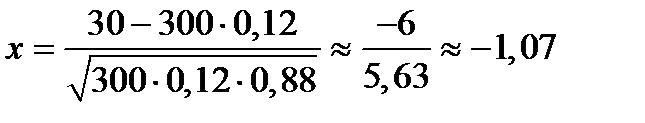
Функция 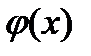 четная, поэтому
четная, поэтому  (– 1,07)=
(– 1,07)=  (1,07). По таблице [3, Приложение 1] найдем
(1,07). По таблице [3, Приложение 1] найдем  (1,07) = 0,2251. Искомая вероятность
(1,07) = 0,2251. Искомая вероятность 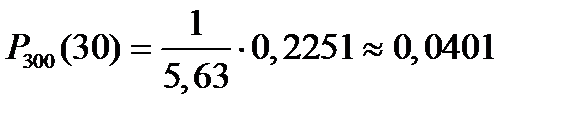 .
.
б) Требование, чтобы неискренних ответов было не более 70, означает, что их число может быть равно 0, 1,2,…,70. Таким образом, в рассматриваемом случае следует принять 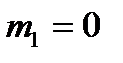 ,
, 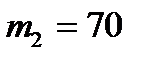 и воспользоваться интегральной теоремой Муавра–Лапласа, по которой
и воспользоваться интегральной теоремой Муавра–Лапласа, по которой 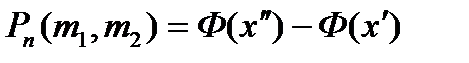 , где
, где  – функция Лапласа,
– функция Лапласа, 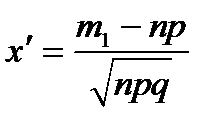 ;
;  .
.
Вычислим 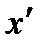 и
и 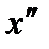 :
:
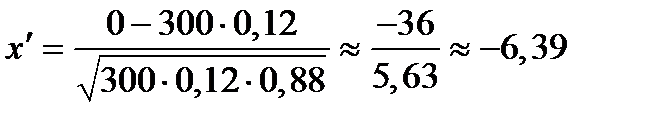 ;
; 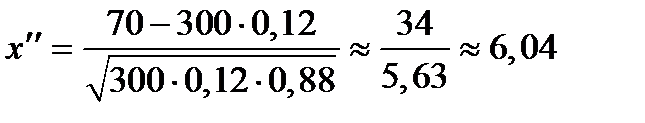 .
.
Учитывая, что функция Лапласа нечетная, т.е. 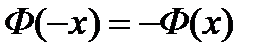 , используя таблицу значений
, используя таблицу значений  [3,Приложение 2], получим
[3,Приложение 2], получим
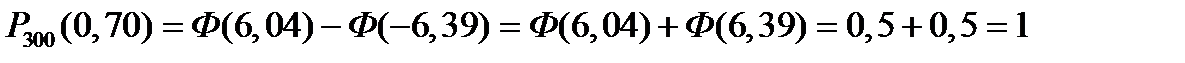 .
.
Для значений  полагают
полагают  .
.
в) В этом пункте нужно вычислить 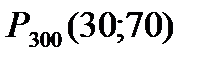 , т.е. вероятность того, что из ответов трехсот опрошенных студентов неискренних будет не менее 30 и не более 70. Вычислим
, т.е. вероятность того, что из ответов трехсот опрошенных студентов неискренних будет не менее 30 и не более 70. Вычислим  и
и  :
:
 ;
; 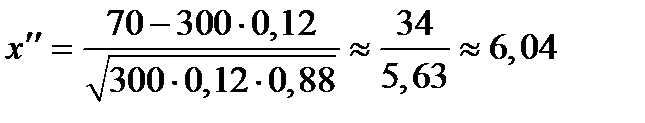 .
.
Следовательно,

Ответ: а) 0,0401; б) 1; в) 0,8577.
Задание 8. Два товароведа проверяют партию изделий на качество. Производительности их труда относятся как 5: 4.Вероятность выявления брака первым товароведом составляет 85 %, вторым – 90 %. Из проверенных изделий отбирают три. Составить закон распределения случайного числа  – годных изделий среди отобранных. Вычислить математическое ожидание
– годных изделий среди отобранных. Вычислить математическое ожидание 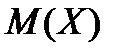 , дисперсию
, дисперсию 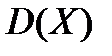 и среднее квадратическое отклонение σ (Х).
и среднее квадратическое отклонение σ (Х).
|
|
|
Решение
Из условия задачи следует, что  – дискретная случайная величина, возможными значениями которой являются числа
– дискретная случайная величина, возможными значениями которой являются числа 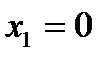 ,
,  ,
, 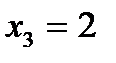 ,
, 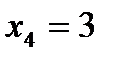 .
.
Так как имеют место оба условия схемы Бернулли, вероятности их появления будем вычислять по формуле Бернулли  .
.
Пусть А– случайное событие, состоящее в том, что каждое изделие из трех отобранных для проверки окажется годным; 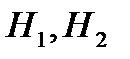 – гипотезы, заключающиеся в том, что оно проверено первым или вторым товароведом соответственно. Тогда по формуле полной вероятности
– гипотезы, заключающиеся в том, что оно проверено первым или вторым товароведом соответственно. Тогда по формуле полной вероятности
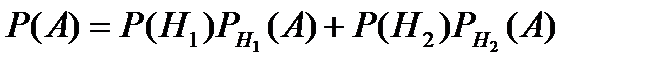 .
.
По условию 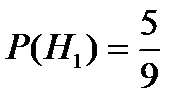 ,
,  ,
, 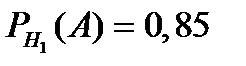 ,
, 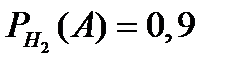 .
.
Значит, 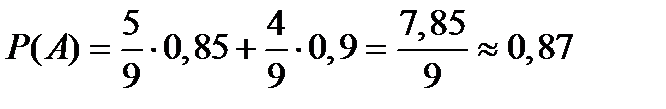 .
.
Итак, для вычисления вероятностей возможных значений случайной величины 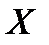 по формуле Бернулли
по формуле Бернулли 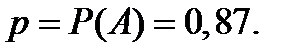

Тогда
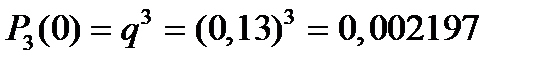 ;
;  ;
;
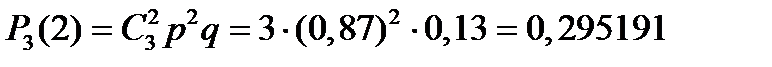 ;
; 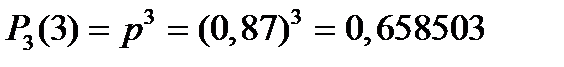 .
.
Контроль: 0,002197+0,044109+0,295191+0,658503 = 1.
Закон распределения случайной величины 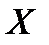 имеет вид:
имеет вид:
Таблица 4.1
| X | ||||
| P | 0,002197 | 0,044109 | 0,295191 | 0,658503 |
Найдем математическое ожидание, дисперсию и среднее квадратическое отклонение.
По определению 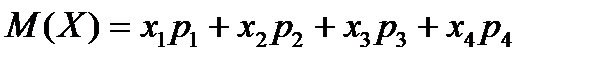 .
.
Значит,  .
.
По формуле 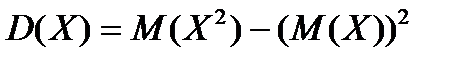 вычислим дисперсию.
вычислим дисперсию.
 .
.
Среднее квадратическое отклонение 
Замечание. Рассмотренная в задаче случайная величина Х – дискретная и распределена по биномиальному закону. Поэтому математическое ожидание и дисперсию можно вычислить так:
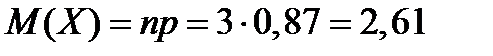 ;
;  .
.
Задание 9. Вероятность того, что при составлении бухгалтерского баланса не допущена ошибка, равна 0,9. Аудитору на заключение представлено 4 баланса предприятия. Составьте закон распределения случайной величины Х – числа положительных заключений на проверяемые балансы. Найдите:
1) числовые характеристики этого распределения: М(Х), D(X);
2) функцию распределения F(X) и постройте ее график;
3) вероятность того, что:
а) ни один бухгалтерский баланс не получит положительного заключения;
б) хотя бы один бухгалтерский баланс получит положительное заключение;
в) не более двух бухгалтерских балансов получат положительное заключение.
Решение. Составим закон распределения случайной величины Х – числа положительных заключений на проверяемые балансы. Из четырех проверяемых балансов положительное заключение может получить ни один баланс, один, два, три и все четыре баланса, т.е.
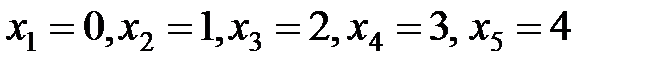 .
.
Вероятности вычислим по формуле Бернулли  , при этом
, при этом 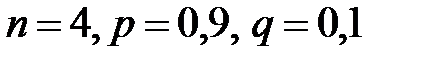 .
.
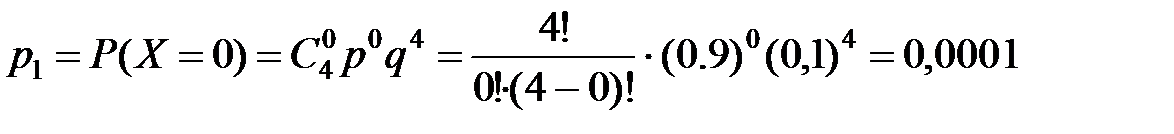 ;
;
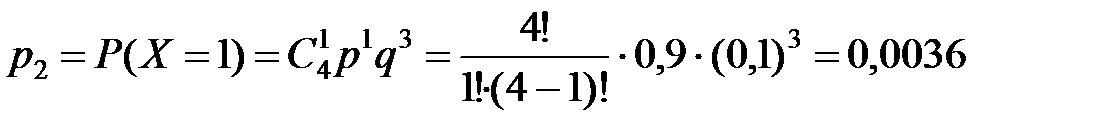 ;
;
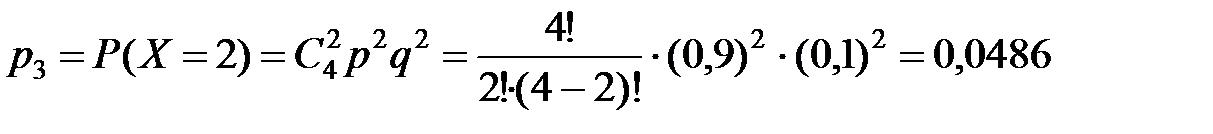 ;
;
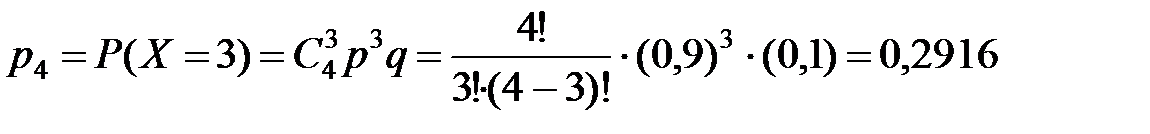 ;
;
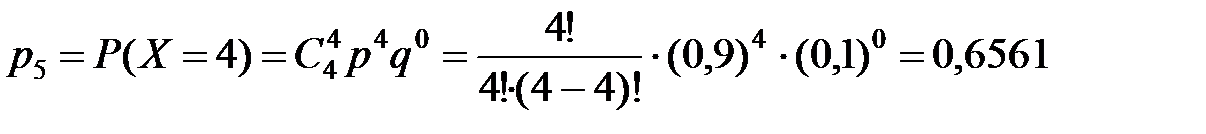 .
.
Проверим выполнение соотношения 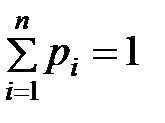 .
.
 .
.
Тогда ряд распределения случайной величины Х – числа положительных заключений на проверяемые балансы примет вид
Таблица 4.2
| Х | |||||
| р | 0,0001 | 0,0036 | 0,0486 | 0,2916 | 0,6561 |
1) Найдём математическое ожидание 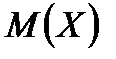 .
.
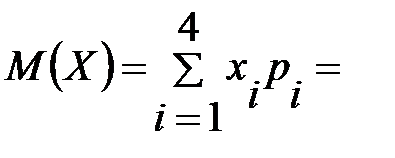
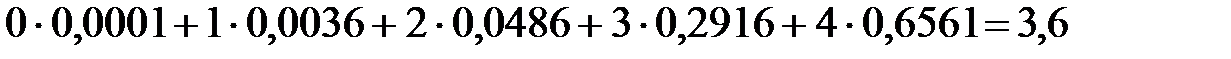
Найдём дисперсию 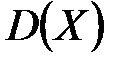 .
.
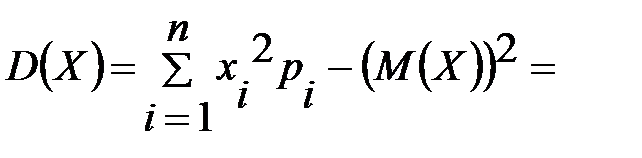
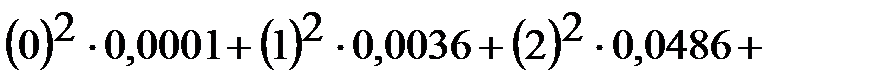
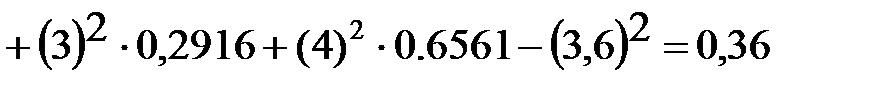 .
.
Замечание. Так как случайная величина Х имеет биномиальное распределение, то числовые характеристики можно вычислять по формулам:
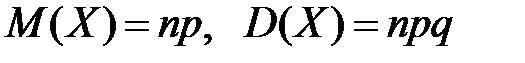 .
.
2) Найдём функцию распределения 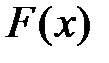 .
.

или

Построим график функции  .
.
Рисунок 4 – График функции 
3) Искомые вероятности найдем, используя закон распределения СВ Х:
а) р (Х = 0)= 0,0001;
б) р (Х ≥ 1) = р (Х = 1) + р (Х = 2) + р (Х = 3) + р (Х = 4) =
= 0,0036 + 0,0486 + 0,2916 + 0,6561 = 0,9999,
Или
р (Х ≥ 1) = 1 – р (Х = 0) = 1 – 0,0001 = 0,9999.
в) р (Х £ 2) = р (Х = 0) + р (Х = 1) + р (Х = 2) =
= 0,0001 + 0,0036 + 0,0486 = 0,0523.
Ответ: 1) 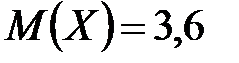 ;
;  ; 3) а) 0,0001; б) 0,9999; в) 0,0523.
; 3) а) 0,0001; б) 0,9999; в) 0,0523.
Задание 10. Дана функция распределения СВ Х:
F (x) = 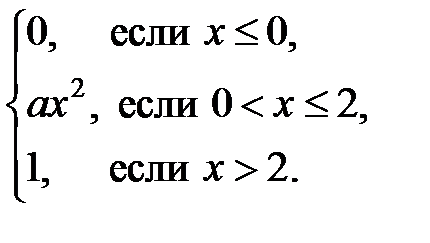
Найти:
1) коэффициент а;
2) математическое ожидание М (Х), дисперсию D (X);
3) Р 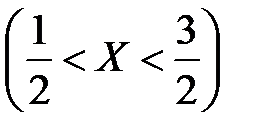 .
.
Построить графики функций F (x) и f (x).
Решение. Найдем вид функции плотности распределения вероятностей заданной случайной величины.
f (x) = F ′(x) = 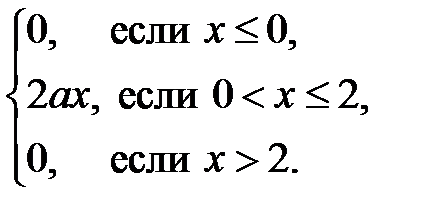
1) Для нахождения значения параметра а используем свойство нормированности функции плотности распределения вероятностей: 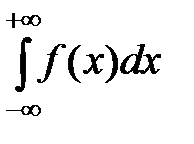 = 1.
= 1.
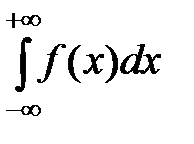 =
=  +
+ 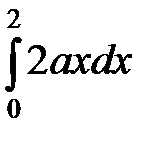 +
+ 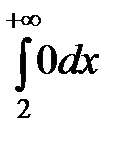 =
= 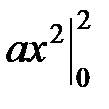 = 4 а = 1,
= 4 а = 1,
откуда, а =  .
.
Таким образом,
F (x) = 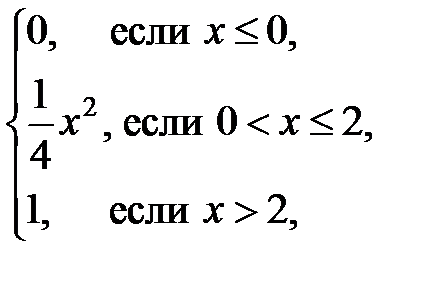 f (x) =
f (x) = 
2) Математическое ожидание М (Х) найдем по формуле:
М (Х) = 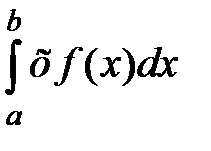 =
= 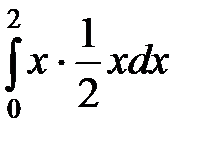 =
= 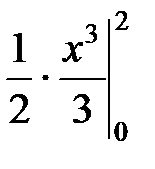 =
=  .
.
Дисперсию D (X) найдем по формуле:
D (X) = 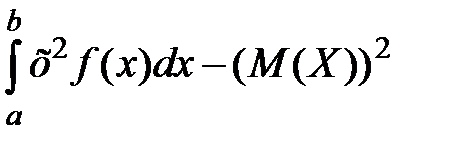 =
=
=  –
– 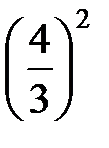 =
=  –
– 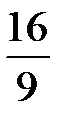 = 2 –
= 2 – 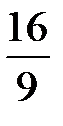 =
= 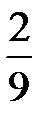 .
.
3) Для нахождения вероятности попадания случайной величины Х в интервал 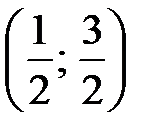 воспользуемся формулой
воспользуемся формулой
P (α ≤ X ≤ β) = F (β) – F (α).
Получим
Р 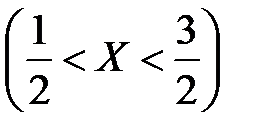 = F
= F 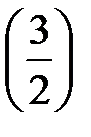 – F
– F 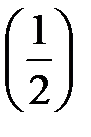 =
=  –
–  =
=  =
= 
Построим графики функций F (x) и f (x) (рисунки 5а, 5б)
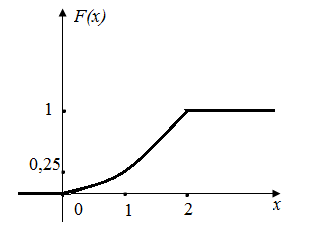
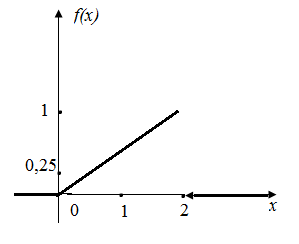
а) б)
Рисунок 5 – Графики функций F (x) и f (x)
Ответ: 1) а = 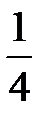 ; 2) М (Х) =
; 2) М (Х) = 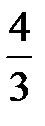 ; D (X) =
; D (X) =  ; 3) Р
; 3) Р 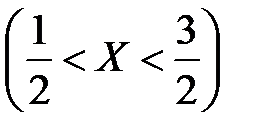 =
=  .
.
|
|
|


