 |
Тема 5. Элементы теории функции комплексной переменной.
|
|
|
|
1.Знать определение функции комплексной переменной и уметь ее геометрически изображать.
2.Уметь находить действительную и мнимую части функции комплексной переменной.
3.Знать определение предела функции комплексной переменной и уметь их вычислять.
4.Знать определение функции непрерывной в точке.
5.Знать определение производной функции комплексной переменной.
6.Знать условия дифференцируемости функции комплексной переменной (условия Коши-Римана).
Задания для самостоятельного выполнения
1 Дана функция  . Найти значения функции при: а)
. Найти значения функции при: а) 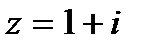 ,
,
б)  , в)
, в)  , г)
, г)  .
.
2 Определить действительную и мнимую части функции  :
:
а)  , б)
, б)  , в)
, в)  .
.
3 Найдите пределы:
а) 



4 Показать, что функция f (z) дифференцируема и найти ее производную.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Образцы решения заданий.
Задание 1. Дана функция  . Найти значения функции при
. Найти значения функции при  .
.
Решение. Имеем
 .
.
Задание 2. Определить действительную и мнимую части функции  .
.
Решение. Определим действительную и мнимую часть функции  , т.е. представим функцию
, т.е. представим функцию  в виде
в виде  .
.
Так как  , то
, то
 = (x + iy)2 +3 i (x + iy) =
= (x + iy)2 +3 i (x + iy) =  =
=
=  .
.
Следовательно,
u (x, y) = x 2 – y 2 - 3 y; v (x, y) = 2 xy + 3 x.
Задание 3. Найдите предел 

Решение. 
Пусть функция  определена в некоторой области
определена в некоторой области  комплексного переменного
комплексного переменного  .Пусть точки
.Пусть точки  и
и  принадлежат области
принадлежат области  . Приращение функции w в точке z:
. Приращение функции w в точке z:
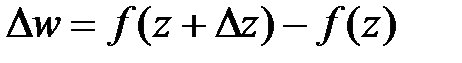 , где
, где  .
.
Производной 
 функции
функции  в точке
в точке  называется предел отношения
называется предел отношения  при
при 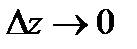
 ,
,
если он существует и конечен.
Если существует производная  , то функция
, то функция  называется дифференцируемой в точке z.
называется дифференцируемой в точке z.
Пусть  , тогда
, тогда  и в каждой точке дифференцируемости функции
и в каждой точке дифференцируемости функции  выполняются соотношения:
выполняются соотношения:
 ,
,  .
.
Эти соотношения называются условиями Коши-Римана.
Обратно, если в некоторой точке  выполняются условия Коши-Римана и, кроме того, функции
выполняются условия Коши-Римана и, кроме того, функции  и
и  дифференцируемы как функции двух действительных переменных, то функция
дифференцируемы как функции двух действительных переменных, то функция  является дифференцируемой в точке, как функция комплексного переменного
является дифференцируемой в точке, как функция комплексного переменного  .
.
|
|
|
Задание 4. Показать, что функция f (z) = iz 3 + z 2 – 3 iz дифференцируема.
Решение. Определим действительную и мнимую часть функции f (z) = iz 3 + z 2 – 3 iz, т.е. представим функцию  в виде
в виде  .
.
Так как  , то
, то
f (z) = iz 3 + z 2 – 3 iz = i (x + iy)3 + (x + iy)2 – 3 i (x + iy) =
= i (x 3 + 3 x 2 yi – 3 xy 2 – y 3 i) + x 2 + 2 xyi – y 2 – 3 x i + 3 y =
= x 3 i – 3 x 2 y – 3 xy 2 i + y 3 + x 2 + 2 xyi – y 2 – 3 xi + 3 y =
= (y3 + x 2 – y 2 – 3 x 2 y + 3 y) + i (x 3 – 3 xy 2 + 2 xy – 3 x).
Следовательно,
u (x, y) = y3 + x 2 – y 2 – 3 x 2 y + 3 y; v (x, y) = x 3 – 3 xy 2 + 2 xy – 3 x.
Проверим выполнение условий Коши–Римана:
 ,
,  .
.
Найдем частные производные функций u (x, y) и v (x, y):

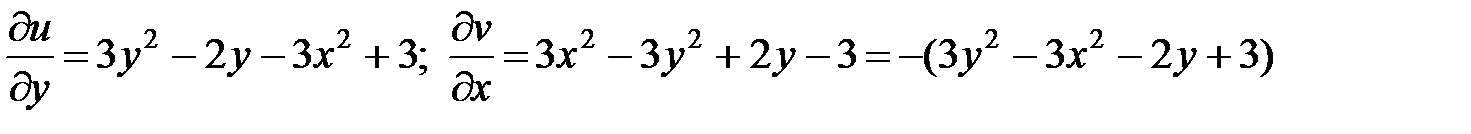 .
.
Условия Коши-Римана выполняются при всех значениях х и у, следовательно, функция f (z) = iz 3 + z 2 – 3 iz является дифференцируемой на всей комплексной плоскости.
Тема 6. Элементы операционного исчисления.
1.Знать определения оригинала и изображения. Изображения некоторых функций.
2.Используя таблицу основных формул соответствия и теоремы операционного исчисления, уметь находить изображения оригиналов и оригиналы по их изображениям.
3.Уметь находить изображения дифференциального выражения.
4.Уметь находить операционным методом частные решения дифференциальных уравнений с постоянными коэффициентами.
Задания для самостоятельного выполнения
1 Найти изображение F (p) по заданному оригиналу f (t):
а)  ; б)
; б)  ; в)
; в)  .
.
2 Найти оригинал f (t) по изображению F (p):
а)  ; б)
; б)  ;
;
в)  .
.
3 Найти изображение дифференциального выражения:
а)  ;
;
б)  ;
;
в)  .
.
4 Операционным методом найти решение дифференциального уравнения, удовлетворяющего заданным начальным условиям.
а)  ; б)
; б)  .
.
Образцы решения заданий
Любая комплексная функция f (t) действительного переменного t называется оригиналом, если она удовлетворяет следующим условиям:
1) f (t) – кусочно–непрерывная при t ≥ 0, это значит, что она либо непрерывна, либо в каждом конечном интервале имеет лишь конечное число точек разрыва 1-го рода;
|
|
|
2) f (t) ≡ 0 при t < 0;
3) при t → ∞ функция f (t) растёт не быстрее некоторой показательной функции (имеет ограниченную степень роста), т.е. существует такое положительное число М и такое неотрицательное число s, что для всех t ≥ 0 выполняется неравенство:| f (t) | ≤ M ∙ est, М > 0, s ≥ 0.
Точная нижняя грань s 
 тех значений s, для которых выполняется указанное условие, называется показателем ро ста функции f (t).
тех значений s, для которых выполняется указанное условие, называется показателем ро ста функции f (t).
Изображением функции f (t) по Лапласу называется функция F (p) комплексного переменного p=s+i  из некоторой области D плоскости комплексного переменного p, определяемая равенством
из некоторой области D плоскости комплексного переменного p, определяемая равенством
F (p) =  .
.
Связь между функциями f (t)и F (p) будем обозначать в дальнейшем следующим образом: f (t) = L –1{ F (p)} или F (p) = L { f (t)}.
Первую запись следует читать так: «Оригинал f (t) имеет изображение F (p)». Вторую запись следует читать так: «Изображение F (p) имеет оригинал f (t)» или «f (t) является оригиналом изображения F (p)». Используются также и другие обозначения.
|
|
|


