 |
Задания для самостоятельного выполнения.
|
|
|
|
Здесь везде  -номер студента по списку.
-номер студента по списку.
1. Пусть выборка задана таблицей 8. 1. Найти её числовые характеристики.
Таблица 8.1

| -1 
| 0 
| 1 
| 2 
|

|
2. Найти доверительный интервал для неизвестного математического ожидания нормально распределённой генеральной совокупности с надёжностью  при известной генеральной дисперсии
при известной генеральной дисперсии  , выборочном среднем
, выборочном среднем  , найденным по выборке объёма
, найденным по выборке объёма  .
.
3. Найти доверительный интервал для неизвестного математического ожидания нормально распределённой генеральной совокупности при неизвестной генеральной дисперсии с надёжностью  , выборочном среднем
, выборочном среднем  и выборочной дисперсии
и выборочной дисперсии 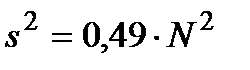 , найденных по выборке объёма
, найденных по выборке объёма  .
.
4. Для проверки эффективности новой технологии отбираются две группы рабочих. В первой группе (где она применяется) численностью  человек средняя выработка
человек средняя выработка  шт.,
шт.,  шт. Эти же показатели для другой группы (без применения новой технологии) численностью
шт. Эти же показатели для другой группы (без применения новой технологии) численностью  человека:
человека:  шт.,
шт.,  шт. На уровне значимости
шт. На уровне значимости 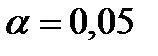 определить, действительно ли новая технология влияет на производительность.
определить, действительно ли новая технология влияет на производительность.
5. При уровне значимости 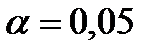 проверить гипотезу о нормальном распределении генеральной совокупности по эмпирическим и теоретическим частотам:
проверить гипотезу о нормальном распределении генеральной совокупности по эмпирическим и теоретическим частотам:
Таблица 8.2

| 6 
| 12 
| 16 
| 40 
| 13 
|
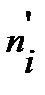
|
Образцы решения заданий.
Задание1. Пусть выборка задана таблицей 8. 3.Найти её числовые характеристики.
Таблица 8.3

| -1 | |||

|
Решение. Выборочная средняя  , выборочная дисперсия
, выборочная дисперсия  , исправленная выборочная дисперсия
, исправленная выборочная дисперсия  , выборочное среднеквадратическое отклонение
, выборочное среднеквадратическое отклонение  , исправленное выборочное среднеквадратическое отклонение
, исправленное выборочное среднеквадратическое отклонение  , выборочная мода
, выборочная мода 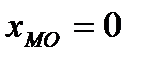 , выборочная медиана
, выборочная медиана  .
.
Задание 2. Найти доверительный интервал для неизвестного математического ожидания нормально распределённой генеральной совокупности с надёжностью  при известной генеральной дисперсии
при известной генеральной дисперсии  , выборочном среднем
, выборочном среднем  , найденным по выборке объёма
, найденным по выборке объёма  .
.
|
|
|
Решение. Искомый доверительный интервал имеет вид:  . Квантиль стандартного нормального распределения
. Квантиль стандартного нормального распределения  может быть найден, например, по таблицам значений функции Лапласа
может быть найден, например, по таблицам значений функции Лапласа  как решение уравнения
как решение уравнения  . Здесь
. Здесь  . Подставляя в формулу данные задачи, получим:
. Подставляя в формулу данные задачи, получим:  .
.
Задание 3. Найти доверительный интервал для неизвестного математического ожидания нормально распределённой генеральной совокупности при неизвестной генеральной дисперсии с надёжностью 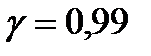 , выборочном среднем
, выборочном среднем  и выборочной дисперсии
и выборочной дисперсии 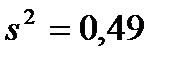 , найденных по выборке объёма
, найденных по выборке объёма  .
.
Решение. Искомый доверительный интервал имеет вид:  . Квантиль распределения Стьюдента, соответствующий надёжности
. Квантиль распределения Стьюдента, соответствующий надёжности 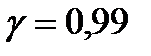 для числа степеней свободы
для числа степеней свободы 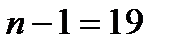 возьмём из соответствующей таблицы:
возьмём из соответствующей таблицы:  . Исправленное выборочное среднеквадратичное отклонение
. Исправленное выборочное среднеквадратичное отклонение  . Подставляя, получим:
. Подставляя, получим:  .
.
Задание 4. Для проверки эффективности новой технологии отбираются две группы рабочих. В первой группе (где она применяется) численностью 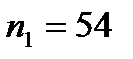 человек средняя выработка
человек средняя выработка  шт.,
шт.,  шт. Эти же показатели для другой группы (без применения новой технологии) численностью
шт. Эти же показатели для другой группы (без применения новой технологии) численностью  человека:
человека:  шт.,
шт.,  шт. На уровне значимости
шт. На уровне значимости 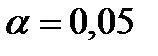 определить, действительно ли новая технология влияет на производительность.
определить, действительно ли новая технология влияет на производительность.
Решение. Для проверки гипотезы о равенстве генеральных средних двух генеральных совокупностей (новая технология не влияет на производительность) вычислим статистику:  и сравним её с
и сравним её с  - квантилью стандартного нормального распределения. Квантиль стандартного нормального распределения
- квантилью стандартного нормального распределения. Квантиль стандартного нормального распределения  может быть найден, например, по таблицам значений функции Лапласа
может быть найден, например, по таблицам значений функции Лапласа  как решение уравнения
как решение уравнения  . Подставляя, получим:
. Подставляя, получим:  . При этом
. При этом  . Так как
. Так как  , то выдвинутую гипотезу об отсутствии влияния отклоняем.
, то выдвинутую гипотезу об отсутствии влияния отклоняем.
Задание 5. При уровне значимости 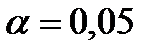 проверить гипотезу о нормальном распределении генеральной совокупности по эмпирическим и теоретическим частотам:
проверить гипотезу о нормальном распределении генеральной совокупности по эмпирическим и теоретическим частотам:
|
|
|
Таблица 8. 4

| |||||||
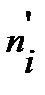
|
Решение. Необходимые вычисления проведём в таблице 8. 5.
Таблица 8.5
| № | 
| |||||||

| ||||||||

| ||||||||

| -3 | -2 | -1 | |||||

| ||||||||

| 0,09 | 0,07 | 0,21 | 0,27 | 0,67 | 0,17 | 2,47 |
Видно, что наблюдаемое значение критерия 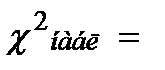 2,47. Заданному уровню значимости
2,47. Заданному уровню значимости 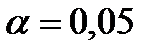 и числу степеней свободы
и числу степеней свободы  соответствует
соответствует  9,49. Так как
9,49. Так как  , то нет оснований отклонить гипотезу о нормальном распределении генеральной совокупности на данном уровне значимости.
, то нет оснований отклонить гипотезу о нормальном распределении генеральной совокупности на данном уровне значимости.
Задание 6. По данным корреляционной таблицы 8. 6 построить выборочные уравнения регрессии.
Таблица 8.6
Себестоимость, у.е. 
| Производительность труда, 
| 
| ||||
|
Решение. Уравнение регрессии “  на
на  ”:
”:  , “
, “  на
на  ”:
”:
 .
.
Для удобства выпишем распределения составляющих:
Таблица 8. 7

| |||||

| |||||
| Таблица 8.8 | |||||
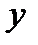
| |||||

|
По таблицам 8.7 и 8.8 рассчитаем  14,95,
14,95,  228,
228,  4,50,
4,50, 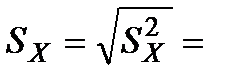 2,12,
2,12,  11,05,
11,05,  126,8,
126,8,  4,70,
4,70,  2,17,
2,17,  6472,
6472,
 161,8,
161,8,  -3,40,
-3,40,  -0,74,
-0,74,  -0,76;
-0,76;  -0,72.
-0,72.
Тогда уравнение регрессии “  на
на  ”:
”:  , “
, “  на
на  ”:
”:  .
.
|
|
|


