 |
Знания на уровне понятий, определений, формулировок, описаний.
|
|
|
|
1. Генеральная и выборочная совокупность, частота варианты, относительная частота варианты.
2. Выборки повторные и безповторные. Репрезентативность выборки. Статистическое распределение выборки, вариационный ряд.
3. Теоретическая и эмпирическая функции распределения.
4. Графическое представление выборки: полигон и гистограмма.
5. Числовые характеристики выборки: выборочная средняя, выборочная дисперсия и исправленная выборочная дисперсия, выборочное среднее квадратическое отклонение и исправленное выборочное среднее квадратическое отклонение, выборочная мода, выборочная медиана, эмпирические начальные и центральные моменты различных порядков.
6. Точечные оценки неизвестных параметров генеральной совокупности. Метод моментов и метод максимального правдоподобия получения точечных оценок.
7. Интервальные оценки неизвестных параметров генеральной совокупности: доверительный интервал, доверительная вероятность
8. Требования, предъявляемые к оценкам: несмещённость, эффективность, состоятельность.
9. Доверительный интервал для неизвестного математического ожидания нормально распределённой генеральной совокупности при известной генеральной дисперсии.
10. Доверительный интервал для неизвестного математического ожидания нормально распределённой генеральной совокупности при неизвестной генеральной дисперсии.
11. Доверительный интервал для неизвестного среднеквадратического отклонения нормально распределённой генеральной совокупности.
12. Понятие статистической гипотезы. Гипотезы простые и сложные, параметрические и непараметрические. Нулевая гипотеза, альтернативная гипотеза, ошибки первого и второго рода.
|
|
|
13. Уровень значимости и мощность критерия.
14. Методика проверки статистической гипотезы. Статистический критерий, область принятия решения, критическая область, критическая точка, односторонние и двусторонние критические области.
15. Проверка гипотезы о равенстве генерального среднего конкретному значению.
16. Проверка гипотезы о равенстве генеральных средних двух генеральных совокупностей
17. Проверка гипотезы о равенстве дисперсий двух генеральных совокупностей.
18. Критерии согласия: 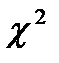 Пирсона и Колмогорова.
Пирсона и Колмогорова.
19. Зависимости функциональные, статистические и корреляционные.
20. Линейная регрессия случайных величин 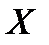 и
и 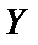
21. Выборочный коэффициент корреляции. Проверка гипотезы о наличии или отсутствии зависимости между случайными величинами с помощью выборочного коэффициента корреляции
22. Прямые линейной эмпирической регрессии “ 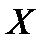 на
на 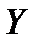 ” и “
” и “ 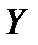 на
на  ”.
”.
Знания на уровне доказательств и выводов:
1. Построение доверительного интервала для неизвестного математического ожидания нормально распределённой генеральной совокупности при известной генеральной дисперсии.
2. Построение доверительного интервала для неизвестного математического ожидания нормально распределённой генеральной совокупности при неизвестной генеральной дисперсии.
Умения в решении задач
1. Строить полигон и гистограмму по выборке
2. Строить эмпирическую функцию распределения и её график по выборке
3. Вычислять числовые характеристики выборки: выборочную среднюю, выборочную дисперсию и исправленную выборочную дисперсию, выборочное среднее квадратическое отклонение и исправленное выборочное среднее квадратическое отклонение, выборочную моду, выборочную медиану.
4. Строить доверительный интервал для неизвестного математического ожидания нормально распределённой генеральной совокупности при известной генеральной дисперсии
|
|
|
5. Строить доверительный интервал для неизвестного математического ожидания нормально распределённой генеральной совокупности при неизвестной генеральной дисперсии
6. Проверять гипотезу о равенстве генеральных средних двух генеральных совокупностей
7. Проверять гипотезу о равенстве дисперсий двух генеральных совокупностей.
8. Проверять гипотезу о законе распределения по критерию согласия 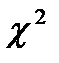 .
.
9. По данным двумерной выборки строить эмпирическую простую линейную регрессию.
|
|
|


