Подсчет критерия тенденций L Пейджа

1.Проранжировать индивидуальные значения первого испытуемого, полученные им в 1-м, 2-м, 3-ми т. д. замерах.

При этом первым может быть любой испытуемый, например пер­вый по алфавиту имен.

2.Проделать то же самое по отношению ко всем другим испытуемым.

3.Просуммировать ранги по условиям, в которых осуществлялись за­меры. Проверить совпадение общей суммы рангов с расчетной сум­мой.

4.Расположить все условия в порядке возрастания их ранговых сумм в таблице.

5.Определить эмпирическое значение L по формуле:

где T_i - сумма рангов по данному условию;

j - порядковый номер, приписанный данному условию в упоря­доченной последовательности условий.

6. По Taбл.VIII определить критические значения L для данного количества испытуемых п и данного количества условий с. Если L_эмп ≥ критическому значению, тен­денция достоверна.

Таблица VIII. Критические значения критерия тенденций L Пейджа для количества

условий от трех до шести (3≤с≤6) и количества испытуемых от двух до двенадцати (2≤n≤12).

n	с (количество условий)
				Р
	– –	–			0,001 0,01 0,05
	–				0,001 0,01 0,05
					0,001 0,01 0,05
					0,001 0,01 0,05
					0,001 0,01 0,05
					0,001 0,01 0,05
					0,001 0,01 0,05
					0,001 0,01 0,05
					0,001 0,01 0,05
					0,001 0,01 0,05
					0,001 0,01 0,05

 

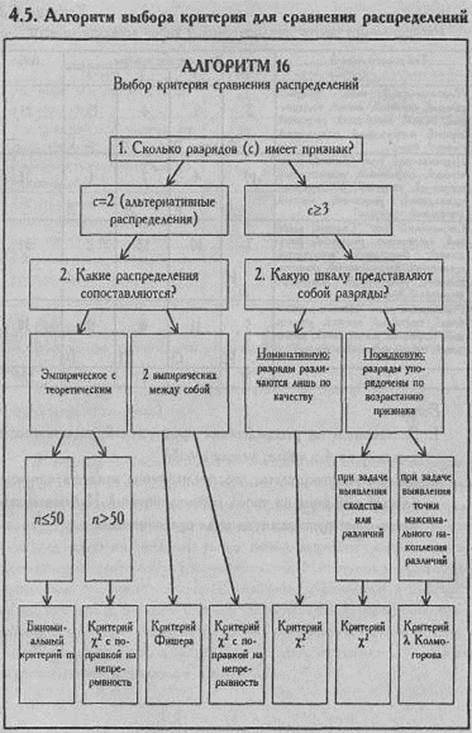
ГЛАВА IV. ВЫЯВЛЕНИЕ РАЗЛИЧИЙ В РАСПРЕДЕЛЕНИИ ПРИЗНАКА

χ² критерий Пирсона

Назначения критерия. Критерий χ² применяется в двух целях:

1) для сопоставления эмпирического распределения признака с теоре­тическим - равномерным, нормальным или каким-то иным;

2) для сопоставления двух, трех или более эмпирических распределе­ний одного и того же признака.

 

Шутливый пример

В гениальной комедии Н. В. Гоголя "Женитьба" у купеческой дочери Агафьи Тихоновны было пятеро женихов. Одного она сразу исключила из рассмотрения, потому что он был купеческого звания, как и она сама. А из остальных она не знала, кого выбрать: "Уж как труд­но решиться, так просто рассказать нельзя, как трудно. Если бы губы Никанора Ивановича да приставить к носу Ивана Кузьмича, да взять сколько-нибудь развязности, какая у Балтазара Балтазарыча, да, пожа­луй, прибавить к этому еще дородности Ивана Павловича, я бы тогда тотчас решилась. А теперь поди подумай! просто голова даже стала болеть. Я думаю, лучше всего кинуть жребий". И вот Агафья Тихоновна положила бумажки с четырьмя имена­ми в ридикюль, пошарила рукою в ридикюле и вынула вместо одного — всех!

Ей хотелось, чтобы жених совмещал в себе достоинства всех чет­верых, и, вынимая все бумажки вместо одной, она бессознательно со­вершала процедуру выведения средней величины. Но вывести среднюю величину из четверых людей невозможно, и Агафья Тихоновна в смя­тении. Она влюблена, но не знает, в кого. "Такое несчастное положе­ние девицы, особливо еще влюбленной".

Вся беда в том, что ни Агафья Тихоновна, ни ее тетушка, ни сваха Фекла Ивановна не были знакомы с критерием χ2! Именно он мог бы им помочь в решении их проблемы. С его помощью можно бы­ло бы попробовать установить, в кого больше влюблена Агафья Тихо­новна. Но для этого нам не нужно измерять губы Никанора Ивановича или нос Ивана Кузьмича, или объем талии дородного экзекутора Ива­на Павловича; не нужно нам и пускаться на какие-нибудь опасные экс­перименты, чтобы определить, насколько далеко простирается развяз­ность Балтазара Балтазарыча. Мы эти их достоинства принимаем как данность потому лишь, что они нравятся Агафье Тихоновне. Мы при­нимаем их за разряды одного и того же признака, например, направ­ленности взгляда Агафьи Тихоновны: сколько раз она взглянула на губы Никанора Ивановича? На нос Ивана Кузьмича? Благосклонно взирала на дородного Ивана Павловича или развязного Балтазара Балтазаровича? Внимательная сваха или тетушка вполне могла бы этот признак наблюдать. Допустим, за полчаса смотрин ею зафиксированы следующие наблюдения.

Агафья Тихоновна:

сидела с опущенными глазами 25 минут;

благосклонно смотрела на Никанора Ивановича 14 раз;

благосклонно смотрела на Ивана Кузьмича 5 раз;

благосклонно смотрела на Ивана Павловича 8 раз;

благосклонно смотрела на Балтазара Балтазарыча 5 раз.

 

 

АЛГОРИТМ 13

Расчет критерия χ2

1. Занести в таблицу наименования разрядов и соответствующие им эмпирические частоты (первый столбец).

2. Рядом с каждой эмпирической частотой записать теоретическую частоту (второй столбец).

3. Подсчитать разности между эмпирической и теоретической частотой по каждому разряду (строке) и записать их в третий столбец.

4. Определить число степеней свободы по формуле:

ν=κ-1

где κ - количество разрядов признака.

Если ν = 1, внести поправку на «непрерывность».

5. Возвести в квадрат полученные разности и занести их в четвертый столбец.

6. Разделить полученные квадраты разностей на теоретическую частоту и записать результаты в пятый столбец.

7. Просуммировать значения пятого столбца. Полученную сумму обозначить как χ²_эмп.

8. Определить по Табл. IX критические значения для данного числа степеней свободы ν.

Если χ²_эмп < критического значения, расхождения между распределениями статистически недостоверны.

Если χ²_эмп ≥ критическому значению, расхождения между распределениями статистически достоверны.

Таблица IX. Критические значения критерия χ² для уровней

статистической значимости р≤0,05 и р≤0,01 при разном числе степеней свободы ν.

 

ν	Р	ν	Р	ν	Р
0,05	0,01	0,05	0,01	0,05	0,01
	3,841	6,635		49,802	57.342		89.391	99,227
	5,991	9.210		50,998	58.619		90.631	100,425
	7,815	11,345		52,192	59,892		91,670	101,621
	9,488	13.277		53,384	61,162		92,808	102,816
	11,070	15.086		54,572	62.428		93,945	104,010
	12,592	16,812		55,758	63,691		95,081	105,202
	14,067	18,475		56,942	64,950		96,217	106,393
	15,507	20.090		58,124	66,206		97,351	107,582
	16,919	21,666		59,304	67,459		98,484	108,771
	18,307	23,209		60,481	68,709		99,617	109,958
	19,675	24,725		61,656	69,957		100,749	111,144
	21,026	26,217		62,830	71,201		101,879	112,329
	22.362	27,688		64,001	72,443		103,010	113,512
	23,685	29,141		65,171	73,683		104,139	114,695
	24,996	30,578		66,339	74,919		105,267	115,876
	26,296	32,000		67,505	76,154		106,395	117,057
	27,587	33,409		68.669	77,386		107,522	118,236
	28,869	34,805		69.832	78,616		108,648	119,414
	30,144	36,191		70,993	79,843		109.773	120,591
	31,410	37,566		72,153	81,069		110.898	121,767
	32,671	38,932		73,311	82,292		112,022	122,942
	33.924	40.289		74,468	83,513		113,145	124,116
	35,172	41.638		75.624	84,733		114,268	125,289
	36.415	42.980		76.778	85,950		115,390	126,462
	37,652	44,314		77,931	87,166		116.511	127,633
	38,885	45,642		79.082	88,379		117,632	128,803
	40,113	46.963		80.232	89.591		118,752	129,973
	41,337	48,278		81.381	90,802		119,871	131.141
	42.557	49,588		82.529	92,010		120,990	132,309
	43,773	50.892		83,675	93,217		122,108	133,476
	44,985	52,191		84.821	94,422		123,225	134,642
	46,194	53.486		85,965	95,626		124,342	135,807
	47,400	54.776		87,108	96,828
	48,602	56.061		88,250	98,028

 

λ - критерий Колмогорова-Смирнова

Назначение критерия. Критерий X предназначен для сопоставления двух распределений: а) эмпирического с теоретическим, например, равномерным или
нормальным; б) одного эмпирического распределения с другими эмпирическим
распределением. Критерий позволяет найти точку, в которой сумма накопленных расхождений между двумя распределениями является наибольшей, и оценить достоверность этого расхождения.

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: