Сопоставление эмпирического распределения с теоретическим

Пример 1.

Ввыборке здоровых лиц мужского пола, студентов технических и военно-технических вузов в возрасте от 19-ти до 22 лет, средний воз­раст 20 лет, проводился тест Люшера в 8-цветном варианте. Установ­лено, что желтый цвет предпочитается испытуемыми чаще, чем отверга­ется (Табл. 4.16). Можно ли утверждать, что распределение желтого цвета по 8-и позициям у здоровых испытуемых отличается от равно­мерного распределения?

 

АЛГОРИТМ 14

Расчет абсолютной величины разности d между эмпирическим и равномерным распределениями

1.Занести в таблицу наименования разрядов и соответствующие им
эмпирические частоты (первый столбец).

2. Подсчитать относительные эмпирические частоты (частости) для
каждого разряда по формуле:

f *_эмп= f _эмп/ n

где f _эмп - эмпирическая частота по данному разряду;

п - общее количество наблюдений. Занести результаты во второй столбец.

3. Подсчитать накопленные эмпирические частости Σ f *j по формуле:

где Σ f *j=Σ f *_j-1+ f *_j - частость, накопленная на предыдущих разрядах; j - порядковый номер разряда; f*_j- эмпирическая частость данного /-го разряда. Занести результаты в третий столбец таблицы.

4. Подсчитать накопленные теоретические частости для каждого раз­
ряда по формуле:

Σ f *_{т j}=Σ f *_{Т j-1}+ f *_{т j} где Σ f *_{т j-1} - теоретическая частость, накопленная на предыдущих

разрядах;

j - порядковый номер разряда;

f *_{т j} - теоретическая частость данного разряда. Занести результаты в третий столбец таблицы.

5. Вычислить разности между эмпирическими и теоретическими нако­
пленными частостями по каждому разряду (между значениями 3-го
и 4-го столбцов).

6. Записать в пятый столбец абсолютные величины полученных раз­
ностей, без их знака. Обозначить их как d.

7. Определить по пятому столбцу наибольшую абсолютную величину
разности - d_max.

8. По Табл. X определить или рассчитать критические
значения d_max для данного количества наблюдений n.

Если d_max ≥ критическому значению d, различия между распределениями достоверны.

Таблица X. Критические значения d_max, соответствующие уровням статистической значимости р≤0,05 и р≤0,01 при сопоставлении эмпирического распределения с теоретическим.

 

п	Максимальный модуль разности накопленных частостей dmax,	п	Максимальный модуль разности накопленных частостей dmax
р=0,05	р=0,01	р=0,05	р=0,01
	0,6074	0,7279		0,1921	0,2302
	0,4295	0,5147		0,1753	0,2101
	0.3507	0,4202		0,1623	0,1945
	0,3037	0,3639		0,1518	0,1820
	0,2716	0,3255		0,1432
	0,2480	0,2972		0,1358
	0,2147	0,2574	>100	1,36/√n	1,63/√n

Сопоставление двух эмпирических распределений

Пример 2.

Интересно сопоставить данные, полученные в предыдущем при­мере, с данными обследования X. Кларом 800 испытуемых. X. Кларом было показано, что желтый цвет является единственным цветом, распределение которого по 8 позициям не отли­чается от равномерного.

АЛГОРИТМ 15

Расчет критерия λ при сопоставлении двух эмпирических распределений

1. Занести в таблицу наименования разрядов и соответствующие им эмпирические
частоты, полученные в распределении 1 (первый столбец) и в распределении 2
(второй столбец).

2. Подсчитать эмпирические частости по каждому разряду для распределения 1
по формуле:

f *_э= f _э/ n ₁

где f _э - эмпирическая частота в данном разряде;

п ₁ - количество наблюдений в выборке. Занести эмпирические частости распределения 1 в третий столбец.

3. Подсчитать эмпирические частости по каждому разряду для распределения 2
по формуле:

f *_э= f _э/ n ₂

где f _э - эмпирическая частота в данном разряде;

n₂ - количество наблюдений во 2-й выборке.

Занести эмпирические частости распределения 2 в четвертый столбец таблицы.

4. Подсчитать накопленные эмпирические частости для распределения 1 по формуле:

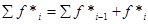
где Σ f *_j-1 - частость, накопленная на предыдущих разрядах;

j - порядковый номер разряда;

f* _j-1 - частость данного разряда.

Полученные результаты записать в пятый столбец.

5. Подсчитать накопленные эмпирические частости для распределения 2 по той
же формуле и записать результат в шестой столбец.

6. Подсчитать разности между накопленными частостями по каждому разряду.
Записать в седьмой столбец абсолютные величины разностей, без их знака.
Обозначить их как d.

7. Определить по седьмому столбцу наибольшую абсолютную величину разности

8. Подсчитать значение критерия λ по формуле:

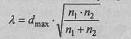
где п ₁ - количество наблюдений в первой выборке;

n ₂ - количество наблюдений во второй выборке.

9. По Табл. XI определить, какому уровню статистической значимости соответствует полученное значение λ.

Если λ_эмп > 1,36, различия между распределениями достоверны.

Таблица XI. Критерий λ Колмогорова-Смирнова для сопоставления эмпирического распределения с теоретическим (при n>50) или двух эмпирических распределений между собой (при n>50): уровни статистической значимости разных значений λ_эмп. По полученному значению λ_эмп определяется уровень значимости различий между двумя распределениями.

X	λ, последний десятичный знак
р - десятичные знаки («0», опущен)
0,3
0,4
0.5
0.6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: