Задание 4.1. Таблица 4.1. Численность родившихся в расчете на 1000 населения, чел. (Хi )

Задание 4. 1

По данным о числе родившихся в РФ (табл. 2. 1. задание 2. 2) определите средний уровень рождаемости за представленные годы и показатели вариации. Для расчетов используйте таблицу:

Таблица 4. 1

Расчет показателей вариации рождаемости

Годы	Численность родившихся в расчете на 1000 населения, чел. (Хi )	Расчет отклонений
		|Хi-	(Хi-2
	10, 4
	10, 2
	10, 4
	11, 3
	12, 1
	12, 4
	12, 5
Итого
В среднем

 

Задание 4. 2.

Определите по сгруппированным данным:

· Средний возраст студентов

· абсолютные, средние и относительные показатели вариации возраста студентов

 

Таблица 4. 2

Распределение студентов по возрасту

Исходные данные		Расчетные показатели
Группы студентов по возрасту, лет Xi	Число студентов fi	Xi fi	Xi-	|Xi-| fi	(Xi-)2 fi
	fi
Итого

Определите:

· Средний возраст студентов

· абсолютные, средние и относительные показатели вариации возраста студентов

 

 

Задание 4. 2

Охарактеризуйте ряд распределения. Определите дисперсию, среднее квадратическое отклонение и коэффициент вариации

Таблица 4. 2

Распределение работников отрасли по уровню заработной платы

Заработная плата одного работника за месяц, тыс. руб.	До 15	15-20	20-30	30 и больше	Всего
Количество работников к итогу, %

Задание 4. 3

Сравните вариацию производительности труда в цехах, сделайте выводы.

Таблица 4. 3

Цех	Средняя часовая производительность труда в цехе, м2	Среднее отклонение часовой производительности каждого работника от среднецеховой производительности, м2
		0, 36 0, 8 2, 45

Задание 4. 4

Дисперсия признака равна 10, средний квадрат его индивидуальных значений – 140. Чему равна средняя?

Задание 4. 5

Средняя величина признака в совокупности равна 20, а средний квадрат отклонений индивидуальных значений этого признака от средней величины – 400. Определите коэффициент вариации.

Задание 4. 6

Средняя величина в совокупности равна 16, среднее квадратическое отклонение – 8. Определите средний квадрат индивидуальных значений этого признака.

Задание 4. 7

Имеются данные о производительности в двух группах, сформированных по величине стажа работы:

Таблица 4. 4

Производительность ткачей в двух бригадах

Табельный номер	Изготовлено ткани за 1 час, м. ( Хi)	(Хi-гр)2	(Хi-)2
1 группа (стаж от 1 до 3 лет):
Итого 1 гр. (бригаде)
В среднем по 1 гр ()		х	х
2 группа (стаж свыше 3 лет):
Итого 2 гр. (бригаде)
В среднем по 2 гр ()		х	х
Всего
В среднем ()		х	х

Вычислить:

· групповые дисперсии и среднюю из групповых дисперсий (внутригрупповую);

 

· межгрупповую дисперсию;

 

 

· общую дисперсию.

 

 Проверить правило сложения дисперсий.

Определить коэффициент вариации в двух бригадах.

Задание 4. 8

Имеются данные о товарообороте магазинов

Таблица 4. 5

Распределение магазинов по размеру товарооборота

Группы магазинов по размеру товарооборота, тыс. руб.	Число магазинов fi	Середина интервала Xi	Xifi	Xi-	(Xi-)2fi	(Xi-)4fi
50-60 60-70 70-80 80-90
Итого		х

Исходя их данных о распределении магазинов по размеру товарооборота определите следующие показатели и сделайте выводы:

· средний размер товарооборота по магазинам

 

 

· Дисперсию (центральный момент второго порядка)

 

 

· Среднее квадратическое отклонение;

 

 

· Моду

 

 

· Коэффициент асимметрии Пирсона

 

· Центральный момент четвертого порядка

· Нормированный момент четвертого порядка

 

· Эксцесс распределения

 

 

Тема 5: Статистическое изучение взаимосвязей социально-экономических явлений

 

Взаимосвязи между явлениями могут быть функциональными (математическими) и стохастическими (корреляционными).

Основные методы изучения взаимосвязей:

· метод сопоставления параллельных рядов,

· балансовый,

· графический,

· метод аналитических группировок,

· дисперсионный анализ;

·  Корреляционно-регрессионный анализ (КРА).

Цель корреляционного анализа – определить форму связи с помощью подбора уравнения зависимости. Прямолинейная зависимость в этом случае может быть выражена уравнением прямой:

 

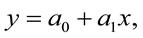
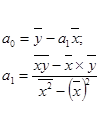Для нахождения параметров можно воспользоваться формулами:

 

Цель регрессионного анализа – оценить тесноту связи. Теснота связи оценивается с помощью коэффициентов корреляции, корреляционного отношения, детерминации, эластичности и др.

Парный линейный коэффициент корреляции:

,

где - средние квадратические отклонения по факторному признаку X (результативному У):

 

Если же связь криволинейная, то пользуются корреляционным отношением (индексом корреляции):

 

где - выравненные значения по уравнению регрессии.  

 

Студент должен

знать:

· виды и формы взаимосвязей;

· сущность функциональных и корреляционных взаимосвязей между показателями;

· основные методы для определения взаимосвязи между показателями;

· методику расчета коэффициентов тесноты связи

уметь:

· Определять признак-фактор и признак-результат;

· Пользоваться основными методами для определения направления и тесноты связи явлений.

· Оценивать достоверность полученных результатов;

· Интерпретировать полученные данные.  

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: